Расчет и нанесение уклона на обмерных чертежах
С необходимостью посчитать уклон постоянно сталкиваются проектировщики, строители, архитекторы, а также люди ряда других профессий, в силу того, что на земной поверхности очень трудно найти идеально ровный участок. Уклон выражается в градусах или в процентах. Обозначение в градусах показывает угол кривизны поверхности. Но уклон может быть представлен и в виде тангенса этого угла, умноженного на 100%.
Как рассчитать уклон поверхности?
Уклон – это отношение превышения (ВС) к заложению (АС) и обозначается в текстовых документах буквой i.
Например, i=1:6
Разделите противолежащий катет (вертикальное расстояние) на прилежащий (расстояние между точками). Если вам нужно получить уклон в процентах, умножьте полученное число на 100%. Чтобы получить уклон в промилле, умножьте результат деления на 1000‰.
Если вам необходимо получить уклон в градусах, воспользуйтесь тем, что полученный при делении катетов результат – тангенс угла наклона.
На видах (фасадах), разрезах, сечениях и схемах перед размерным числом, определяющим величину уклона, наносят знак , острый угол которого должен быть направлен в сторону уклона.
Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.
На планах направление уклона плоскостей указывают стрелкой, на которой, при необходимости, проставляют величину уклона (см.рис.).
Построение и обозначение уклона. Пример изображения уклона на планах.
Величину уклона (тангенс угла наклона) указывают в виде простой или десятичной дроби с точностью до третьего знака.
Уклон (в строительстве) — показатель крутизны склона (а также ската кровли).
Укло́н (в геодезии) — показатель крутизны склона; отношение превышения местности к горизонтальному проложению, на котором оно наблюдается. Иными словами, величина уклона равна тангенсу угла между поверхностью склона и горизонталью.
Уклон поверхности равен тангенсу угла α, tgα = h/l — отношение перпендикуляра, опущенного из точки поверхности на прямую поверхность, к длине прямой поверхности от начала склона (при вершине угла α) до перпендикуляра.
Например, подъёму 12 м на 100 м перемещения по горизонтали соответствует уклон, равный 0,12 (12 % или 120 ‰).
При чтении нотации знак «%» произносится «сотых», а «‰» — «тысячных».
Источник:
книга: Единые требования по выполнению строительных чертежей.
М.: Изд-во «Архитектура-С», 2004.
Справочное пособие.
Автор: Георгиевский О.В.
Аннотация:
Справочное пособие по строительному черчению для студентов средних и высших учебных заведений. Пособие выполнено в соответствии с требованиями ГОСТов.
Настоящее справочное пособие выполнено в соответствии с требованиями ГОСТов ЕСКД (Единой системы конструкторской документации) и СПДС (Системы проектной документации для строительства).

Распечатать
Вконтакте
Одноклассники
Google+
Уклоны. Теория — на уровне глаз — ЖЖ
Как было сказано ранее, по одному из определений уклон это тангенс угла. С большим интересом узнал, что он равен коэффициенту сцепления. Вот тут и начинает прояснятся тайный смысл предупреждающих дорожных знаков 1.13 и 1.14 (крутой спуск / подъём).
Коэффициентом сцепления называется отношение двух сил – силы, необходимой для сдвига машины с заблокированными колесами, и силы тяжести, прижимающей машину к дороге. Так мы легко можем получить коэффициенты сцепления для сухого асфальта – 7000/10000 = 0,7, для грязной дороги – 3000/10000 = 0,3, и для льда – 1000/10000 = 0,1.
Например, автомобиль, стоящий на сухом асфальтированном уклоне с коэффициентом сцепления 0,7, начнет сползать вниз, если тангенс угла наклона при этом будет равен 70% (это уклон около 35 градусов, вряд ли вы когда-нибудь встретите такой). Но, кроме дорог, существуют улочки старых городов, особенно приморских, с углами наклона, существенно превышающими всевозможные нормативы. [2]
Но, кроме дорог, существуют улочки старых городов, особенно приморских, с углами наклона, существенно превышающими всевозможные нормативы. [2]
К тому же, «при движении в сырую погоду вниз по асфальтированному уклону крутизной 20% эффективность торможения падает наполовину. И очень часто вам придется двигаться по мокрому льду с коэффициентом сцепления 0,1 и менее. А это значит, что вы должны внимательно отслеживать предупреждающие дорожные знаки 1.13 и 1.14. Их устанавливают, когда тангенс угла уклона приближается к 10%. Если вы пренебрежете этими знаками и остановитесь на подъеме, то в лучшем случае – не сможете сдвинуться с места. А уж если затормозите на спуске, машину может занести. Старайтесь тормозить двигателем на длительных спусках.» [2]
Вот о чём предупреждают знаки.
Кстати, есть знаки и меньше 10%, поэтому стало интересно в каких случаях их устанавливают.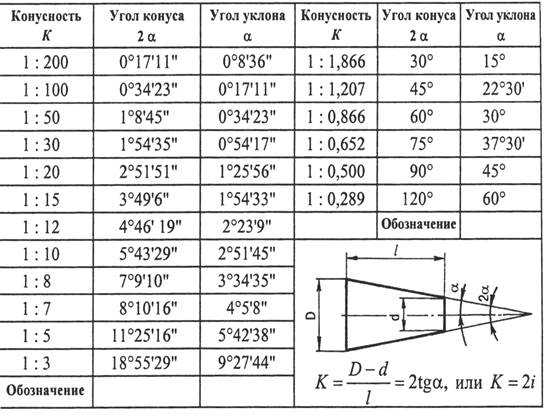
ГОСТ Р 52289-2004 «Правила применения дорожных знаков, разметки, светофоров, дорожных ограждений и направляющих устройств», п. 5.2.16:
4% — если длина участка дороги на спуске или подъёме больше 600 метров при данном уклоне.
5% если больше 450 метров
6% если больше 350 метров
7% если больше 300 метров
8% (и более) если больше 270 метров.
Там же указаны и другие случаи, как например расстояние видимости, но сейчас они нас не интересуют.
Причины: почему проценты?
При рассмотрении темы уклонов всегда возникает вопрос, а почему уклон измеряют в процентах, а не в привычных градусах? По этому поводу слышал несколько версий:
а) КартыТак проще вычислять уклон рельефа на карте или на строительном плане. Рельеф на картах обозначается линиями — горизонталями. Это замкнутая линия, которая получается если мысленно сделать сечение на какой-либо высоте и посмотреть сверху. Проще это представить если вспомнить линию уреза воды реки или водоёма, это тоже своего рода горизонталь.

Горизонтали, т.е. горизонтальные сечения, проводятся через определённое постоянное расстояние по высоте, о чём указывается в примечаниях. Зная высоту сечения горизонталей и определив на карте расстояние между ними можно получить уклон. Чем ближе друг к другу на карте изображены горизонтали, тем рельеф круче.
б) Погрешность
Построить угол, заданный в градусах, так сказать «в натуре» на строительной площадке, задача не из простых, а построить точно и вовсе запредельная. Небольшие величины уклона в градусах имеют вид десятичных дробей, а ведь погрешность даже в 1° на 10 метров длины даст ошибочные 17 сантиметров высоты. Так же, проценты величина относительная, и потому уклон, выраженный в процентах, можно построить имея в распоряжении только рулетку (или иной инструмент для измерения длинны) и уровень.
в) Неравномерность
Дорога, на протяжении всего спуска (подъёма), имеет неравномерный уклон. В каждый отдельный момент угол разный, и поэтому проще посчитать сколько составляет горизонтальная длинна участка спуска (подъёма), и на сколько изменилась высота относительно начала спуска (подъёма).
seyfulmulyukov.livejournal.com / 1avtorul.ru
Все эти версии вполне имеют право на жизнь. Общим для них является то, что для нахождения величины уклона используются меры длинны, которые всегда есть под рукой, а это практично. Что касается дорожных знаков, то более правдоподобной выглядит третья версия (неравномерность уклона), а для строительства дорог вторая (погрешность построений).
Есть ещё Международная Конвенция о дорожных знаках и сигналах за 1968 год, и Европейское соглашение 1971 года, дополняющее эту Конвенцию, по которой на предупреждающих знаках крутизна уклонов и подъемов указывается в процентах. [3]
Что стоит за цифрами, например 1/12 или 10%, много это или мало, как это выглядит и где применяется, рассмотрим в следующий раз на примерах из жизни.
Использованные материалы
1. Словари и энциклопедии на Академике © Академик2. Материалы сайта «Школа жизни» © Shkolazhizni.ru
3.
 Википедия © Wikipedia
Википедия © Wikipedia—
Как начертить уклоны и конусность
Во многих деталях машин используются уклоны и конусность. Уклоны встречаются в профилях прокатной стали, в крановых рельсах, в косых шайбах и т. д. Конусности встречаются в центрах бабок токарных и других станков, на концах валов и ряда других деталей.
Уклон характеризует отклонение прямой линии от горизонтального или вертикального направлений. Для того чтобы построить уклон 1:1, на сторонах прямого угла откладывают произвольные, но равные величины (рис. 1). Очевидно, что уклон 1:1 соответствует углу в 45 градусов. Чтобы построить линию с уклоном 1:2, по горизонтали откладывают две единицы, для уклона 1:3 — три единицы и т. д. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а. Величину уклона на чертеже в соответствии с ГОСТ 2.307—68 указывают с помощью линии-выноски, на полке которой наносят знак уклона и его величину.
На рисунке в качестве примера построен профиль несимметричного двутавра, правая полка которого имеет уклон 1:16. Для ее построения находят точку А с помощью заданных размеров 26 и 10. В стороне строят линию с уклоном 1:16, для чего по вертикали откладывают, например, 5 мм, а по горизонтали 80 мм; проводят гипотенузу, направление которой определяет искомый уклон. С помощью рейсшины и угольника через точку А проводят линию уклона, параллельную гипотенузе.
Конусностью называют отношение диаметра основания конуса к его высоте. В этом случае конусность К=d/l. Для усеченного конуса К = (d-d1)/l. Пусть требуется построить конический конец вала по заданным размерам: d — диаметр вала — 25 мм; I — общая длина конца вала — 60 мм; l1 — длина конической части — 42 мм; d1 — наружный диаметр резьбы — 16 мм; К — конусность 1 : 10 (рис. 3, б). Прежде всего, пользуясь осевой, строят цилиндрическую часть вала, имеющую диаметр 25 мм. Этот размер определяет также большее основание конической части. После этого строят конусность 1:10. Для этого строят конус с основанием, равным 10 мм, и высотой, равной 100 мм (можно было бы воспользоваться и размером 25 мм, но в этом случае высота конуса должна быть взята равной 250 мм, что не совсем удобно). Параллельно линиям найденной конусности проводят образующие конической части вала и ограничивают ее длину размером 42 мм. Как видно, размер меньшего основания конуса получается в результате построения. Этот размер обычно не наносят на чертеж. Запись М16X1,5 является условным обозначением метрической резьбы, о чем подробнее будет сказано дальше.
3, б). Прежде всего, пользуясь осевой, строят цилиндрическую часть вала, имеющую диаметр 25 мм. Этот размер определяет также большее основание конической части. После этого строят конусность 1:10. Для этого строят конус с основанием, равным 10 мм, и высотой, равной 100 мм (можно было бы воспользоваться и размером 25 мм, но в этом случае высота конуса должна быть взята равной 250 мм, что не совсем удобно). Параллельно линиям найденной конусности проводят образующие конической части вала и ограничивают ее длину размером 42 мм. Как видно, размер меньшего основания конуса получается в результате построения. Этот размер обычно не наносят на чертеж. Запись М16X1,5 является условным обозначением метрической резьбы, о чем подробнее будет сказано дальше.
n
n
TBegin—>TEnd—>
n
n
Рис. 1. Построение уклонов
n
n
Перед размерным числом, характеризующим конусность, наносят условный знак в виде равнобедренного треугольника, вершину которого направляют в сторону вершины самого конуса. Знак конусности располагают параллельно оси конуса над осью или на полке линии-выноски, заканчивающейся стрелкой, как в случае надписи уклона. Конусность выбирают в соответствии с ГОСТ 8593—57 .
Знак конусности располагают параллельно оси конуса над осью или на полке линии-выноски, заканчивающейся стрелкой, как в случае надписи уклона. Конусность выбирают в соответствии с ГОСТ 8593—57 .
n
n
n
n
Рис. 2. Пример построения уклонов
n
n
TBegin—>TEnd—>
n
n
Рис. 3. Построение конусности
n
Как узнать уклон крыши в градусах
как узнать угол наклона ската в градусах, как рассчитать угол стропил двухскатной крыши, узнать и высчитать
Содержание:
Чтобы крыша здания могла в полной мере выполнять все возложенные на нее функции, необходимо при ее создании учесть ряд параметров. Одним из самых важных параметров крыши является ее уклон, который обеспечивает отвод атмосферных осадков с ее поверхности и влияет на способность выдерживать внешние нагрузки. О том, как посчитать наклон крыши, и пойдет речь в данной статье.
Определение наклона крыши — от чего зависит
Чтобы провести правильный расчет уклона крыши, необходимо учитывать несколько факторов, среди которых сильнее всего выделяются следующие:
- Ветровые нагрузки. На уклон скатов очень сильно влияет ветер. Чтобы крыша могла нормально сопротивляться его воздействию, нужно правильно подобрать ее угол. При слишком больших углах нагрузка на них будет высокой, но чрезмерное уменьшение угла тоже может быть опасным – пологую кровлю сильным порывом ветра может попросту сорвать.
- Снеговые и дождевые нагрузки

Отталкиваясь от этих факторов, можно рассчитывать угол наклона скатов. Кроме того, перед тем, как рассчитать угол двухскатной крыши, стоит обратить внимание на рекомендуемые показатели: для местности с сильными ветрами подойдет уклон в 15-20 градусов, а в остальных случаях оптимальная величина уклона составляет 35-40 градусов. Разумеется, нужно понимать, что расчет двухскатной крыши индивидуален, и выбирать усредненные показатели просто так нежелательно.
Методика проведения расчетов
При проектировании крыши нужно в обязательном порядке проводить ряд расчетов, среди которых всегда должен присутствовать расчет угла наклона скатов. Данный параметр напрямую влияет на конструкцию крыши: при увеличении наклона снижается снеговая нагрузка, но увеличивается воздействие ветра, поэтому стропильную систему приходится дополнительно усиливать. Для обустройства скатов под большим углом требуется еще и большее количество материалов, что негативно сказывается на стоимости строительства.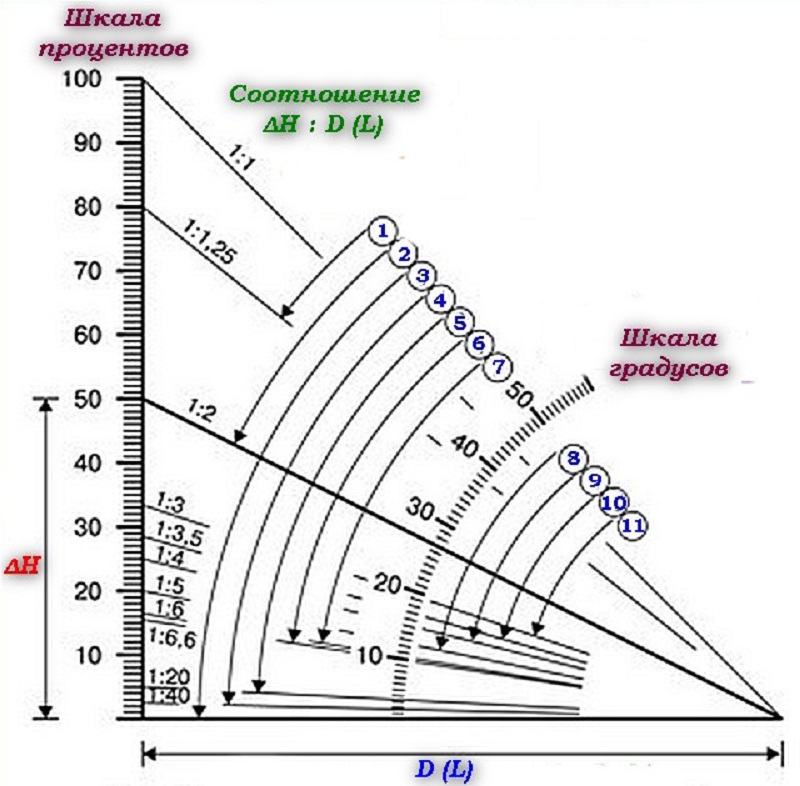
Перед тем, как узнать градус наклона крыши, нужно рассчитать эксплуатационную нагрузку на крышу, для чего требуется два параметра:
- Общую массу кровельной конструкции;
- Пиковые уровни снежных осадков, свойственные региону, где проходит строительство.
Упрощенный алгоритм расчетов сводится к следующим действиям:
- Сначала нужно определить вес одного квадратного метра кровельного пирога;
- Полученное значение умножается на общую площадь кровли;
- Масса кровли умножается на коэффициент 1,1.
Пример расчета уклона кровли в градусах
Чтобы понять, как высчитать угол крыши, стоит рассмотреть процесс расчетов на конкретном примере. Для примера будут взяты следующие данные: обрешетка имеет толщину 2,5 см, один квадратный метр кровли весит 15 кг, в качестве теплоизоляционного материала используется утеплитель толщиной 10 см, квадратный метр которого имеет вес 10 кг, а для покрытия используется ондулин с весом 3 кг на квадратный метр.
Расчет ската крыши проводится в соответствии с описанной выше методикой. Подстановка имеющихся данных приводит к следующему выражению: (15+10+3)х1,1 = 30,8 кг/кв.м. Полученная величина вполне допустима – среднестатистическая нагрузка на крышу жилых зданий составляет немногим меньше 50 кг/кв.м. Кроме того, в формуле присутствует коэффициент 1,1, который немного увеличивает фактический вес кровельной конструкции и позволяет в дальнейшем заменить кровельное покрытие на более тяжелое.
Как узнать угол наклона крыши
Между уклоном кровельных скатов и снежной нагрузкой имеется прямая зависимость. Если угол наклона крыши меньше 25 градусов, то коэффициент снежной нагрузки равен 1, а при углах, варьирующихся в пределах от 25 до 60 градусов, то этот коэффициент увеличивается до 1,25. Крыша с большим углом наклона не будет подвергаться снежным нагрузкам вообще, поэтому они не учитываются при расчетах.
Чтобы определить угол наклона крыши, нужно воспользоваться таблицей Брадиса и простой методикой: высота кровельной конструкции делится на длину фронтона, разделенную на два, после чего остается найти таблице угол, который соответствует полученному результату.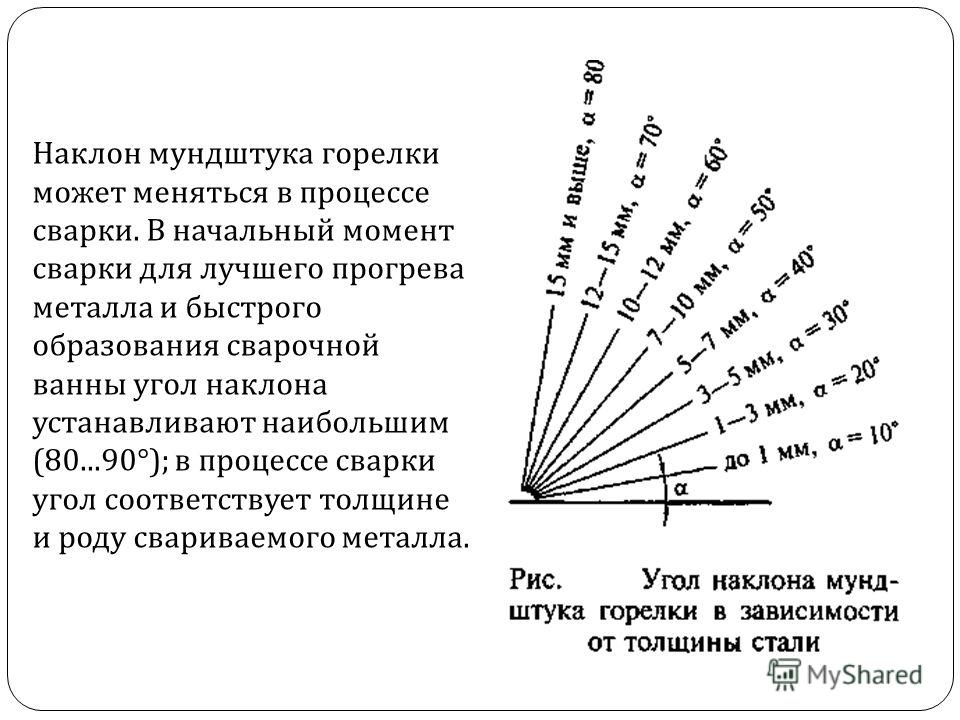
Высота крыши в коньке определяется следующим образом:
- Первым делом нужно рассчитать ширину пролета;
- Полученная величина делится на 2;
- Чтобы сделать расчет высоты конька, результат предыдущего расчета умножается на коэффициент, соответствующий определенному углу наклона.
На примере реализация такой методики расчета выглядит так: при ширине здания, равной 8 метрам, и 25-градусном уклоне кровли, расчетный коэффициент составляет 0,47. В итоге подстановки значений получается выражение следующего вида: 4х0,47 = 1,88 м. Полученная величина – это высота крыши, соответствующая имеющимся исходным данным.
Выбор кровельного покрытия в зависимости от наклона крыши
На рынке материалы для крыши присутствуют в большом ассортименте, поэтому с выбором подходящего варианта особых проблем не будет. Кровельные покрытия отличаются по характеристикам и возможностям применения, и все их параметры необходимо изучить перед тем, как измерить угол крыши – только в этом случае удастся создать надежную и эффективную конструкцию.
Выбирая материал для кровли, стоит отталкиваться от следующих рекомендаций:
- Если угол наклона стропил составляет от 2,5 до 10 градусов, то лучше всего подойдут покрытия из каменной крошки или гравия. В первом случае верхний слой покрытия имеет толщину 3-5 мм, а во втором – 10-15 мм.
- При наклоне более 10 градусов оптимальным вариантом будут крупнозернистые или рулонные материалы, дополненные битумной гидроизоляцией.
- Для обустройства скатных крыш с углом наклона не более 20 градусов обычно используется профнастил или листовой асбестоцемент. Все швы и стыки между кровельными материалами должны быть обработаны герметиком.
- Если угол наклона крыши находится в пределах 20-60 градусов, то она чаще всего накрывается металлическими листами. Стыки материалов в данном случае нужно в обязательном порядке герметизировать.
Заключение
Знание того, как узнать угол наклона крыши в градусах, существенно упростит процесс ее проектирования и позволит создать максимально надежную конструкцию, которая сможет хорошо защищать коробку здания от атмосферных осадков, ветра и холода.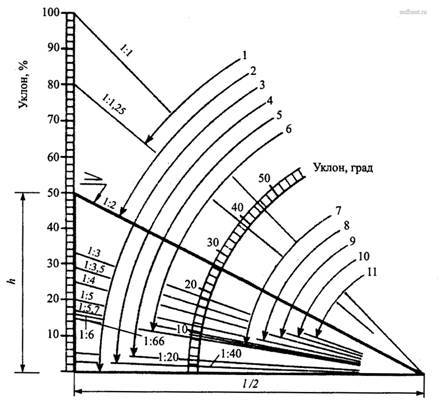
Расчет уклона и общего уклона в архитектуре
Архитекторы постоянно предоставляют информацию об уклоне на своих чертежах, используя градиенты, градусы или проценты в зависимости от приложения. Например, крыши обозначаются градиентами, а поперечные уклоны тротуаров обычно указываются в градусах. Полезно понять, как рассчитать каждый метод.
Есть три различных способа указать наклон поверхности относительно горизонтальной плоскости: градусы, уклон и процент.
Расчет градиента уклона
Градиенты уклона записываются как Y: X, где Y — это единичная величина подъема, а X — это пробег. Оба числа должны использовать одни и те же единицы измерения. Например, если вы путешествуете на 3 дюйма по вертикали и 3 фута (36 дюймов) по горизонтали, наклон будет 3:36 или 1:12. Это читается как «наклон один из двенадцати».
Оба числа должны использовать одни и те же единицы измерения. Например, если вы путешествуете на 3 дюйма по вертикали и 3 фута (36 дюймов) по горизонтали, наклон будет 3:36 или 1:12. Это читается как «наклон один из двенадцати».
Расчет процента уклона
Процент уклона рассчитывается так же, как и уклон.Преобразуйте приближение и бег в те же единицы, а затем разделите приближение на разбег. Умножьте это число на 100, и вы получите наклон в процентах. Например, подъем 3 дюйма, разделенный на 36 дюймов = 0,083 x 100 = уклон 8,3%.
Расчет уклона в градусах
Самый сложный способ вычисления наклона — в градусах, и для этого требуется немного математики средней школы. Тангенс данного угла (в градусах) равен подъему, деленному на пробег. Следовательно, величина, обратная тангенсу подъема, деленная на длину пробега, даст угол.
Таблица общих наклонов в архитектуре
В таблице ниже показаны некоторые распространенные уклоны. Для полов с уклоном 1:20 поручни не требуются, но все, что круче 1:20, считается пандусом и требует поручней. Пандусы с уклоном 1:12 — это максимальный уклон, разрешенный правилами ADA, и для них требуются поручни. Федеральные коды ADA указывают, что максимальный поперечный уклон доступного маршрута составляет 1:48, что чуть больше 2%. Однако мы видели некоторые юрисдикции, которые допускают максимальный поперечный уклон 1:50.
Пандусы с уклоном 1:12 — это максимальный уклон, разрешенный правилами ADA, и для них требуются поручни. Федеральные коды ADA указывают, что максимальный поперечный уклон доступного маршрута составляет 1:48, что чуть больше 2%. Однако мы видели некоторые юрисдикции, которые допускают максимальный поперечный уклон 1:50.
| Градусов | Градиент | Процент |
|---|---|---|
| 0,6 ° | 1: 95,49 | 1,0% |
| 1 ° | 1: 57.29 | 1,7% |
| 1,15 ° | 1 : 50 | 2% |
| 1,19 ° | 1: 48 | 2,08% |
| 2,86 ° | 1: 20 | 5% |
| 4,76 ° | 1: 12 | 8 .3% |
| 7,13 ° | 1: 8 | 12,5% |
| 10 ° | 1: 5,67 | 17,6% |
| 14,04 ° | 1: 4 | 25% |
| 15 ° | 1: 3,73 | 26,8% |
| 26,57 ° | 1: 2 | 50% |
| 30 ° | 1: 1,73 | 57,7% |
| 45 ° | 1: 1 | 100% |
56. 31 ° 31 ° | 1: 0,67 | 150% |
| 60 ° | 1: 0,6 | 173,2% |
| 63,43 ° | 1: 0,5 | 200% |
| 78,69 ° | 1 : 0,2 | 500% |
| 89,43 ° | 1: 0,1 | 1000% |
| 90 ° | 1: 0 | инф. |
Скаты крыши
Наклоны крыши идентифицируются с помощью описанного выше градиентного метода, где подъем меняется, но обычно длина спуска составляет 12.На некоторых очень крутых крышах вы можете увидеть инвертированный градиент, так что длина пролета меняется, но подъем сохраняется как 12.
Кровля с малым уклоном
Кровли с низким уклоном имеют уклон 3:12 или меньше. У них должна быть мембранная кровельная система для обеспечения водонепроницаемости.
| Градиент крыши | Градусов | Процент |
|---|---|---|
| 1/4: 12 | 1,19 ° | 2,08% |
| 1/2: 12 | 2,39 ° | 4. 17% 17% |
| 1: 12 | 4,76 ° | 8,3% |
| 2: 12 | 9,46 ° | 16,67% |
| 3: 12 | 14,04 ° | 25% |
Крутые крыши
Все, что выше 3:12, считается крутой крышей и может быть покрыто металлическими панелями, черепицей или черепицей — эти крыши проливают воду и не считаются водонепроницаемыми.
| Градиент крыши | Градусов | Процент |
|---|---|---|
| 4: 12 | 18.43 ° | 33,33% |
| 5: 12 | 22,62 ° | 41,67% |
| 6: 12 | 26,57 ° | 50% |
| 7: 12 | 30,26 ° | 58,33 % |
| 8: 12 | 33,69 ° | 66,67% |
| 9: 12 | 36,87 ° | 75% |
| 10: 12 | 39,81 ° | 83,33% |
| 11: 12 | 42.51 ° | 91,67% |
| 12: 12 | 45 ° | 100% |

Измерение уклона и уклона крыши
Ник Громицко, CMI® и Бенджамин ГромицкоИ наклон, и наклон указывают на наклон крыши, выраженный как пропорция вертикали к горизонтали. В этой статье описывается как наклон крыши, так и уклон крыши, а также различия между ними, поскольку они не совпадают. Поскольку уклон влияет на способ установки кровельных систем, в том числе определяет, какой тип кровельного материала может быть применен, понимание того, как измерить уклон крыши, может быть полезным для домашнего инспектора.
На приведенном выше рисунке показана простая двускатная крыша и общая взаимосвязь между подъемом, пролетом и пролетом. Каркас крыши — это практическое применение геометрии, а уклон крыши во многом основан на свойствах прямоугольного треугольника.
В конструкции крыши основание прямоугольного треугольника называется пролетом. Маршрут — это расстояние от внешней стороны верхней плиты стены до точки, находящейся непосредственно под центром конька.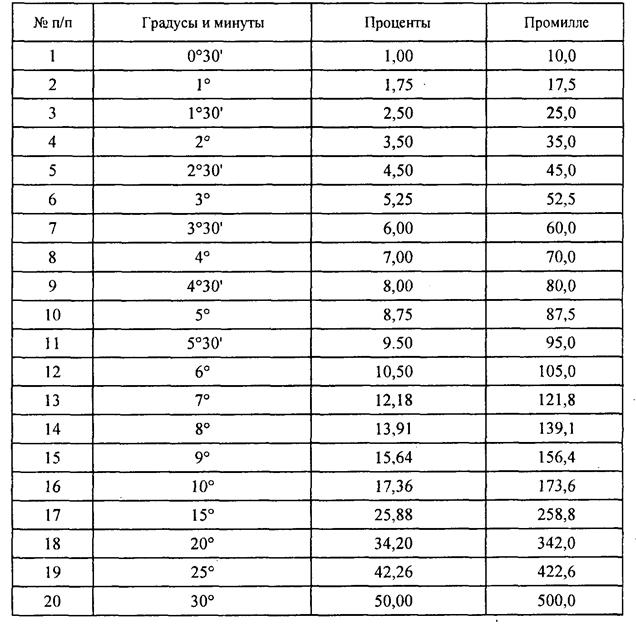 Вертикальная сторона треугольника называется подъемом, т.е. расстоянием, на которое стропильная доска крыши выступает вверх над верхней пластиной стены.
Вертикальная сторона треугольника называется подъемом, т.е. расстоянием, на которое стропильная доска крыши выступает вверх над верхней пластиной стены.Уклон
Уклон — это уклон крыши, выраженный как отношение вертикального подъема к горизонтальному пролету, где пролет представляет собой некоторую часть пролета. Это соотношение всегда выражается в дюймах на фут.
Коэффициент уклона
Говорят, что крыша, которая поднимается на 4 дюйма на каждые 1 фут или 12 дюймов пробега, имеет уклон «4 на 12». Если подъем составляет 6 дюймов на каждые 12 дюймов пробега, то уклон крыши составляет «6 к 12».Наклон можно численно выразить как отношение.Коэффициент уклона представляет собой определенный подъем по вертикали на каждые 12 дюймов горизонтального пробега. Например, наклон «4 из 12» можно выразить как соотношение 4:12. Наклон «6 из 12» выражается как 6:12.
Треугольный символ над линией крыши на этом архитектурном фасаде предоставляет информацию о , ro или уклоне.
- в виде отношения; и
- дюймов на фут.
Шаг
Pitch Fraction
Исторически слово «шаг» означало отношение высоты конька к полному пролету / ширине здания или отношение длины стропил к ширине здания. А тогда гребень обычно находился в середине пролета.В современной строительной практике этого больше нет. Гребень может быть размещен в любом месте пролета, непосредственно от середины до любой конечной точки пролета.
Говорят, что крыша, которая поднимается на 8 футов на 24-футовый пролет, имеет уклон «от 1 до 3». Если подъем составляет 4 фута на 24-футовом пролете, то уклон крыши считается «от 1 до 6».
Шаг можно численно выразить дробью. Доля шага представляет собой определенную величину вертикального подъема по всему пролету. Например, для крыши с подъемом в 4 фута и пролетом в 24 фута шаг составляет от 1 до 6, что может быть выражено как часть 1/6.Шаг «от 12 до 24» выражается как 1/2.
Например, для крыши с подъемом в 4 фута и пролетом в 24 фута шаг составляет от 1 до 6, что может быть выражено как часть 1/6.Шаг «от 12 до 24» выражается как 1/2.
Термины «шаг» и «наклон» часто используются как синонимы, что неверно. Они не означают одно и то же. Наклон дает более ценную информацию, чем шаг, как определено в этой статье.
Используя иллюстрацию выше и информацию, которую мы только что узнали о наклоне и шаге, мы можем видеть, что уклон 2:12 можно выразить как шаг 1/12, предполагая, что пролет в два раза больше длины пробега. Если уклон 4:12, шаг для 24-футового пролета будет 1/6.Если шаг 1/3, наклон 8:12. Помните, что наклон выражается в дюймах на фут. А шаг — это дробная часть, полученная путем деления повышения на весь диапазон.Минимальный уклон для различных кровельных покрытий
Международный жилищный кодекс (IRC) определяет минимальные требования к кровельным покрытиям и обязывает использовать инструкции производителя кровельного покрытия по установке.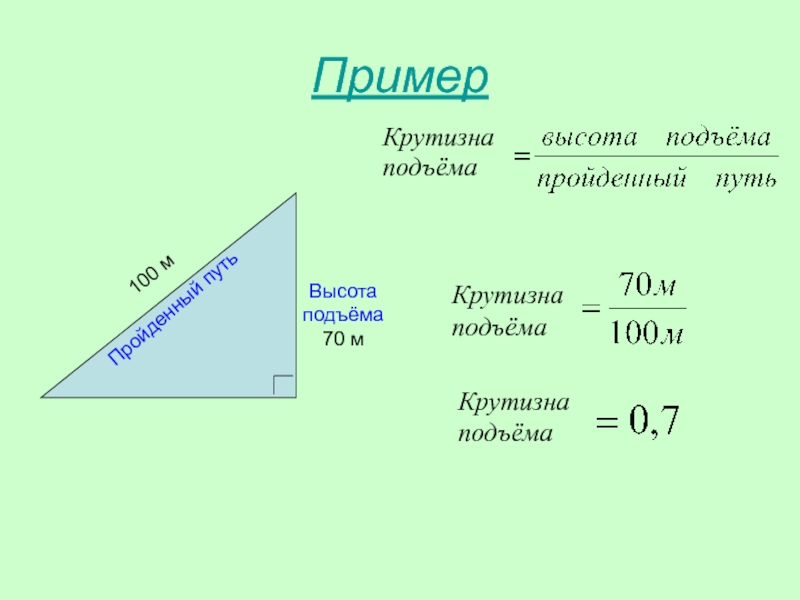
- Асфальтовую черепицу следует укладывать на крышах с уклоном 2:12 или больше (2015 IRC R905.2.2).
- Глиняную и бетонную черепицу следует укладывать на скаты крыши 2,5: 12 или больше (2015 IRC R905.3.2).
- Металлическая черепица должна быть установлена на кровлях с уклоном 3:12 или больше (2015 IRC R905.4.2).
- Рулонная кровля с минеральным покрытием должна быть установлена на скатах кровли 1:12 или больше (2015 IRC R905.4.2).
- Сланцевую черепицу следует укладывать на крышах с уклоном 4:12 или больше (2015 IRC R905.6.2).
- Деревянная черепица должна быть установлена на кровлях с уклоном 3:12 или больше (2015 IRC R905.7.2).
- Деревянные вибраторы следует устанавливать на крышах с уклоном 3:12 или выше (2015 IRC R905.8.2).
- Застроенные крыши должны устанавливаться на уклонах кровли 0,25: 12 или больше (2015 IRC R905.9.1), за исключением кровель из каменноугольной смолы, у которых минимальный уклон крыши составляет 1/8 единицы по вертикали на 12 единиц по горизонтали.
 (Уклон 1%).
(Уклон 1%). - Металлические кровельные панели должны устанавливаться на скатах крыши в соответствии с определенными швами (2015 IRC R905.10.2):
- минимальный уклон крыши 3:12 для металлических крыш внахлест, непаянных швов без нанесенного герметика
- минимальная крыша наклон 0.5:12 для металлических кровель внахлест, непаянных фальцев с нанесенным герметиком
- минимальный уклон крыши 0,25: 12 для фальцевых кровельных систем
- Модифицированная битумная кровля должна быть установлена на скатах кровли 0,25: 12 или больше (2015 IRC R905.11.1).
- Термореактивная однослойная кровля должна устанавливаться на скатах кровли 0,25: 12 или больше (2015 IRC R905.12.1).
- Однозонная кровля из термопласта должна устанавливаться на скатах кровли 0,25: 12 или больше (2015 IRC R905.13.1).
- Кровельное покрытие из напыляемой пенополиуретана должно быть установлено на скатах крыши 0,25: 12 или больше (2015 IRC R905.
 14.1).
14.1). - Жидкая кровля должна быть установлена на скатах кровли 0,25: 12 или больше (2015 IRC R905.15.1).
- Фотовольтаическая черепица должна быть установлена на скатах крыши 2:12 или больше (2015 IRC R905.16.2).
Битумная черепица
Наклон крыши влияет на поверхностный отвод воды и может определять тип кровельных материалов, которые должны быть установлены.Асфальтовую черепицу следует использовать только на кровлях с уклоном 2:12 и более. Крыши из асфальта и гальки предназначены для отвода воды, а не для использования в качестве водонепроницаемого барьера. Наклон крыши влияет на ее способность отводить воду и определяет пределы использования битумной черепицы.
Большинство битумной черепицы можно использовать на скатах крыш с 4:12 до 21:12, используя стандартные методы нанесения. Асфальтовую черепицу можно использовать на склонах с 2:12 до 3,9:12, если соблюдаются специальные процедуры укладки на пологих склонах.Инспектор обычно находит рулонные кровельные материалы, установленные на уклонах менее 4:12.
Измерение уклона
Вам понадобится плотницкий уровень, рулетка и карандаш.
Отмерьте 12 дюймов от одного конца уровня и сделайте отметку.
Измерения можно снимать на недостроенном чердаке под крышей, на граблях или поверх кровельных материалов. Измерение уклона от поверхности крыши может не дать наиболее точного измерения из-за неровной поверхности кровельного покрытия.
Заползти в недостроенный чердак. Найдите легкодоступную кровельную доску. Приложите конец уровня к нижнему краю стропила крыши и держите ровно. Измерьте расстояние от 12-дюймовой отметки на уровне по вертикали до нижнего края стропила. Это количество дюймов, на которое крыша поднимается на 12 дюймов.
Найдите легкодоступную доску для граблей. Держите плотника ровно ровно, прижимая конец к нижнему краю грабельной доски.Измерьте расстояние от 12-дюймовой отметки на уровне по вертикали до того места, где рулетка касается нижнего края грабельной доски. Это количество дюймов, на которое крыша поднимается на 12 дюймов.
Измерение уклона крыши от поверхности крыши будет неточным без использования чего-либо, чтобы сделать плоскую поверхность для измерения уклона. Использование 48-дюймового плотницкого уровня или прямой доски 2х4 может оказаться полезным для создания гладкой поверхности, отражающей наклон крыши.
Инспектор может счесть полезным использование мобильных технологий. Существуют приложения для мобильных устройств, которые точно измеряют уклон крыши, в том числе возможность делать цифровые снимки уклона с земли.
Резюме
Шаг и наклон не означают одно и то же. Уклон — это отношение, измеряемое в дюймах на фут. Поскольку уклон влияет на отвод воды с поверхности крыши и определяет пределы использования асфальтовой черепицы, понимание того, как измерить уклон крыши, может быть полезным для домашнего инспектора.
.
Как измерить угол наклона крыши | Home Guides
Наклон крыши влияет на стоимость строительства, а также на внешнюю привлекательность дома.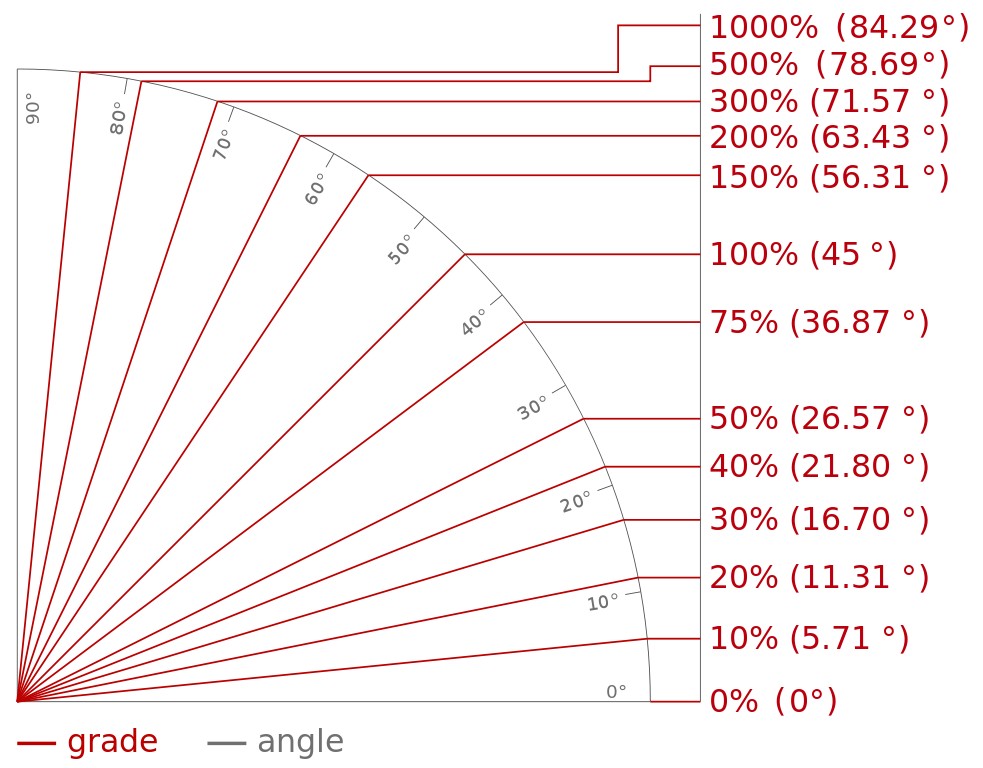 Определение уклона или наклона крыши — это простое математическое упражнение, которое можно выполнить на крыше, на чердаке или на потолке. Поскольку эти три метода одинаково эффективны, выберите метод чердака или метод потолка из-за меньшего риска, что вам не придется забираться на крышу.
Определение уклона или наклона крыши — это простое математическое упражнение, которое можно выполнить на крыше, на чердаке или на потолке. Поскольку эти три метода одинаково эффективны, выберите метод чердака или метод потолка из-за меньшего риска, что вам не придется забираться на крышу.
Интерьер
Заберитесь на чердак.Найдите стропило на крыше. Стропила — это длинные наклонные балки, идущие от стен до пика крыши.
Отмерьте 12 дюймов от конца уровня и сделайте отметку. Вы будете использовать эту 12-дюймовую секцию для определения уклона.
Найдите наиболее доступную для вас часть стропила. Поскольку стропила прямые, их уклон не меняется по длине стропила, поэтому не имеет значения, какое сечение стропил вы выберете для измерения. Держите плотник ровно горизонтально, прижимая его конец к стороне стропила, обращенной к полу.Убедитесь, что край, касающийся стропила, — это тот край, от которого вы отмерили и отметили 12 дюймов.
Измерьте расстояние от верха уровня на отметке 12 дюймов до того места, где рулетка снова коснется стропила. Горизонтальный уровень, вертикальная лента и диагональное стропило образуют треугольник. Например, если уровень находится в шести дюймах от низа стропил на отметке 12 дюймов, уклон крыши будет 6 дюймов-12. Это означает, что более 12 дюймов по горизонтали наклон повышается на 6 дюймов. Каждый дюйм равен 3.75 градусов, поэтому угол наклона 6 дюймов 12 составляет 22,5 градуса.
Горизонтальный уровень, вертикальная лента и диагональное стропило образуют треугольник. Например, если уровень находится в шести дюймах от низа стропил на отметке 12 дюймов, уклон крыши будет 6 дюймов-12. Это означает, что более 12 дюймов по горизонтали наклон повышается на 6 дюймов. Каждый дюйм равен 3.75 градусов, поэтому угол наклона 6 дюймов 12 составляет 22,5 градуса.
Внешний вид
Отмерьте 12 дюймов от конца уровня и сделайте отметку. Вы будете использовать эту часть уровня для измерения уклона. Поставьте лестницу на устойчивое место у дома и поднимитесь на потолок.
Держите плотника ровно в горизонтальном положении, прижимая конец к низу потолка. Софит — это область под крышей, которая простирается над внешней стеной дома.
Измерьте расстояние от вершины уровня на отметке 12 дюймов до того места, где рулетка снова коснется потолка. Например, если уровень находится в четырех дюймах от потолка и отметке 12 дюймов, уклон крыши составляет 4 дюйма из 12. Это означает, что при высоте более 12 дюймов наклон увеличивается на 4 дюйма. Каждый дюйм равен 3,75 градуса, поэтому угол наклона 4 в 12 составляет 15 градусов.
Это означает, что при высоте более 12 дюймов наклон увеличивается на 4 дюйма. Каждый дюйм равен 3,75 градуса, поэтому угол наклона 4 в 12 составляет 15 градусов.
Веб-страница не найдена на InspectApedia.com
.
Что делать, если ссылка на веб-страницу на InspectApedia.com приводит к ошибке страницы 404
Это так же просто, как … ну,
выбирая из 1, 2 или 3- Воспользуйтесь окном поиска InspectAPedia в правом верхнем углу нашей веб-страницы, найдите нужный текст или информацию, а затем просмотрите ссылки, которые возвращает наша пользовательская поисковая система Google
- Отправьте нам электронное письмо напрямую с просьбой помочь в поиске информации, которую вы искали — просто воспользуйтесь ссылкой СВЯЗАТЬСЯ С НАМИ на любой из наших веб-страниц, включая эту, и мы ответим как можно скорее.
- Используйте кнопку НАЗАД вашего веб-браузера или стрелку (обычно в верхнем левом углу экрана браузера рядом с окном, показывающим URL-адрес страницы, на которой вы находитесь), чтобы вернуться к предыдущей статье, которую вы просматривали.
 Если вы хотите, вы также можете отправить нам электронное письмо с этим именем или URL-адресом веб-страницы и сообщить нам, что не сработало и какая информация вам нужна.
Если вы хотите, вы также можете отправить нам электронное письмо с этим именем или URL-адресом веб-страницы и сообщить нам, что не сработало и какая информация вам нужна.Если вы действительно хотите нам помочь, используйте кнопку НАЗАД в своем браузере, затем скопируйте URL-адрес веб-страницы, которую вы пытались загрузить, и воспользуйтесь нашей ссылкой СВЯЗАТЬСЯ С НАМИ (находится как вверху, так и внизу страницы), чтобы отправьте нам эту информацию по электронной почте, чтобы мы могли решить проблему.- Спасибо.
Приносим свои извинения за этот SNAFU и обещаем сделать все возможное, чтобы быстро ответить вам и исправить ошибку.
— Редактор, InspectApedia.com
Задайте вопрос или введите условия поиска в поле поиска InspectApedia чуть ниже.
Мы также предоставляем МАСТЕР-ИНДЕКС по этой теме, или вы можете попробовать верхнюю или нижнюю панель ПОИСКА как быстрый способ найти необходимую информацию.
Зеленые ссылки показывают, где вы находитесь. © Copyright 2017 InspectApedia.com, Все права защищены.
Издатель InspectApedia.com — Дэниел Фридман .Расчет параметров скатной кровли на примере вальмовой
Чтобы рассчитать кровельные материалы, необходим документ, который по ГОСТ 21.501-93 «Правила выполнения архитектурно-строительных чертежей» называется план кровли (крыши). Для корректного расчёта параметров достаточно вида крыши сверху с обозначенными направлениями скатов, длин проекций и высотными отметками.
На рисунке представлен общий вид дома с конструкцией вальмовой крыши. Данный тип крыши состоит из 4-х скатов (плоскостей): два треугольных ската (вальмы) и две трапеции.
Для точного определения размеров кровли необходимо знать уклоны скатов кровли (крыши). Уклон ската – угол наклона ската по отношению к горизонту. Может выражаться в градусах, в процентах, дробях.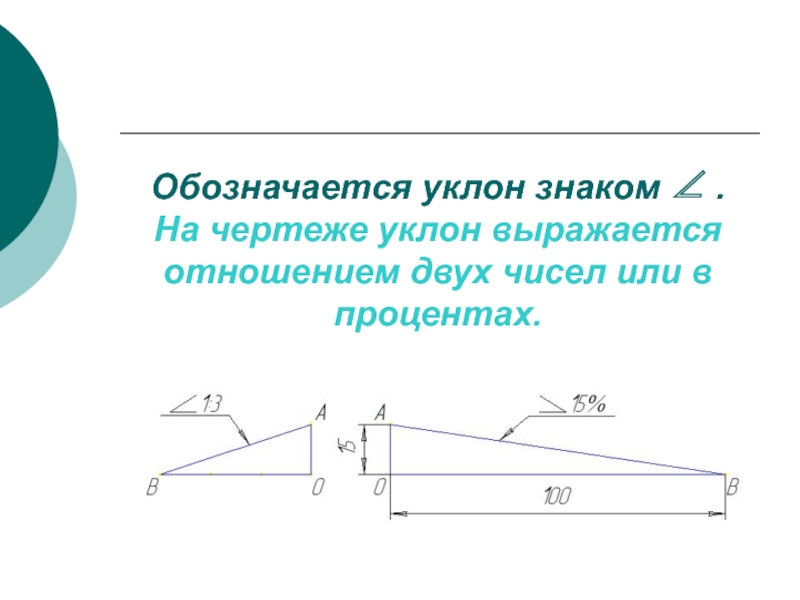
Если на плане кровли не указаны уклоны, измерить их можно с помощью транспортира по планам фасадов. С большей степенью точности можно вычислить, зная проекционные и высотные размеры кровли. Так как отношение этих двух величин постоянное для конкретного уклона, градусность будет определена предельно точно.
Интересные факты, известные из курса школьной геометрии:
- Если проекция ската равна изменению его высоты, уклон кровли будет равным 45 градусов;
- Длина ската, уклон которого равен 30-ти градусам в два раза больше его высоты. А длина ската с уклоном 60 градусов в два раза больше её проекции.
Для первого примера отношение высоты к проекции 1:1, а длина ската будет больше её проекции в 1,414 раза. Таким образом, 1,414 — коэффициент уклона ската с уклоном 45 градусов. Для уклона 60 градусов этот коэффициент равен 2,000, а для 30 – 1,155.
Следовательно, параметры ската в рамках конкретной кровли взаимосвязаны, и могут быть вычислены при известности двух из них.
Следующая задача, которую предстоит решать специалисту в ходе расчёта кровельных материалов, заключается в определении площади кровли, а так же суммарных длин всех её одноименных элементов: коньков, хребтов, карнизов. Для других конфигурация кровли могут быть ещё: ендовы, примыкания, фронтоны (щипцы, торцы) и так далее.
При определении площади следует разбить её на составляющие прямоугольники, треугольники, трапеции, при необходимости, круги и другие фигуры.
Относительно рассматриваемой крыши, план кровли разделён естественным образом на два треугольника и две трапеции.
На следующем рисунке планы кровли и двух основных фасада:
Приступим к расчету геометрических параметров крыши:
L карниза = (10 + 6 )*2 = 32 м
L конька = 4 м
Определим длины скатов. Они равны между собой исходя из плана кровли.
Смотрим на план кровли и видим, что длина ската по плану кровли составляет 3м. Однако это все же не искомая длина ската, а всего лишь проекция этой длины на горизонтальную плоскость.
Чтобы преобразовать проекцию длины в действительный размер достаточно умножить проекцию на коэффициент 1,155 (для 30 градусов):
L ската = 3м * 1,155 = 3,465 м.
Также, длину ската можно найти по теореме Пифагора, если известна высота крыши (H = 1,732 м):
(L ската) ² = H ² + (проекция длины ската) ² = (1,732) ² + (3) ² = 2,999824 + 9 =11,999824
L ската =3,465 м.
Найденная длина ската(скатов) является определяющей высотой фигур (трапеции и треугольника) при расчете площадей:
S кровли = Sската 1 + Sската 2 + Sската 3 + Sската 4
S ската 1 = Sската 3 и S ската 2 = Sската 4
По формуле площади треугольника:
S ската 1= (6*3,465)/2 = 10,395 м²
По формуле площади трапеции:
S ската 2 = ((10+4)/2)*3,465 = 24,255 м²
Итого общая площадь кровли:
S кровли = 10,395 + 10,395 + 24,255 + 24,255 = 67,3 м²
Есть самый быстрый способ определения нашей искомой площади, заключается он в умножении площади проекции крыши (габариты крыши по плану кровли, 6м х 10м) на коэффициент 1,155 (по аналогии с определением длины ската):
S кровли = 6*10*1,155 = 69,3 м²
Оставшийся параметр – длину ребра(хребта) можно также определить по теореме Пифагора:
( L ребра(хребта) ) ² = 3 2 + (длины ската) ² = ( 3 ) ² + (3,465) ² = 9 + 12,006225 = 21,006225
L ребра(хребта) = 4,583 м
Существует также коэффициент пересчета для определения искомых длин ребер, для этого достаточно умножить длину ребра(хребта) по плану кровли на коэффициент пересчета (30град. /30град.), равным значению 1,08.
/30град.), равным значению 1,08.
Итак:
(L проекции хребра(хребта)) ² = 3 2 +3 2 = 18
Lпроекции хребра(хребта) = 4,24264068711
L ребра(хребта) = 4,24264068711 *1,08 = 4,583 м
Сумма длин всех ребер(хребтов): L ребер(хребтов) = 4,583*4 = 18,332 м
После того как все геометрические параметры крыши определены, мы сможем подобрать и рассчитать любой кровельный материал по нашему выбору.
Вариант расчета кровли BRAAS, модель «Франкфуртская»:
(Минимальный рекомендуемый угол крыши для данной модели составляет 16 градусов, удовлетворяет нашим требованиям).
Внешние габариты одной черепицы «Франкфуртская» составляют 330х420мм.
Поскольку черепица укладывается с нахлестом и с учетом стыковки черепицы между собой через замковое соединение полезная площадь покрытия одной черепицы будет несколько меньше и составит 300х330мм.
Полезная площадь покрытия для всех видов черепиц всегда разная и обусловена широким разнообразием профилей и их размеров.
При размерах 300х330мм расход на 1м² составляет:
1м²/(0,3м * 0,33м) = 10,1шт./м²
Общее количество рядовой черепицы на покрытие всей крыши:
10,1*69,3 м² = 700 шт.
Принимая во внимание возможный бой черепицы при доставке/разгрузке/монтаже, а также некоторые отклонения в фактических размерах от данных в проекте, обязательно учитывается технологический запас материала. Величина запаса зависит от геометрической сложности кровли и должна приниматься индивидуально для каждого крыши. Для вальмовой крыши будет достаточно 5%. Запас очень важен при расчете кровельного покрытия, т.к. предостерегает нас от нехватки материала при монтаже кровли.
В итоге, с учетом запаса нам необходимо:
700 шт. + 5% = 735шт.
Количество начальной хребтовой черепицы:
4 шт.
Количество рядовой коньковой черепицы (расход 2,5шт./мп):
2,5*18,332 = 46 шт.
46 шт. — 4 шт. (начальные хребтовые) = 42 шт.
Вальмовая черепица: 2 шт. (устанавливается на место пересечения конька и двух ребер)
А теперь, предлагаем посмотреть как выглядит подробный расчет кровельного покрытия в нашей компании с учетом крепежа и всех необходимых аксессуаров:
А также раздел 2 с крепежом и необходимыми аксессуарами:
В данной статье мы разобрали с вами расчет скатной типовой крыши имея при себе лист бумаги, карандаш и немножко знаний из школьной программы геометрии. Сложные кровли с большим количеством скатов разных геометрических форм, сложных многоугольников, а также криволинейных поверхностей (конусов, сфер и т.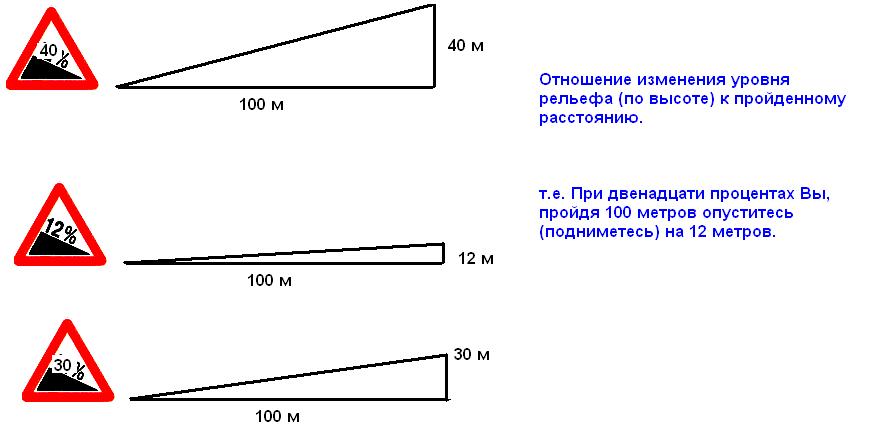 д.) рассчитываются программно на ПК в специальных инженерных пакетах. Это в значительной мере облегчает процесс расчета, экономит время и предостерегает нас от возможных арифметических ошибок при расчете.
д.) рассчитываются программно на ПК в специальных инженерных пакетах. Это в значительной мере облегчает процесс расчета, экономит время и предостерегает нас от возможных арифметических ошибок при расчете.
Угол 1 16 сколько градусов. Уклоны и конусность
Во многих деталях машин используются уклоны и конусность. Уклоны встречаются в профилях прокатной стали, в крановых рельсах, в косых шайбах и т. д. Конусности встречаются в центрах бабок токарных и других станков, на концах валов и ряда других деталей.
Уклон характеризует отклонение прямой линии от горизонтального или вертикального направлений. Для того чтобы построить уклон 1:1, на сторонах прямого угла откладывают произвольные, но равные величины (рис. 1). Очевидно, что уклон 1:1 соответствует углу в 45 градусов. Чтобы построить линию с уклоном 1:2, по горизонтали откладывают две единицы, для уклона 1:3 — три единицы и т. д. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а. Величину уклона на чертеже в соответствии с ГОСТ 2.307-68 указывают с помощью линии-выноски, на полке которой наносят знак уклона и его величину. Расположение знака уклона должно соответствовать определяемой линии: одна из прямых знака должна быть горизонтальна, другая — наклонена примерно под углом 30° в ту же сторону, как и сама линия уклона.
е. он выражается тангенсом угла а. Величину уклона на чертеже в соответствии с ГОСТ 2.307-68 указывают с помощью линии-выноски, на полке которой наносят знак уклона и его величину. Расположение знака уклона должно соответствовать определяемой линии: одна из прямых знака должна быть горизонтальна, другая — наклонена примерно под углом 30° в ту же сторону, как и сама линия уклона.
На рисунке в качестве примера построен профиль несимметричного двутавра, правая полка которого имеет уклон 1:16. Для ее построения находят точку А с помощью заданных размеров 26 и 10. В стороне строят линию с уклоном 1:16, для чего по вертикали откладывают, например, 5 мм, а по горизонтали 80 мм; проводят гипотенузу, направление которой определяет искомый уклон. С помощью рейсшины и угольника через точку А проводят линию уклона, параллельную гипотенузе.
Конусностью называют отношение диаметра основания к его высоте. В этом случае конусность К=d/l. Для усеченного конуса К = (d-d 1)/l . Пусть требуется построить конический конец вала по заданным размерам: d — диаметр вала — 25 мм; I — общая длина конца вала — 60 мм; l 1 — длина конической части — 42 мм; d 1 — наружный диаметр резьбы — 16 мм; К — конусность 1: 10 (рис. 3, б). Прежде всего, пользуясь осевой, строят цилиндрическую часть вала, имеющую диаметр 25 мм. Этот размер определяет также большее основание конической части. После этого строят конусность 1:10. Для этого строят конус с основанием, равным 10 мм, и высотой, равной 100 мм (можно было бы воспользоваться и размером 25 мм, но в этом случае высота конуса должна быть взята равной 250 мм, что не совсем удобно). Параллельно линиям найденной конусности проводят образующие конической части вала и ограничивают ее длину размером 42 мм. Как видно, размер меньшего основания конуса получается в результате построения. Этот размер обычно не наносят на чертеж. Запись М16X1,5 является условным обозначением метрической резьбы, о чем подробнее будет сказано дальше.
Пусть требуется построить конический конец вала по заданным размерам: d — диаметр вала — 25 мм; I — общая длина конца вала — 60 мм; l 1 — длина конической части — 42 мм; d 1 — наружный диаметр резьбы — 16 мм; К — конусность 1: 10 (рис. 3, б). Прежде всего, пользуясь осевой, строят цилиндрическую часть вала, имеющую диаметр 25 мм. Этот размер определяет также большее основание конической части. После этого строят конусность 1:10. Для этого строят конус с основанием, равным 10 мм, и высотой, равной 100 мм (можно было бы воспользоваться и размером 25 мм, но в этом случае высота конуса должна быть взята равной 250 мм, что не совсем удобно). Параллельно линиям найденной конусности проводят образующие конической части вала и ограничивают ее длину размером 42 мм. Как видно, размер меньшего основания конуса получается в результате построения. Этот размер обычно не наносят на чертеж. Запись М16X1,5 является условным обозначением метрической резьбы, о чем подробнее будет сказано дальше.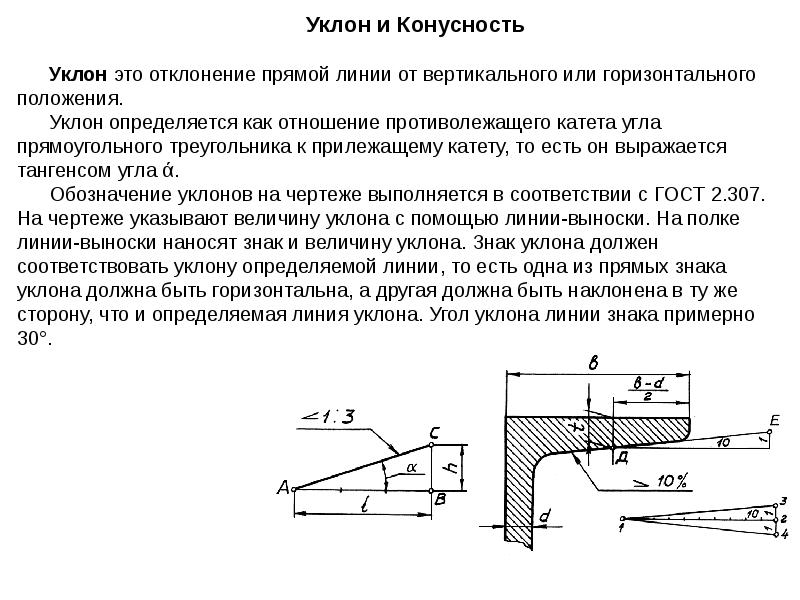
TBegin—>
TEnd—>
Рис. 1. Построение уклонов
Перед размерным числом, характеризующим конусность, наносят условный знак в виде равнобедренного треугольника, вершину которого направляют в сторону вершины самого конуса. Знак конусности располагают параллельно оси конуса над осью или на полке линии-выноски, заканчивающейся стрелкой, как в случае надписи уклона. Конусность выбирают в соответствии с ГОСТ 8593-57 .
Рис. 2. Пример построения уклонов
TBegin—>
TEnd—>
Рис. 3. Построение конусности
Основные нормы взаимозаменяемости
ХАРАКТЕРИСТИКИ ИЗДЕЛИЙ ГЕОМЕТРИЧЕСКИЕ
Нормальные конусности и углы конусов
ISO 1119:1998
Geometrical product specifications (GPS)
—
Series of conical tapers and taper angles
(MOD)
Москва |
Цели и принципы
стандартизации в Российской Федерации установлены Федеральным законом от 27
декабря 2002 г. № 184-ФЗ
«О техническом
регулировании», а правила применения национальных стандартов Российской
Федерации — ГОСТ Р
1.0-2004
«Стандартизация в Российской Федерации. Основные положения»
№ 184-ФЗ
«О техническом
регулировании», а правила применения национальных стандартов Российской
Федерации — ГОСТ Р
1.0-2004
«Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский и конструкторский институт средств измерений в машиностроении» (ОАО «НИИизмерения») на основе собственного аутентичного перевода на русский язык стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 242 «Допуски и средства контроля»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 4 декабря 2009 г. № 557-ст
4 Настоящий
стандарт является модифицированным по отношению к международному стандарту ИСО
1119:1998 «Геометрические характеристики изделий. Ряды конусностей и углов конусов» (ISO
1119:1998 «Geometrical product specifications (GPS) — Series of conical tapers
and taper angles», MOD).
При этом в него не включено приложение А (справочное) «Связи в матричной системе GPS» применяемого международного стандарта, которое нецелесообразно применять в национальной стандартизации в связи с тем, что оно содержит сведения о матричной модели Системы стандартов ИСО «Геометрические характеристики изделий (GPS)» и месте применяемого международного стандарта в ней, не относящиеся к объекту стандартизации.
В настоящий стандарт относительно применяемого международного стандарта внесены следующие технические отклонения:
— «Библиография» приведена в соответствие с содержанием стандарта и требованиями ГОСТ Р 1.5-2004 .
Указанное приложение, не включенное в настоящий стандарт, приведено в дополнительном .
Наименование настоящего стандарта изменено относительно наименования применяемого международного стандарта для приведения в соответствие с требованиями ГОСТ Р 1.5-2004 (пункт 3.5)
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту
публикуется в ежегодно издаваемом информационном указателе «Национальные
стандарты», а текст изменений и поправок — в ежемесячно издаваемых
информационных указателях «Национальные стандарты». В случав пересмотра
(замены) или отмены настоящего стандарта соответствующее уведомление будет
опубликовано в ежемесячно издаваемом информационном указателе «Национальные
стандарты». Соответствующая информация, уведомление и тексты размещаются также
в информационной системе общего пользования — на официальном сайте Федерального
агентства по техническому регулированию и метрологии в сети Интернет
В случав пересмотра
(замены) или отмены настоящего стандарта соответствующее уведомление будет
опубликовано в ежемесячно издаваемом информационном указателе «Национальные
стандарты». Соответствующая информация, уведомление и тексты размещаются также
в информационной системе общего пользования — на официальном сайте Федерального
агентства по техническому регулированию и метрологии в сети Интернет
В настоящем стандарте использованы нормативные ссылки на следующие стандарты: ГОСТ Р 50017-92 (ИСО 575-78) Машины текстильные и оборудование вспомогательное. Патроны конические переходные. Половина угла конуса 4°20″. Размеры и методы контроля ГОСТ Р 50018-92 (ИСО 324-78) Машины текстильные и оборудование вспомогательное. Патроны конические для крестовой намотки при крашении (крестовая намотка). Половина угла конуса 4°20″. Размеры и методы контроля ГОСТ
Р 50042-92 (ИСО 368-82) Машины текстильные и оборудование вспомогательное. ГОСТ Р 50213-92 (ИСО 5237-78) Машины текстильные и оборудование вспомогательное. Патроны конические для намотки пряжи (крестовая намотка). Половина угла конуса 5°57. Размеры и методы контроля ГОСТ Р 50663-99 (ИСО 8382-88) Аппараты искусственной вентиляции легких для оживления. Общие технические требования и методы испытаний А.1 Информация о стандарте и его применении Настоящий международный стандарт содержит определение конусности и угла конуса, значения конусностей и углов конусов общего и специального назначения, а также области их применения. Для обеспечения однозначного понимания требований он должен быть дополнен стандартами, включающими связующие звенья с 3-го по 6-й. А.2 Положение в матричной системе GPS Настоящий международный
стандарт является общим стандартом GPS; его положения следует учитывать в связующих звеньях 1 и 2
серий стандартов на углы в общей матрице GPS, как показано на рисунке А. А.3 Связанные стандарты Связанные стандарты являются стандартами серий стандартов, указанных на рисунке А.1 Рисунок А.1 ИСО/ТР 14638:1995 Геометрические характеристики изделий (GPS). Основная схема. Приложение
ДБ Таблица ДБ.1
ИСО 8489-5:1995Машины
текстильные и вспомогательное оборудование. ИСО 8489-3:1995Машины текстильные и вспомогательное оборудование. Конусы крестовой намотки. Часть 3. Размеры, допуски и обозначения конусов с половиной угла при вершине 4°20″ ИСО 8489-4:1995Машины текстильные и вспомогательное оборудование. Конусы крестовой намотки. Часть 4. Размеры, допуски и обозначения конусов с половиной угла при вершине 4°20″, используемых для намотки при крашении ИСО 8489-2:1995Машины текстильные и вспомогательное оборудование. Конусы крестовой намотки. Часть 2. Размеры, допуски и обозначения конусов с половиной угла при вершине 3°30″ ИСО 239:1974Конусы сверлильные патронов ИСО 594-1:1986Наконечники конические с конусностью 6% (тип Люэра) для шприцев, игл и другого медицинского оборудования. Часть 1. Общие требования ИСО 595-1:1986Шприцы
медицинские цельностеклянные или металлостеклянные многократного применения.
Часть 1. ИСО 595-2:1987Шприцы медицинские цельностеклянные или металлостеклянные многократного применения. Часть 2. Конструкция Ключевые слова: угол конуса, конусность | ||||||||||||||||||||||||||||||||||||||
Основным нормативным документом для определения уклона пандуса и его длины в РФ является С Изменением №1 — актуализированная версия СНиП 35-01-2001.
Допустимые значения угла наклона пандуса
— Допустимый угол уклона пандуса должен быть не круче 1:20 (5%), а максимальная высота одного подъема (марша) пандуса не должна превышать 0,8 м.— При перепаде высот пола на путях движения 0,2 м и менее допускается увеличивать уклон пандуса до 1:10 (10%)
— На временных сооружениях или объектах временной инфраструктуры допускается максимальный уклон пандуса 1:12 (8%) при условии, что подъем по вертикали между площадками не превышает 0,5 м, а длина пандуса между площадками — не более 6,0 м.
— Пандусы при перепаде высот более 3,0 м и расчетной длиной более 36 м следует заменять лифтами, подъемными платформами и т.
 п
п— В соответствии с приказом Минстроя России №750/пр от 21 октября 2015 г. «Об утверждении изменений №1 к СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» «При проектировании реконструируемых, подлежащих капитальному ремонту и приспосабливаемых существующих зданий и сооружений уклон пандуса принимается в интервале от 1:20 (5%) до 1:12 (8%)».
Что обозначают цифры
1:10 — 10% — один к десяти, т.е. при перепаде высот в 1 м, длина пандуса должна быть 10 м, при высоте 0,5 м — длина пандуса должна быть 5 м и т.д.
В этом случае угол уклона пандуса будет соответствовать 5,7 градусам.
1:12 — 8% — один к двенадцати, т.е. при перепаде высоты в 1 м, длина пандуса должна быть 12 м, при высоте 0,5 м — длина пандуса должна быть не менее 6 метров и т.д.
Угол уклона пандуса будет равен 4,8 градусам.
1:20 — 5% — один к двадцати, т.е. при перепаде высот 1 м, длина пандуса должна быть 20 м, при высоте 0,5 м — 10 м.
Угол уклона пандуса будет равен 2,9 градусам.
Какой длины делать пандус?
Расчет длины пандуса в зависимости от высоты | |||
Высота пандуса, м | Длина пандуса, м | ||
(используется при перепаде высот менее 0,2 м) | (для временных, приспосабливаемых и реконструируемых сооружений) | (стандартный показатель) | |
Зеленый — допустимые значения, красный — недопустимые.

На изображениях конических элементов деталей размеры могут быть проставлены различно: диаметры большего и меньшего оснований усеченного конуса и его длина; угол наклона образующей (или угол конуса) или величина конусности и диаметр основания, длина и т.п.
Конусность
Отношение разности диаметров двух поперечных сечений конуса (D-d. ) к расстоянию между ними (l ) (рис. 6.39, а ) называется конусностью (К ): К = (D – d )/l.
Рис. 6.39.
Например, конический элемент детали с диаметром большего основания 25 мм, диаметром меньшего основания 15 мм, длиной 50 мм будет иметь конусность К = (D – d )/l = (25 – 15)/50 = 1/5 = 1:5.
При проектировании новых изделий применяются величины конусности, установленные ГОСТ 8593–81: 1:3; 1:5; 1:7; 1:8; 1:10; 1:12; 1:15; 1:20; 1:30. Стандартизированы также величины конусности, которые имеют элементы деталей с часто встречающимися углами между образующими конуса: углу 30° соответствует конусность 1:1,866; 45° – 1:1,207; 60° – 1:0,866; 75° – 1:0,652; углу 90° – 1:0,5.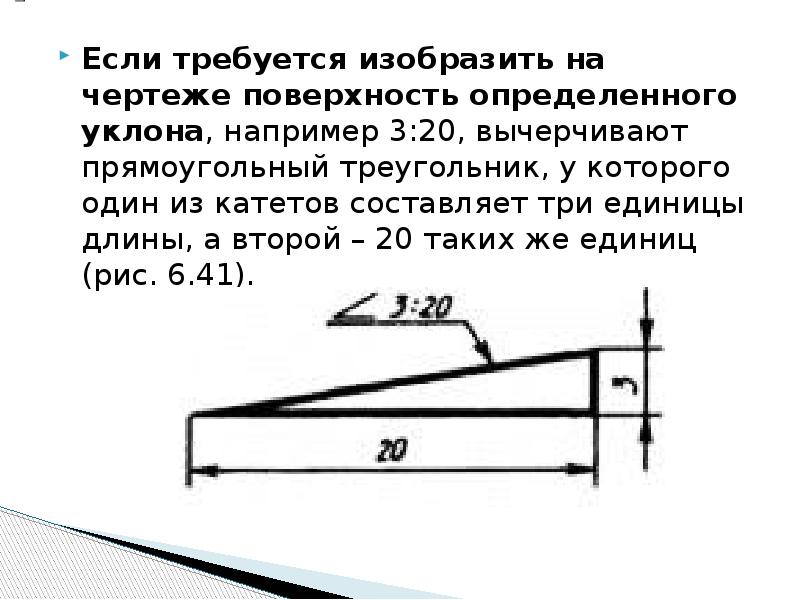 В чертежах металлорежущих инструментов часто конусность определяется надписью, указывающей номер конуса Морзе. В этих случаях размеры конических элементов устанавливают по ГОСТ 10079–71 и др.
В чертежах металлорежущих инструментов часто конусность определяется надписью, указывающей номер конуса Морзе. В этих случаях размеры конических элементов устанавливают по ГОСТ 10079–71 и др.
На чертежах конусность наносят согласно правилам ГОСТ 2.307–2011. Перед размерным числом, определяющим величину конусности, наносят условный знак в виде равнобедренного треугольника, острие которого направлено в сторону вершины конуса.
Знак и цифры, указывающие величину конусности, располагают на чертежах параллельно геометрической оси конического элемента.
Они могут быть проставлены над осью (рис. 6.39, 6 ) или на полке (рис. 6.39, в). В последнем случае полка соединяется с образующей конуса с помощью линии выноски, заканчивающейся стрелкой.
Уклон
Плоские поверхности деталей, расположенные наклонно, обозначают на чертеже величиной уклона. Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис. 6.40, б ). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100. Величина уклона клина будет 1:10.
Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис. 6.40, б ). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100. Величина уклона клина будет 1:10.
Рис. 6.40.
На чертеже уклоны указывают знаком и отношением двух чисел, например 1:50; 3:5.
Если требуется изобразить на чертеже поверхность определенного уклона, например 3:20, вычерчивают прямоугольный треугольник, у которого один из катетов составляет три единицы длины, а второй – 20 таких же единиц (рис. 6.41).
Рис. 6.41.
При вычерчивании деталей или при их разметке для построения линии по заданному уклону приходится проводить вспомогательные линии. Например, чтобы провести линию, уклон которой 1:4, через концевую точку вертикальной линии (рис. 6.42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию.
6.42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию.
Рис. 6.42.
Вершина знака уклона должна быть направлена в сторону наклона поверхности детали. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон.
И исполнению.
Конус Морзе и метрический конус
Конус Морзе — одно из самых широко применяемых креплений инструмента. Был предложен Стивеном А. Морзе приблизительно в 1864 году .
Конус Морзе подразделяется на восемь размеров, от КМ0 до КМ7 (англ. MT0-MT7 , нем. MK0-MK7 ) . Конусность от 1:19,002 до 1:20,047 (угол конуса от 2°51’26″ до 3°00’52″, уклон конуса от 1°25’43″ до 1°30’26″) в зависимости от типоразмера.
Метрический конус
По мере развития станкостроения понадобилось расширить диапазон размеров конусов Морзе как в большую, так и в меньшую стороны. При этом, для новых типоразмеров конуса, выбрали конусность ровно 1:20 (угол конуса 2°51’51″, уклон конуса 1°25’56″) и назвали их метрическими конусами (англ. Metric Taper
). Типоразмер метрических конусов указывается по наибольшему диаметру конуса в миллиметрах. ГОСТ 25557-2006 также определяет уменьшенные метрические конуса № 4 и № 6 (англ. ME4, ME6
) и большие метрические конуса № 80, 100, 120, 160, 200 (англ. ME80 — ME200
).
При этом, для новых типоразмеров конуса, выбрали конусность ровно 1:20 (угол конуса 2°51’51″, уклон конуса 1°25’56″) и назвали их метрическими конусами (англ. Metric Taper
). Типоразмер метрических конусов указывается по наибольшему диаметру конуса в миллиметрах. ГОСТ 25557-2006 также определяет уменьшенные метрические конуса № 4 и № 6 (англ. ME4, ME6
) и большие метрические конуса № 80, 100, 120, 160, 200 (англ. ME80 — ME200
).
Конструктивных различий между конусом Морзе и метрическим нет.
| Обозначение конуса | Конусность | D | D 1 | d | d 1 | d 2 | d 3 max | d 4 max | d 5 | l 1 max | l 2 max | l 3 max | l 4 max | l 5 min | l 6 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Метрический | № 4 | 1:20 | 4 | 4,1 | 2,9 | — | — | — | 2,5 | 3 | 23 | 25 | — | — | 25 | 21 |
| № 6 | 1:20 | 6 | 6,2 | 4,4 | — | — | — | 4 | 4,6 | 32 | 35 | — | — | 34 | 29 | |
| Морзе | КМ0 | 1:19,212 | 9,045 | 9,2 | 6,4 | — | 6,1 | 6 | 6 | 6,7 | 50 | 53 | 56,3 | 59,5 | 52 | 49 |
| КМ1 | 1:20,047 | 12,065 | 12,2 | 9,4 | M6 | 9 | 8,7 | 9 | 9,7 | 53,5 | 57 | 62 | 65,5 | 56 | 52 | |
| КМ2 | 1:20,020 | 17,780 | 18 | 14,6 | M10 | 14 | 13,5 | 14 | 14,9 | 64 | 69 | 75 | 80 | 67 | 62 | |
| КМ3 | 1:19,922 | 23,825 | 24,1 | 19,8 | M12 | 19,1 | 18,5 | 19 | 20,2 | 80,1 | 86 | 94 | 99 | 84 | 78 | |
| КМ4 | 1:19,254 | 31,267 | 31,6 | 25,9 | M16 | 25,2 | 25,2 | 24 | 26,5 | 102,5 | 109 | 117,5 | 124 | 107 | 98 | |
| КМ5 | 1:19,002 | 44,399 | 44,7 | 37,6 | M20 | 36,5 | 35,7 | 35,7 | 38,2 | 129,5 | 136 | 149,5 | 156 | 135 | 125 | |
| КМ6 | 1:19,180 | 63,348 | 63,8 | 53,9 | M24 | 52,4 | 51 | 51 | 54,6 | 182 | 190 | 210 | 218 | 188 | 177 | |
| КМ7 | 1:19,231 | 83,058 | — | 285. 75 75 | 294.1 | |||||||||||
| Метрический | № 80 | 1:20 | 80 | 80,4 | 70,2 | M30 | 69 | 67 | 67 | 71,5 | 196 | 204 | 220 | 228 | 202 | 186 |
| № 100 | 1:20 | 100 | 100,5 | 88,4 | M36 | 87 | 85 | 85 | 90 | 232 | 242 | 260 | 270 | 240 | 220 | |
| № 120 | 1:20 | 120 | 120,6 | 106,6 | M36 | 105 | 102 | 102 | 108,5 | 268 | 280 | 300 | 312 | 276 | 254 | |
| № 160 | 1:20 | 160 | 160,8 | 143 | M48 | 141 | 138 | 138 | 145,5 | 340 | 356 | 380 | 396 | 350 | 321 | |
| № 200 | 1:20 | 200 | 201 | 179,4 | M48 | 177 | 174 | 174 | 182,5 | 412 | 432 | 460 | 480 | 424 | 388 |
Укороченные конуса Морзе
Для многих применений длина конуса Морзе оказалась избыточной. Поэтому были придуманы девять типоразмеров укороченных конусов Морзе, полученных удалением более толстой части конуса Морзе. Цифра в обозначении короткого конуса — диаметр новой толстой части конуса в мм. Российский стандарт на укороченные конуса ГОСТ 9953-82 «Конусы инструментов укороченные. Основные размеры.».
Поэтому были придуманы девять типоразмеров укороченных конусов Морзе, полученных удалением более толстой части конуса Морзе. Цифра в обозначении короткого конуса — диаметр новой толстой части конуса в мм. Российский стандарт на укороченные конуса ГОСТ 9953-82 «Конусы инструментов укороченные. Основные размеры.».
- B7 — укороченный до 14 мм КМ0 .
- B10 , B12 — укороченный до 18 и 22 мм соответственно КМ1 .
- B16 , B18 — укороченный до 24 и 32 мм соответственно КМ2 .
- B22 , B24 — укороченный до 45 и 55 мм соответственно КМ3 .
- B32 — укороченный до 57 мм КМ4 .
- B45 — укороченный до 71 мм КМ5 .
Угол наклона, высота и уклон односкатной крыши: как выполнить расчет
В мире существуют тысячи архитектурных традиций внешнего вида крыш. В современной архитектуре довольно популярны односкатные формы крыш. Они идеально сочетаются с ландшафтным дизайном и многообразны в исполнении. Модный тренд пришел к нам из Австралии, где отсутствие снега позволяет творить с архитектурой жилых домов все, что диктует фантазия.
Модный тренд пришел к нам из Австралии, где отсутствие снега позволяет творить с архитектурой жилых домов все, что диктует фантазия.
Но в снежных регионах России такую крышу нужно строить только с соответствующим уклоном и в правильном направлении. Одним словом, главный параметр функциональности – угол наклона односкатной крыши. Как правильно его рассчитать вы узнаете из нашей статьи.
Чтобы у вас было общее представление об односкатных кровлях, посмотрите это видео:
Первым делом рассчитайте нагрузки на односкатную крышу. Их принято делить на постоянные и динамические. Первые – это вес кровельного покрытия, которое всегда находится на крыше, а также антенны, ТВ-тарелки, дымоход и прочее. Т.е. все то, что будет на кровле и днем, и ночью.
А динамические нагрузки, или, как их еще называют, переменные, – это те, что бывают время от времени: снег, град, человек, ремонтные материалы и инструменты. А еще ветер, который может срывать односкатные крыши ввиду их парусности. Рассмотрим их подробнее.
А еще ветер, который может срывать односкатные крыши ввиду их парусности. Рассмотрим их подробнее.
Снеговые нагрузки
Давление снега также зависит от угла наклона. К примеру, для Московского региона при скате кровли в 30℃ нагрузка составит порядка 130 кг/кв.м.
А если сделать кровлю круче 45°, снег с большой вероятностью не сможет на ней задерживаться, но это зависит от шероховатости кровельного покрытия. Для средней полосы России, где снегопады умеренные, односкатную крышу достаточно делать в пределах 35-30°:
Минимальный угол, который должен быть, чтобы снег смог сходить с односкатной кровли сам – это 15°. А максимальный – 60°, делать крышу более крутой нет смысла.
Ветровые нагрузки
В регионах с сильными ветрами крышу с большим уклоном может легко сорвать. В этом случае плоскость ската лучше обращать к наветренной стороне. Но и слишком пологую кровлю не стоит делать по той же причине.
Комбинированные нагрузки
Обязательно рассчитайте для односкатной крыши такое значение, как сочетание максимально неблагоприятных постоянных и временных нагрузок.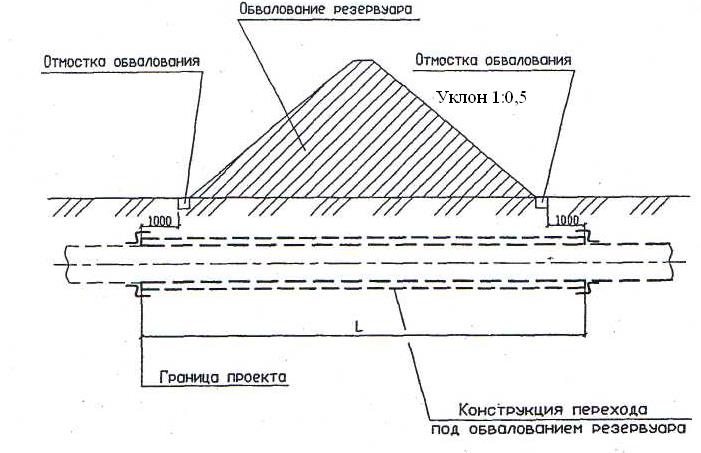 Т.е. критическую точку, которую должна выдерживать стропильная система.
Т.е. критическую точку, которую должна выдерживать стропильная система.
К примеру, вам придется в сильную бурю и снегопад выйти на крышу, да не одному, а с помощником. Выдержит ли ваша конструкция одновременно и снег, и ветер, и двух человек? Лучше знать об этом заранее.
Уклон односкатной крыши – в довольно широком диапазоне: от 6° до 60°. Все зависит от местности, в которой вы собрались строиться: если вам нужно сбрасывать тонны снега с крыши каждую зиму, тогда делайте скат покруче, если планируете защититься от ветра – более пологий. Кроме того, при определенном угле односкатная крыша направляет поток воздуха в нужном направлении, захватывая осадки и отводя их. Помните об этом!
Крутые односкатные крыши
Чем больше угол односкатной крыши, тем быстрее по ней стекает вода. Здесь не будут задерживаться ни листья, ни грязь, а потому само кровельное покрытие прослужит намного дольше. Кроме того, на такой кровле лучше заметна визуальная эстетика выбранной черепицы или металлопрофиля, что часто играет немалую роль для владельцев дома.
Малоуклонные односкатные крыши
Скорость стекающей дождевой и талой воды на малоуклонных скатах намного ниже, а потому есть риск застаивания воды, скопления грязи и застревания льда. На таких кровлях быстро развивается мох и налипает листва. Особенно, если кровельное покрытие шероховатое.
Главное требование к кровле — чтобы вода при таянии снега или после дождя не оставалась на поверхности кровельного материала, а легко скатывалась. Если же она имеет слишком низкий уклон, то влага будет подолгу стоять во всех неровностях и швах. И чем дольше – тем больше у нее шансов проникнуть внутрь и создать много проблем в виде сырости, испортившегося утеплителя и коррозии металлических элементов кровли:
Но есть и свои плюсы: чем меньше угол наклона односкатной крыши, тем более близка геометрия внутренних помещений к традиционному кубу. А, значит, воспринимается легче и используется с большей пользой.
Однако в этом случае нужно тщательно позаботиться о ее гидроизоляции, чтобы талые и дождевые воды не смогли проникнуть в стропильную систему.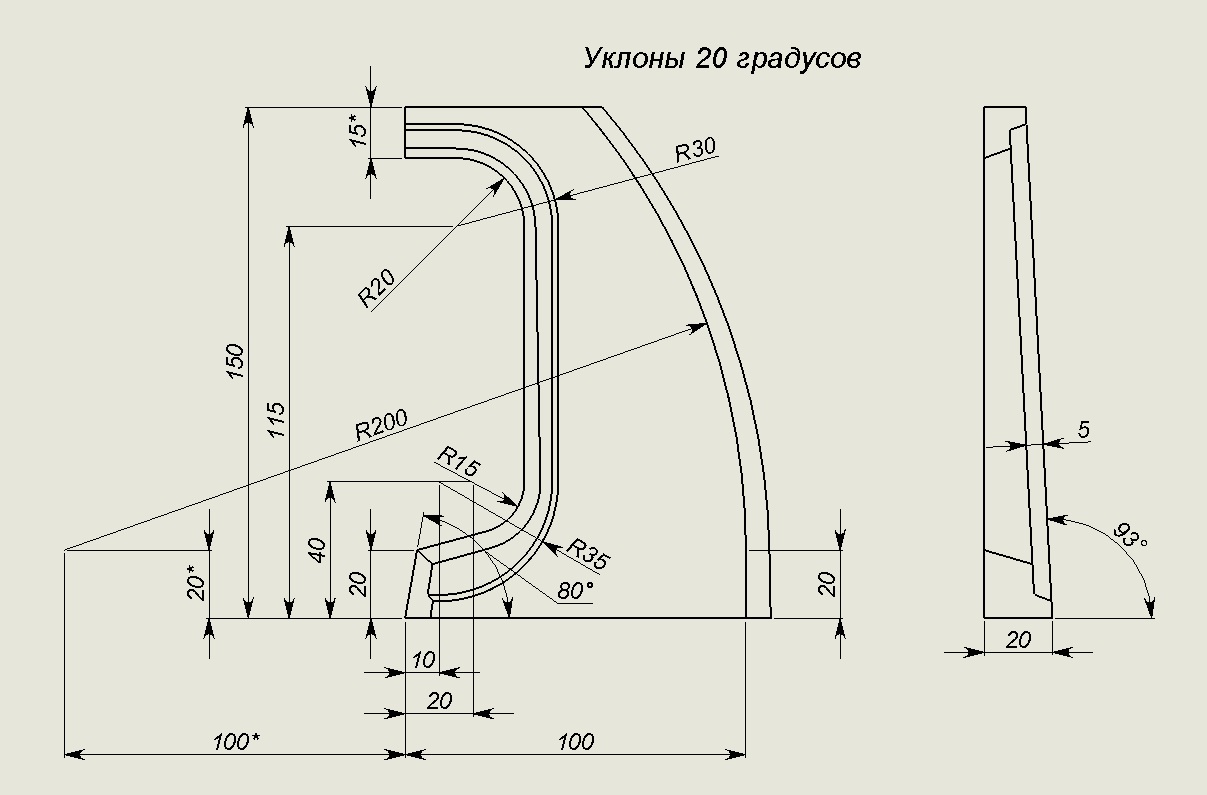 Необходимы такие кровельные покрытия, как мембраны, рулонная изоляция или цельные листы.
Необходимы такие кровельные покрытия, как мембраны, рулонная изоляция или цельные листы.
Со стандартным углом наклона односкатная кровля строится так:
Минимальный угол односкатной крыши
Односкатную крышу, угол которой всего 3-5° или совершенно плоскую, нередко делают инверсионной. От обычной кровли она отличается тем, что внутренняя многослойная начинка пирога формируется в строго противоположном порядке. А в качестве кровельного покрытия используют материалы с высокой стойкостью к физическим нагрузкам и к истиранию. На такой кровле часто устраивают веранды, сады или зоны отдыха.
В функциональном плане односкатные крыши делят на три основных типа: вентилируемые, невентилируемые и комбинированные. Рассмотрим каждый вариант подробнее.
Вентилируемая конструкция
Такие обустраивают в строениях закрытого типа. В качестве вентиляции служат продухи и специальные пустоты между изоляционными слоями, через которые воздух, проходя, захватывает капельки влаги из утеплителя и выносит их наружу.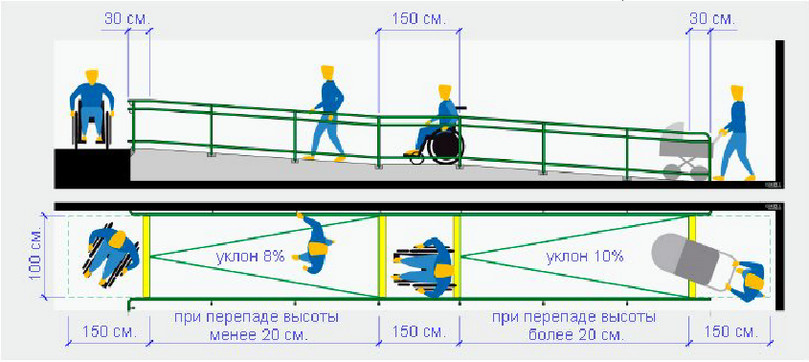
Если такой вентиляции не обеспечить, тогда влага будет оставаться внутри утеплителя (а она все равно в него попадает, хоть и понемногу), и утеплитель начнет отсыревать, портиться. И в итоге разрушаться будет постепенно весь кровельный пирог.
Невентилируемая конструкция
Этот тип односкатной крыши преимущественно встречается на террасах и хозпостройках. Обычно угол такой крыши находится в интервале всего 3-6°, хотя никаких ограничений к нему нет.
Вентиляция в таких крышах не нужна потому, что воздух в помещении без стен или с часто открытыми широкими дверьми (как в случае с гаражом) и сам хорошо вентилирует, унося на улицу любые водяные пары. Которых, к слову, и так почти не образовываются в подобных постройках:
Углом односкатной крыши принято называть угол, под которым стропила и скат крыши наклонены к горизонтальной плоскости потолка. Причем отнеситесь серьезно к этой схеме, если вы хотите обеспечить вашей крыше правильную механическую прочность:
Угол наклона скатов измеряется в процентах и градусах. Но, если с градусами еще более-менее понятно (спасибо школьному курсу геометрии), то что такое проценты? Проценты – это отношение разницы высоты конька и карниза к горизонтали ската, умноженное на 100.
Но, если с градусами еще более-менее понятно (спасибо школьному курсу геометрии), то что такое проценты? Проценты – это отношение разницы высоты конька и карниза к горизонтали ската, умноженное на 100.
Есть еще один интересный момент: многие архитекторы специально рассчитывают угол односкатной кровли так, чтобы он был равен углу возвышения солнца в данной местности в середине весны. Тогда можно до миллиметра рассчитать, когда и какая будет тень, что важно для планирования террас перед домом и других мест отдыха.
Свои требования к минимальному и максимальному углу наклона односкатной кровли имеют и современные кровельные материалы:
- Профнастил: min 8°- max 20°.
- Фальцевая кровля: min 18°- max 30°.
- Шифер: min 20°- max 50°.
- Мягкая кровля: min 5°- max 20°.
- Металлочерепица: min 30° — max 35°.
Конечно, чем меньше угол, тем более дешевые материалы вы можете применять: рубероид, профнастил и подобные им.
Вы удивитесь, но специально для малоуклонных кровель сегодня разрабатывают те же виды кровельного покрытия, что обычно используются при наклоне не менее 30°. Зачем? Такова мода в Германии, которая дошла и до нас: односкатная крыша почти пологая, а кровля – стильная. Но как? Просто производители улучшают качество замков, делают больше область нахлеста и тщательнее продумывают защиту от грязи. Вот и все хитрости.
Зачем? Такова мода в Германии, которая дошла и до нас: односкатная крыша почти пологая, а кровля – стильная. Но как? Просто производители улучшают качество замков, делают больше область нахлеста и тщательнее продумывают защиту от грязи. Вот и все хитрости.
А от выбранного угла наклона крыши и планируемых на ее нагрузок определяемся с видом крепления стропил к стенам. Так, всего таких видов три: висячие стропила, наслонные и скользящие.
Висячие стропила
Висячие стропила – единственный вариант, когда соединение должно быть жестким, но для стропил между боковыми опорами нет возможности сделать опору.
Проще говоря, у вас есть только внешние несущие стены, и никаких перегородок внутри. Скажем, это довольно сложная стропильная система, и к ее строительству нужно подходить с ответственностью. Вся проблема в больших пролетов и в давлении, которое оказывается на стены:
Или как в этом проекте:
Наслонные стропила
Здесь уже вся крыша давит минимум на три опоры: две внешние стены и одну внутреннюю.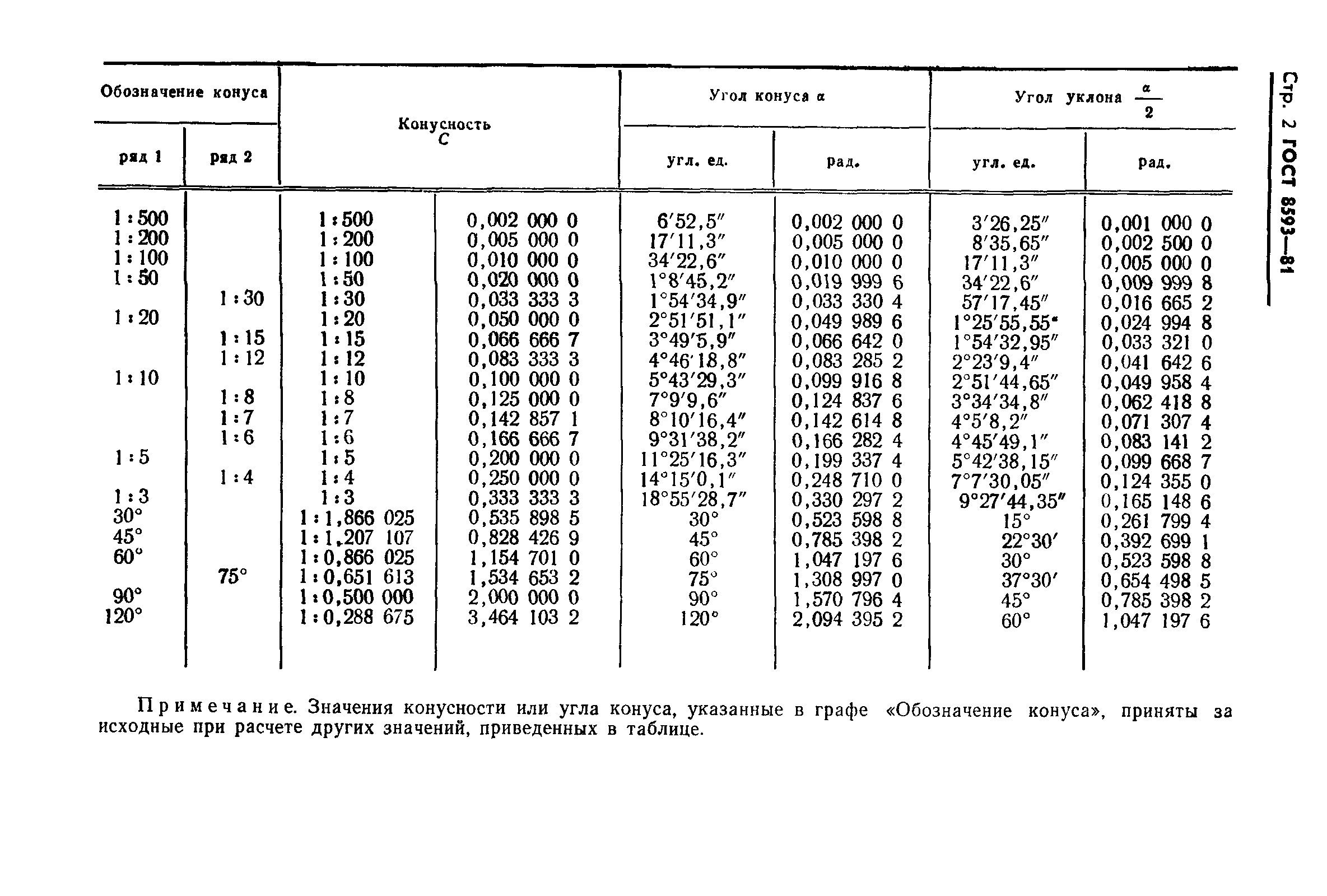 А сами стропила здесь используются плотные, с сечением не менее 5х5 см брусков и 5х15 см стропильных ног.
А сами стропила здесь используются плотные, с сечением не менее 5х5 см брусков и 5х15 см стропильных ног.
Скользящие стропила
В этой стропильной системе в качестве одной из опор служит бревно в коньке. И для соединения с ним стропил используются такие специальные элементы, как «скользячки». Это металлические элементы, которые помогают стропилу при усадке стен немного двигаться вперед, чтобы избежать трещин. Совсем немного! И благодаря этому устройству крыша легко переносит даже достаточно ощутимую усадку сруба, без каких-либо повреждений.
Суть проста: чем больше в стропильной системе узлов, тем она гибче и прочнее. Тем больше односкатная крыша способна выдерживать давление веса кровельного покрытия и снега, и при этом не ломаться. Но есть стропильные системы, где соединение вообще статично:
Вот три самых популярных способа точно вычислить нужную высоту будущей крыши.
Способ №1. Геометрический
Односкатная крыша имеет вид прямоугольного треугольника. Длина стропильной ноги в этом треугольнике – гипотенуза. А, как вы помните из школьного курса геометрии, длина гипотенузы равна корню из суммы квадратов катетов.
Длина стропильной ноги в этом треугольнике – гипотенуза. А, как вы помните из школьного курса геометрии, длина гипотенузы равна корню из суммы квадратов катетов.
Способ №2. Тригометрический
Еще один вариант расчета длины стропильных ног такой:
- Обозначим А длину стропильных балок.
- Обозначим Б длину стропил от стены до конька, или длину части стены в этой области (если стены вашей постройки разной высоты).
- Обозначим Х длину стропил от конька до края противоположной стены.
В этом случае Б = А * tgY, где Y – это угол наклона крыши, а длина ската высчитывается так:
Х = А / sin Y
На самом деле все это не сложно – просто подставьте нужные значения, и вы получите все параметры будущей крыши.
Способ №3. Онлайн-калькуляторы
Кстати, рассчитать нужный угол односкатной крыши помогут также современные онлайн-калькуляторы. Обычно их настраивают под действующие СНиПы – «Нагрузка и воздействие» ТКП 45-5. 05. Но этот метод можно использовать только как дополнительный.
05. Но этот метод можно использовать только как дополнительный.
Вычислили? А теперь переходим к строительству самой крыши:
Надеемся, что вы во всем разобрались легко!
Калькулятор уклона
По определению наклон или уклон линии описывает ее крутизну, наклон или уклон. Где м — уклон |
Если известны 2 точки
Если известна 1 точка и наклон
Уклон, иногда называемый в математике градиентом, представляет собой число, которое измеряет крутизну и направление линии или участка линии, соединяющей две точки, и обычно обозначается как м .Как правило, крутизна линии измеряется абсолютным значением ее уклона, м . Чем больше значение, тем круче линия. Имея м , можно определить направление линии, которую описывает м на основе ее знака и значения:
- Линия увеличивается и идет вверх слева направо, когда m > 0
- Линия убывает и идет вниз слева направо, когда m < 0
- Линия имеет постоянный наклон и является горизонтальной, когда m = 0
- Вертикальная линия имеет неопределенный наклон, так как в результате получится дробь со знаменателем 0.
 См. приведенное ниже уравнение.
См. приведенное ниже уравнение.
Уклон — это, по сути, изменение высоты по сравнению с изменением горизонтального расстояния, и его часто называют «подъемом над уклоном». Он применяется в градиентах в географии, а также в гражданском строительстве, например, при строительстве дорог. В случае дороги «подъем» — это изменение высоты, а «пробег» — это разница в расстоянии между двумя фиксированными точками, если расстояние для измерения недостаточно велико, чтобы кривизна земли была рассматривается как фактор.Наклон представлен математически как:
В приведенном выше уравнении y 2 — y 1 = Δy или изменение по вертикали, а x 2 — x 1 = Δx или изменение по горизонтали, как показано на графике. Также можно видеть, что Δx и Δy — это отрезки, образующие прямоугольный треугольник с гипотенузой d , где d — это расстояние между точками (x 1 , y 1 , y
7
1 ) и (х 2 , у 2 ) .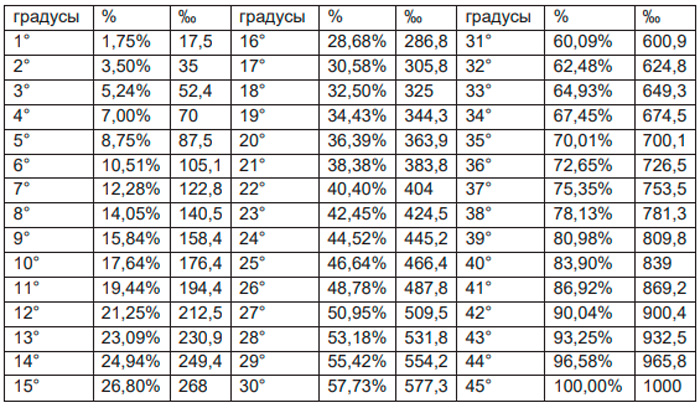 Поскольку Δx и Δy образуют прямоугольный треугольник, можно вычислить d по теореме Пифагора. Обратитесь к Калькулятору треугольника для получения более подробной информации о теореме Пифагора, а также о том, как рассчитать угол наклона θ , представленный в калькуляторе выше. Кратко:
Поскольку Δx и Δy образуют прямоугольный треугольник, можно вычислить d по теореме Пифагора. Обратитесь к Калькулятору треугольника для получения более подробной информации о теореме Пифагора, а также о том, как рассчитать угол наклона θ , представленный в калькуляторе выше. Кратко:
d = √(х 2 — х 1 ) 2 + (у 2 — у 1 ) 2
Вышеприведенное уравнение в корне является теоремой Пифагора, где гипотенуза d уже решена, а две другие стороны треугольника определяются вычитанием двух значений x и y , заданных двумя точками .Имея две точки, можно найти θ , используя следующее уравнение:
м = тангенс (θ)
Учитывая точки (3,4) и (6,8), найдите наклон линии, расстояние между двумя точками и угол наклона:
d = √(6 — 3) 2 + (8 — 4) 2 = 5
Хотя это выходит за рамки этого калькулятора, помимо его основного линейного использования, понятие наклона важно в дифференциальном исчислении. Для нелинейных функций скорость изменения кривой варьируется, а производная функции в данной точке — это скорость изменения функции, представленная наклоном линии, касательной к кривой в этой точке.
Для нелинейных функций скорость изменения кривой варьируется, а производная функции в данной точке — это скорость изменения функции, представленная наклоном линии, касательной к кривой в этой точке.
Измерение уклона и уклона крыши
by Nick Gromicko, CMI® and Benjamin GromickoИ шаг, и наклон указывают на наклон крыши, выраженный как пропорция вертикали к горизонтали. В этой статье описывается как уклон крыши, так и уклон крыши, а также различия между ними, поскольку они не совпадают. Поскольку уклон влияет на то, как устанавливаются кровельные системы, в том числе определяет, какой тип материала кровельного покрытия может быть применен, понимание того, как измерить уклон крыши, может быть ценным для домашнего инспектора.
На приведенном выше рисунке показана простая двускатная крыша и общее соотношение подъема, пролета и пролета. Каркас крыши представляет собой практическое применение геометрии, а уклон крыши в значительной степени основан на свойствах прямоугольного треугольника.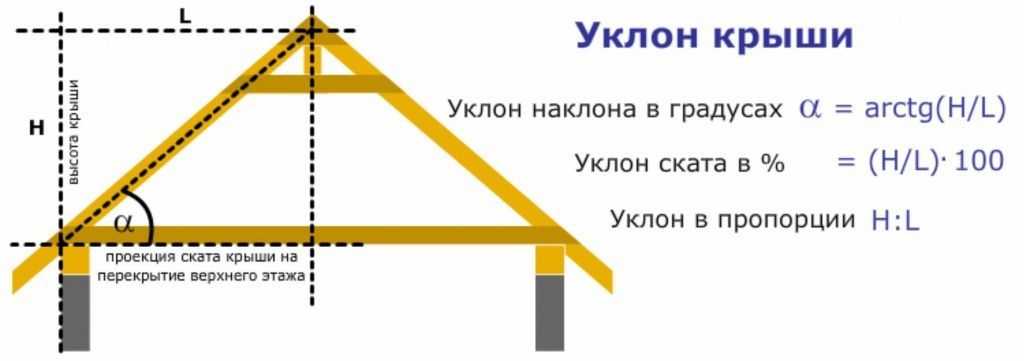
В каркасе крыши основание прямоугольного треугольника называется прогоном. Пробег — это расстояние от внешней стороны верхней пластины стены до точки, расположенной непосредственно под центром конька. Вертикальная сторона треугольника называется подъемом и представляет собой расстояние, на которое стропильная доска поднимается вверх над верхней пластиной стены.
Уклон
Уклон – это уклон крыши, выраженный как отношение вертикального подъема к горизонтальному прогону, где прогон – это некоторая часть пролета. Это соотношение всегда выражается в дюймах на фут.
Коэффициент уклона
Говорят, что крыша, которая поднимается на 4 дюйма на каждый 1 фут или 12 дюймов пробега, имеет уклон «4 из 12». Если подъем составляет 6 дюймов на каждые 12 дюймов пробега, то уклон крыши равен «6 из 12». Наклон может быть выражен численно в виде отношения.Коэффициент уклона представляет собой определенный подъем по вертикали на каждые 12 дюймов горизонтального участка.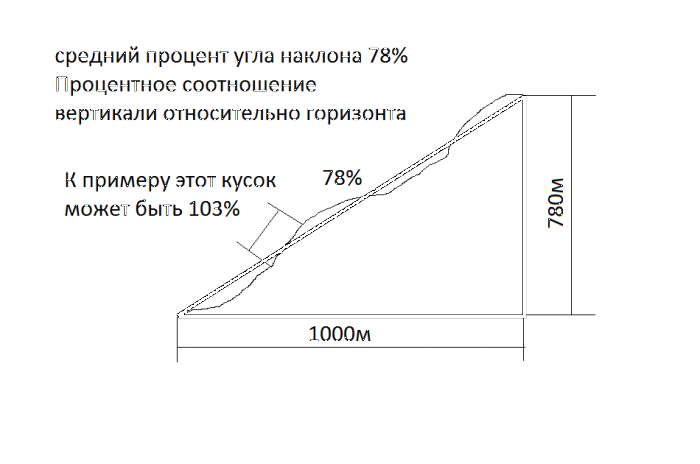 Например, наклон «4 из 12» можно выразить как отношение 4:12. Наклон «6 из 12» выражается как 6:12.
Например, наклон «4 из 12» можно выразить как отношение 4:12. Наклон «6 из 12» выражается как 6:12.
Треугольный символ над линией крыши на этом архитектурном фасаде предоставляет информацию о склоне .
- как соотношение; и
- в дюймах на фут.
Уклон
Доля ската
Исторически слово «скат» означало отношение высоты конька ко всему пролету/ширине здания или отношение длины стропил к ширине здания. А тогда конек обычно находился посередине пролета.В современной строительной практике это уже не так. Конек может быть размещен в любом месте пролета, от середины до любой конечной точки пролета.
Крыша, возвышающаяся на 8 футов над 24-футовым пролетом, имеет уклон «от 1 до 3».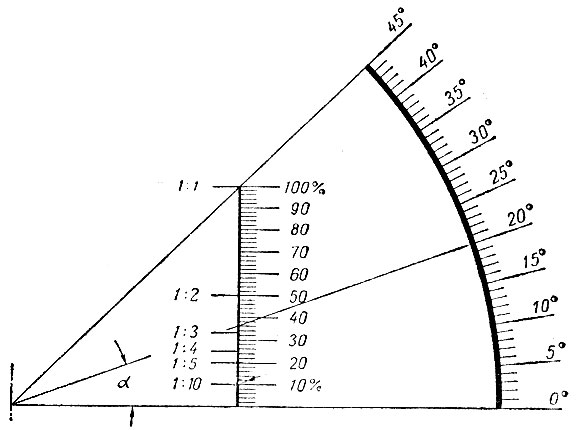 Если подъем составляет 4 фута над 24-футовым пролетом, то уклон крыши считается «от 1 до 6».
Если подъем составляет 4 фута над 24-футовым пролетом, то уклон крыши считается «от 1 до 6».
Шаг может быть выражен численно в виде дроби. Доля шага представляет собой определенную величину вертикального подъема по всему пролету. Например, для крыши с подъемом 4 фута и пролетом 24 фута шаг составляет «от 1 до 6», что может быть выражено как доля 1/6.Шаг «от 12 до 24» выражается как 1/2.
Термины «шаг» и «наклон» часто используются взаимозаменяемо, что неверно. Они не означают одно и то же. А наклон дает более ценную информацию, чем шаг, как определено в этой статье.
Используя приведенную выше иллюстрацию и информацию, которую мы только что узнали об уклоне и уклоне, мы видим, что уклон 2:12 можно выразить как шаг 1/12, предполагая, что пролет в два раза превышает длину участка. Если уклон составляет 4:12, шаг для 24-футового пролета составляет 1/6.Если шаг 1/3, наклон 8:12. Помните, уклон выражается в виде отношения и в дюймах на фут. А шаг – это дробь, полученная путем деления подъема на весь пролет.

Минимальный уклон для различных кровельных покрытий
Международный жилищный кодекс (IRC) устанавливает минимальные требования к кровельным покрытиям и предписывает использование инструкций по установке кровельного покрытия от производителя.
- Битумная черепица должна укладываться на скаты крыши 2:12 или больше (2015 IRC R905.2.2).
- Глиняная и бетонная черепица должна укладываться на скаты крыши 2,5:12 или больше (2015 IRC R905.3.2).
- Металлическая черепица должна укладываться на скате крыши 3:12 или больше (2015 IRC R905.4.2).
- Рулонная кровля с минеральной поверхностью должна укладываться на скаты крыши 1:12 или больше (2015 IRC R905.4.2).
- Сланцевая черепица должна укладываться на скаты крыши 4:12 или больше (2015 IRC R905.6.2).
- Деревянная черепица должна укладываться на скаты крыши 3:12 или больше (2015 IRC R905.7.2).
- Деревянные распорки следует устанавливать на скатах крыши 3:12 или больше (2015 IRC R905.
 8.2).
8.2). - Сборные крыши должны быть установлены на скате крыши 0,25:12 или больше (2015 IRC R905.9.1), за исключением сборных крыш из каменноугольной смолы, которые имеют минимальный уклон крыши в одну восьмую по вертикали и 12 единиц по горизонтали (уклон 1%).
- Металлические кровельные панели должны быть установлены на скатах крыши в соответствии с определенными швами (2015 IRC R905.10.2):
- минимальный уклон крыши 3:12 для металлических крыш с непропаянными швами внахлест без нанесения герметика внахлест
- минимальная крыша наклон 0.5:12 для металлических крыш с непаянным фальцем внахлестку с нанесенным герметиком внахлест (IRC R905.11.1, 2015 г.).
- Однослойная кровля из термореактивного материала должна укладываться на скате крыши 0,25:12 или больше (2015 IRC R905.12.1).
- Однослойная кровля из термопласта должна укладываться на скатах крыши 0,25:12 или больше (2015 IRC R905.13.1).
- Кровля из напыляемого пенополиуретана должна укладываться на скате крыши 0,25:12 или больше (2015 IRC R905.
 14.1).
14.1). - Жидкая кровля должна укладываться на скаты крыши 0,25:12 или больше (2015 IRC R905.15.1).
- Фотогальваническая черепица должна укладываться на скаты крыши 2:12 или больше (2015 IRC R905.16.2).
Битумная черепица
Уклон крыши влияет на поверхностный сток воды и может определить тип кровельных материалов, которые следует укладывать.Битумную черепицу следует использовать только на крышах с уклоном 2:12 или больше. Крыши из битумной черепицы предназначены для отвода воды, а не в качестве водонепроницаемого барьера. Уклон крыши влияет на ее способность отводить воду и определяет пределы использования битумной черепицы.
Большинство битумных гонтов можно использовать на скатах крыш от 4:12 до 21:12, используя стандартные методы укладки. Асфальтовую черепицу можно использовать на уклонах от 2:12 до 3,9:12, если соблюдаются специальные процедуры укладки на малых уклонах.Инспектор обычно находит рулонные кровельные материалы, установленные на уклонах менее 4:12.
Измерение уклона
Вам понадобится столярный уровень, рулетка и карандаш.
Отмерьте 12 дюймов от одного конца уровня и сделайте отметку.
Замеры можно производить с незавершенного чердачного помещения под кровлей или в районе скоса, или поверх кровельных материалов. Измерение уклона от поверхности крыши может быть не самым точным из-за изначально неровной поверхности кровельного покрытия.
Ползите на недостроенный чердак. Найдите легкодоступную доску для стропил крыши. Приложите конец уровня к нижнему краю стропила крыши и держите его идеально ровно. Измерьте от 12-дюймовой отметки на уровне по вертикали до нижнего края стропила. Это измерение представляет собой количество дюймов, на которые поднимается крыша за 12 дюймов.
Найдите легкодоступную доску для граблей. Держите столярный уровень идеально ровно, удерживая его конец у нижнего края доски граблей.Измерьте от 12-дюймовой отметки на уровне по вертикали до того места, где рулетка касается нижнего края доски граблей.
 Это измерение представляет собой количество дюймов, на которые поднимается крыша за 12 дюймов.
Это измерение представляет собой количество дюймов, на которые поднимается крыша за 12 дюймов.Измерение уклона крыши от поверхности крыши будет неточным без использования чего-либо, чтобы сделать плоскую поверхность, от которой будет измеряться уклон. Использование 48-дюймового столярного уровня или прямой доски 2×4 может оказаться полезным для создания гладкой поверхности, отражающей наклон крыши.
Инспектор может счесть полезным использование мобильных технологий. Существуют приложения для мобильных устройств, которые точно измеряют уклон крыши, в том числе с возможностью делать цифровые снимки уклона с земли.
РезюмеШаг и наклон не означают одно и то же. Уклон – это отношение, измеряемое в дюймах на фут. Поскольку уклон влияет на то, как вода сбрасывается с поверхности крыши, и определяет пределы использования битумной черепицы, понимание того, как измерить уклон крыши, может быть ценным для домашнего инспектора.

Уклон Против. Шаг
Во время написания нашего последнего поста ко мне пришел интересный вопрос. Это был тот же вопрос, который у меня возник, когда я получил манометр Holts Roof Gauge после покупки его на eBay и начал внимательно его рассматривать. В чем разница между наклоном и шагом? 1/4 шага — это наклон 6:12? Шаг 7/12 — наклон 14:12? Что, черт возьми, здесь происходит? Я занимаюсь кровельными работами уже 35 лет, и уклон и уклон всегда значили для меня одно и то же.
Ну, это отправило меня в интернет. Мне нравится думать, что я хороший гуглер, поэтому я очень много думал о том, какие условия поиска лучше всего использовать, и пришел к выводу: «В чем разница между уклоном крыши и уклоном крыши». Я же говорил вам, что я хороший гуглер. Я нажал Enter, и вуаля, мой вопрос был решен.
Здравствуйте, мистер НАЧИ (это Национальная ассоциация сертифицированных домашних инспекторов для тех, кто не является вашим другом). На сайте NACHI есть супер-пупер хороший ответ на мой вопрос.
 Конечно, статья NACHI больше ориентирована на черепицу, а Mule-Hide больше не производит черепицу, но информация о соотношении уклона и уклона так же актуальна и для крыш с малым уклоном.
Конечно, статья NACHI больше ориентирована на черепицу, а Mule-Hide больше не производит черепицу, но информация о соотношении уклона и уклона так же актуальна и для крыш с малым уклоном.Вот что они сказали:
Наклон
Уклон – это уклон крыши, выраженный как отношение вертикального подъема горизонтального прогона, где прогон – это некоторая часть пролета. Это соотношение всегда выражается в дюймах на фут.
Коэффициент наклона
Говорят, что крыша, которая поднимается на 4 дюйма на каждые 1 фут или 12 дюймов пробега, имеет уклон «4 из 12».Если подъем составляет 6 дюймов на каждые 12 дюймов пробега, то уклон крыши составляет «6 из 12».
Наклон может быть выражен численно в виде отношения. Коэффициент уклона представляет собой определенное количество подъема по вертикали на каждые 12 дюймов горизонтального участка. Например, наклон «4 из 12» можно выразить как отношение 4:12. Наклон «6 из 12» выражается как 6:12.

Наклон выражается:
- как соотношение; и
- в дюймах на фут
Шаг
Уклон — это наклон крыши, выраженный в виде доли, полученной путем деления подъема на пролет, где пролет крыши — это расстояние между наружной поверхностью верхней плиты одной стены и другой.
Доля шага
Исторически слово «скат» означало отношение высоты конька ко всему пролету/ширине здания или отношение длины стропил к ширине здания. А тогда конек обычно находился посередине пролета. В современной строительной практике это уже не так. Конек может быть размещен в любом месте пролета, от середины до любой конечной точки пролета.
Говорят, что крыша, которая возвышается на 8 футов над 24-футовым пролетом, имеет уклон «от 1 до 3».Если подъем составляет 4 фута при пролете 24 фута, то говорят, что уклон крыши составляет «от 1 до 6».
Шаг может быть выражен численно в виде дроби. Доля шага представляет собой определенную величину вертикального подъема по всему пролету.
 Например, для крыши высотой 4 фута и пролетом 24 фута шаг равен «от 1 до 6», что можно выразить как дробь 1/6. Шаг «от 12 до 24» выражается как 1/2.
Например, для крыши высотой 4 фута и пролетом 24 фута шаг равен «от 1 до 6», что можно выразить как дробь 1/6. Шаг «от 12 до 24» выражается как 1/2.Итак, что я узнал? Я не думаю, что смогу сказать это лучше, чем статья NACHI:
«Термины «шаг» и «наклон» часто используются взаимозаменяемо, что неверно.Они не означают одно и то же. А наклон дает более ценную информацию, чем шаг, как определено в этой статье».
Еще раз спасибо NACHI.org и вот ссылка на всю статью: https://www.nachi.org/roof-slope-pitch.htm
Вернуться к блогуКалькулятор уклона
Использование калькулятора
Наклон линии — это ее вертикальное изменение, деленное на ее горизонтальное изменение, также известное как превышение над бегом.Когда у вас есть 2 точки на линии на графике, наклон представляет собой изменение y, деленное на изменение x.

Наклон линии — это мера ее крутизны.
Решения для расчета уклона
Введите две точки, используя числа, дроби, смешанные числа или десятичные дроби. Калькулятор уклона показывает работу и дает следующие решения уклона:
- Уклон м с двумя точками
- График линии для y = mx + b
- Форма уклона точки y — y 1 = m(x — x 1 )
- Форма пересечения наклона y = mx + b
- Стандартная форма Ax + By = C
- y-отрезок, когда x = 0
- x-пересечение, когда y = 0
Вам также будет предоставлена настраиваемая ссылка на Калькулятор средней точки, который решит и покажет работу, чтобы найти среднюю точку и расстояние для заданных двух точек.
Как рассчитать наклон линии
Расчет уклона, м по формуле для уклона:
Формула уклона
\[ m = \dfrac {(y_{2} — y_{1})} {(x_{2} — x_{1})} \] \[ m = \dfrac{rise}{run} = \dfrac{ \Delta y}{\Delta x} = \dfrac{y_2 — y_1}{x_2 — x_1} \]Здесь вам нужно знать координаты 2 точек на линии, (x 1 , y 1 ) и (x 2 , y 2 ).

Как найти наклон линии
- Найти разницу между координатами y, Δy — изменение y
- Найдите разницу между координатами x, Δx — это изменение x
- Разделите Δy на Δx, чтобы найти уклон
Δу = у 2 — у 1
Δх = х 2 — х 1
м = Δy/Δx
Пример: найти уклон
Допустим, вы знаете две точки на прямой и их координаты (2, 5) и (9, 19).Найдите наклон, найдя разницу в точках y, и разделите ее на разницу в точках x.
- Разница между координатами y Δy составляет
- Разница между координатами x Δx равна
- Разделите Δy на Δx, чтобы найти уклон м
Δу = у 2 — у 1
Δy = 19 — 5
Δy = 14
Δх = х 2 — х 1
Δx = 9 — 2
Δx = 7
\( м = \dfrac {14} {2} \)
\(м = 7 \)
Уравнения линий с наклоном
Существует 3 распространенных способа записи линейных уравнений с наклоном:
- Форма точечного откоса
- Форма пересечения уклона
- Стандартная форма
Форма точечного откоса записывается как
у — у 1 = м (х — х 1 )
Используя координаты одной из точек на линии, вставьте значения в точки x1 и y1, чтобы получить уравнение линии в форме точечного наклона.

Давайте используем точку из исходного примера выше (2, 5) и наклон, который мы рассчитали как 7. Поместите эти значения в формат наклона точки, чтобы получить уравнение этой линии в форме наклона точки:
у — 5 = 7(х — 2)
Если вы упростите приведенное выше уравнение наклона точки, вы получите уравнение линии в форме пересечения наклона.
Форма пересечения наклона записывается как
у = м х + б
Возьмите уравнение формы наклона точки и умножьте 7 на x и 7 на 2.
у — 5 = 7(х — 2)
у — 5 = 7х — 14
Продолжайте работать над уравнением так, чтобы у было по одну сторону от знака равенства, а все остальное по другую сторону.
Добавьте 5 к обеим частям уравнения, чтобы получить уравнение в форме пересечения наклона:
у = 7х — 9
Стандартная форма уравнения для линии записывается как
Топор + В = С
В некоторых ссылках вы также можете встретить стандартную форму, записанную как Ax + By + C = 0.

Используйте либо формулу формы точки наклона, либо уравнение формы точки пересечения наклона и выполните математические расчеты, чтобы преобразовать уравнение в стандартную форму. Обратите внимание, что уравнение не должно включать дроби или десятичные знаки, а коэффициент x должен быть только положительным.
Форма пересечения наклона: y = 7x — 9
Вычтите y из обеих частей уравнения, чтобы получить 7x — y — 9 = 0
Добавьте 9 к обеим частям уравнения, чтобы получить 7x — y = 9
Форма пересечения наклона y = 7x — 9 становится 7x — y = 9, записанной в стандартной форме.
Найти наклон по уравнению
Если у вас есть уравнение для прямой, вы можете представить его в форме пересечения наклона. Коэффициент x будет наклоном.
Пример
У вас есть уравнение прямой, 6x — 2y = 12, и вам нужно найти наклон.

Ваша цель — преобразовать уравнение в формат пересечения наклона y = mx + b
- Начните с вашего уравнения 6x — 2y = 12
- Добавьте 2y к обеим сторонам, чтобы получить 6x = 12 + 2y
- Вычтите 12 из обеих частей уравнения, чтобы получить 6x — 12 = 2y
- Вы хотите получить y в одной части уравнения, поэтому вам нужно разделить обе части на 2, чтобы получить y = 3x — 6
- Это форма пересечения наклона, y = 3x — 6.Наклон — это коэффициент x, поэтому в этом случае наклон = 3 .
Как найти точку пересечения оси Y
Точка пересечения линии с осью y представляет собой значение y, когда x=0. Это точка пересечения прямой с осью Y.
Используя уравнение y = 3x — 6, установите x=0, чтобы найти точку пересечения с осью y.
у = 3(0) — 6
г = -6
Y-пересечение равно -6
Как найти x-Intercept
Пересечение линии по оси X равно значению x, когда y=0.
 Это точка пересечения прямой с осью x.
Это точка пересечения прямой с осью x.Используя уравнение y = 3x — 6, установите y=0, чтобы найти точку пересечения по оси x.
0 = 3x — 6
3x = 6
х = 2
X-пересечение равно 2
Наклон параллельных линий
Если известен наклон линии, любая параллельная ей линия будет иметь такой же наклон, и эти линии никогда не пересекутся.
Наклон перпендикулярных линий
Если известен наклон линии, любая линия, перпендикулярная к ней, будет иметь наклон, равный отрицательной обратной величине известного наклона.
Перпендикулярно означает, что линии при пересечении образуют угол 90°.
Допустим, у вас есть линия с наклоном -4. Каков наклон прямой, перпендикулярной к ней?
- Сначала возьмите отрицательный наклон вашей линии
-(-4) = 4 - Во-вторых, возьмите обратное число.
 4 — целое число, поэтому его знаменатель равен 1. Обратное 4/1 равно 1/4.
4 — целое число, поэтому его знаменатель равен 1. Обратное 4/1 равно 1/4. - Отрицательная инверсия наклона -4 равна наклону 1/4.
- Линия, перпендикулярная исходной линии, имеет наклон 1/4.
Дальнейшее изучение
Брайан Маклоган (2014) Определение наклона между двумя точками в виде дробей, 10 июня. На https://www.youtube.com/watch?v=Hz_eapwVcrM
Использование формулы наклона для определения наклона линии
«Крутизна» линии в плоскости координат xy называется наклоном.Наклон может быть положительным (линия поднимается слева направо), отрицательным (линия падает слева направо), нулевым (прямая линия) или даже неопределенным (вертикальная линия). В этом уроке мы рассмотрим, как рассчитать уклон, используя формулу уклона и две точки вдоль линии.

реклама
Формула наклона
Наклон линии часто называют «подъемом над участком». Это следует из формулы, которая представляет собой изменение y, деленное на изменение x.Другими словами, учитывая две точки, вы найдете разницу между значениями y и разделите на разницу между значениями x.
Примеры
Чтобы понять эту формулу, давайте рассмотрим пару примеров. Во-первых, мы рассмотрим случай, когда вам просто даны две точки на прямой и вас просят найти наклон. Затем мы увидим, как найти наклон, если вместо этого вам просто дан график.
Пример (данные две точки)
Найдите наклон прямой, проходящей через точки \((–1, 5)\) и \((1, 9)\).
Решение
Примените формулу наклона, полагая \((x_1, y_1) = (–1, 5)\) и \((x_2, y_2) = (1, 9)\).
\(\begin{align}\text{slope} &= \dfrac{y_2 – y_1}{x_2 – x_1} \\ &= \dfrac{9 – 5}{1 – (-1)} \\ &= \ dfrac{4}{2} \\ &= \bbox[border: 1px сплошной черный; padding: 2px]{2}\end{align}\)
Следовательно, наклон равен 2.
 Часто наклон обозначается буквой m, поэтому вы также можете написать свой ответ как «\(m = 2\)».
Часто наклон обозначается буквой m, поэтому вы также можете написать свой ответ как «\(m = 2\)».Пример (с использованием графика)
Найдите наклон линии на графике ниже.
Решение
Сначала найдите две точки на прямой. Вы можете выбрать любые две точки, поэтому постарайтесь выбрать точки, с которыми будет легко работать или которые легко считываются с графика.
Теперь выберите одну точку как \((x_1, y_1)\), а другую как \((x_2, y_2)\). Неважно, какие из них какие, если вы согласны со своим выбором в формуле. Здесь мы допустим \((x_1, y_1) = (–2, 6)\) и \((x_2, y_2) = (0, 1)\).
\(\begin{align}\text{slope} = m &= \dfrac{y_2 – y_1}{x_2 – x_1}\\ &= \dfrac{1 – 6}{0 – (-2)}\\ & = \dfrac{-5}{2}\\ &= \bbox[border: 1px сплошной черный; padding: 2px]{-\dfrac{5}{2}}\end{align}\)
Другие возможности
Наклон линии может быть либо неопределенным, либо равным нулю.Это особые случаи, и они более подробно рассматриваются в следующих уроках:
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и наборы задач.

Подпишитесь, чтобы время от времени получать электронные письма (раз в пару или три недели), чтобы узнавать о новинках!
РодственныеУравнения прямых: форма точки-наклона | Пурпурная математика
Пурпурная математика
В предыдущем уроке мы видели форму пересечения наклона для прямых линий.Другой формат уравнений прямой линии называется формой «точка-наклон». Для этого они дают вам точку ( x 1 , y 1 ) и уклон м , и вы подставляете его в эту формулу:
Пусть вас не пугают нижние индексы. Они просто предназначены для того, чтобы указать точку, которую они дают вам. У вас есть общие « x » и общие « y », которые всегда присутствуют в вашем уравнении, а затем у вас есть конкретные x и y из точки, которую они вам дали; конкретные x и y — это то, что указано в формуле.

MathHelp.com
Вот как вы используете формулу угла наклона:
Найдите уравнение прямой, имеющей наклон
м = 4 и проходящей через точку (–1, –6).
Это та же самая строка, которую я нашел на предыдущей странице, поэтому я уже знаю ответ (а именно, y = 4 x – 2). Но давайте посмотрим, как этот процесс работает с формулой точка-наклон.
Мне дали м = 4, х 1 = –1 и у 1 = –6.
. Я подставлю эти значения в форму «точка-наклон» и найду « y =»:
Я подставлю эти значения в форму «точка-наклон» и найду « y =»:г – г 1 = м ( х – х 1 )
г – (–6) = (4)( х – (–1))
у + 6 = 4 ( х + 1)
у + 6 = 4 х + 4
у = 4 х + 4 – 6
у = 4 х – 2
Это соответствует результату, который я получил, подключившись к форме пересечения наклона.Это показывает, что на самом деле не имеет значения, какой метод вы используете (если это не указано в тексте или учителем). Вы можете получить один и тот же ответ в любом случае, поэтому используйте тот метод, который вам удобнее.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске уравнения линии с помощью формулы точка-наклон.
 Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите «Ответить», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите «Ответить», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)(Нажав «Просмотреть шаги» на экране ответов виджета, вы перейдете на сайт Mathway, где вы можете зарегистрироваться для получения бесплатной семидневной пробной версии программного обеспечения.)
Вы можете найти уравнение прямой линии, используя форму точка-наклон, если они просто дадут вам пару баллов:
Найдите уравнение прямой, проходящей через точки (–2, 4) и (1, 2).
Я уже отвечал на этот вопрос, но давайте посмотрим на процесс. Я должен получить тот же результат; а именно:
y = (– 2 / 3 ) x + 8 / 3 ).

Учитывая две точки, я всегда могу найти наклон:
Затем я могу использовать любую точку в качестве моей ( x 1 , y 1 ) вместе с этим наклоном, который я только что вычислил, и подставить эти значения в форму точка-наклон.Используя (–2, 4) как ( x 1 , y 1 ), я получаю:
г – г 1 = м ( х – х 1 )
y – (4) = ( – 2 / 3 )( x – (–2))
y – 4 = ( – 2 / 3 )( х + 2)
y – 4 = ( – 2 / 3 ) x – 4 / 3
y = ( – 2 / 3 ) x – 4 / 3 + 4
y = ( – 2 / 3 ) x – 4 / 3 + 12 / 3
y = ( – 2 / 3 ) x + 8 / 3
Это тот же ответ, который я получил, когда вставил ту же информацию в форму пересечения наклона на предыдущей странице.
 Таким образом, если ваш текст или учитель не указывает метод или формат для использования, вы можете (и должны!) использовать любой формат, который соответствует вашему вкусу, потому что вы получите один и тот же ответ в любом случае.
Таким образом, если ваш текст или учитель не указывает метод или формат для использования, вы можете (и должны!) использовать любой формат, который соответствует вашему вкусу, потому что вы получите один и тот же ответ в любом случае.Вы можете использовать приведенный ниже виджет Mathway, чтобы попрактиковаться в нахождении уравнения линии по двум точкам. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите «Ответить», чтобы сравнить свой ответ с ответом Mathway. (Или пропустить виджет и продолжить урок.)
(Нажав «Просмотреть шаги» на экране ответов виджета, вы перейдете на сайт Mathway, где вы можете зарегистрироваться для получения бесплатной семидневной пробной версии программного обеспечения.)
В рабочих примерах в следующем разделе я буду использовать формулу точка-наклон, потому что так меня учили, и это то, что требуется в большинстве книг.
 Но мой опыт показывает, что многие студенты предпочитают включать наклон и точку в форму линии, пересекающей наклон, и находить b . Если это работает лучше для вас, используйте этот метод вместо этого.
Но мой опыт показывает, что многие студенты предпочитают включать наклон и точку в форму линии, пересекающей наклон, и находить b . Если это работает лучше для вас, используйте этот метод вместо этого.URL-адрес: https://www.Purplemath.com/modules/strtlneq2.htm
Маркер «ласточкин хвост» для уклонов и углов
У меня были некоторые заинтересованные клиенты, которые спрашивали, почему соотношение 1:4 было использовано для оригинального маркера типа «ласточкин хвост». Я должен отметить, что в то время как одна сторона Saddle-Tail предназначена для ласточкиного хвоста, другая сторона представляет собой удобный седловидный квадрат, поэтому на второй стороне вообще нет отношения! Это важная особенность Saddle-Tail, так как это два инструмента в одном, что позволяет вам использовать один инструмент для обеих операций при выполнении соединений типа «ласточкин хвост».

Я работаю по дереву в первую очередь хвостами, поэтому я сначала использую наклонную сторону Saddle-Tail для разметки своих хвостов. После того, как распилили хвосты и вырезали отходы, я использую готовую хвостовую доску, чтобы пометить штифты на конце доски. Для этой операции я использую разметочный нож, чтобы убедиться, что стыки выровнены плотно, без зазоров. Затем я использую квадратную сторону Saddle-Tail, чтобы нанести угловые метки на конец доски, чтобы продлить вертикальную открытую часть штифта вниз по поверхности доски до базовой линии.Я планирую работать с хорошим другом и мастером по дереву онлайн, чтобы сделать короткое видео в следующем месяце или около того, чтобы показать этот процесс. Оставайтесь с нами в этом блоге для его публикации.
Мне очень нравится наклон 1:4 или 14 градусов (это невероятно близко, как вы скоро увидите здесь) для моих ласточкиных хвостов. Другие производители маркеров типа «ласточкин хвост» используют коэффициенты для подмножества своих маркеров и степени для других.
 Например, популярная компания по производству деревообрабатывающих инструментов и каталогов использует наклоны 1:6, 1:8, а затем использует 14 градусов для своего третьего предложения маркеров типа «ласточкин хвост».Я решил, что буду использовать коэффициенты для всех наклонов маркера типа «ласточкин хвост». Я мог бы выбрать все углы, но я выбрал пропорции и придерживался их.
Например, популярная компания по производству деревообрабатывающих инструментов и каталогов использует наклоны 1:6, 1:8, а затем использует 14 градусов для своего третьего предложения маркеров типа «ласточкин хвост».Я решил, что буду использовать коэффициенты для всех наклонов маркера типа «ласточкин хвост». Я мог бы выбрать все углы, но я выбрал пропорции и придерживался их.Чтобы помочь столярам, которые хотели бы знать эквивалентные углы, которые представлены соотношениями и отношениями популярных круглых чисел, вот полезная таблица:
Вы можете видеть, что эти отношения невероятно близки к популярным углам в градусах. Было бы чрезвычайно трудно уловить эти различия в стыках ласточкиного хвоста на предмете мебели на глаз.
Таким образом, при смыкании 1:4 Saddle-Tail для всех практических целей составляет 14 градусов, 1:6 близко к 10 градусам, а 1:8 составляет около 7 градусов. Лучше не слишком беспокоиться об этих небольших различиях в соотношениях и углах и лучше всего сосредоточиться на получении наиболее точных результатов с помощью проектов типа «ласточкин хвост» с точной компоновкой, точным пилением и долблением.



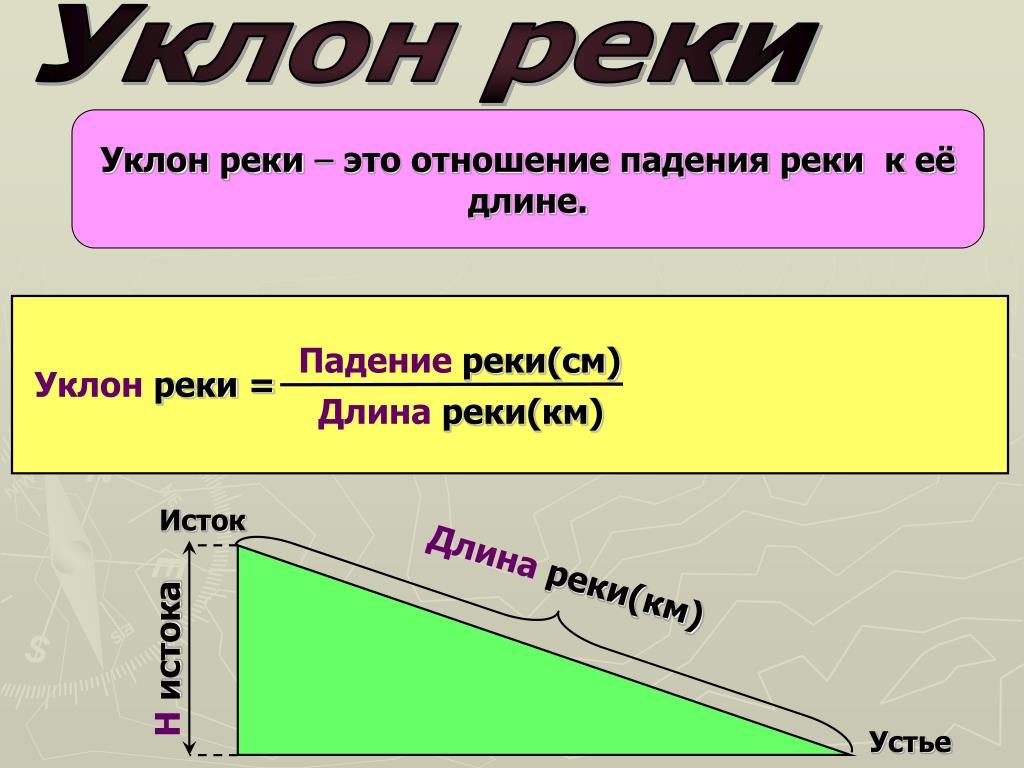
 (Уклон 1%).
(Уклон 1%). 14.1).
14.1). Если вы хотите, вы также можете отправить нам электронное письмо с этим именем или URL-адресом веб-страницы и сообщить нам, что не сработало и какая информация вам нужна.
Если вы хотите, вы также можете отправить нам электронное письмо с этим именем или URL-адресом веб-страницы и сообщить нам, что не сработало и какая информация вам нужна.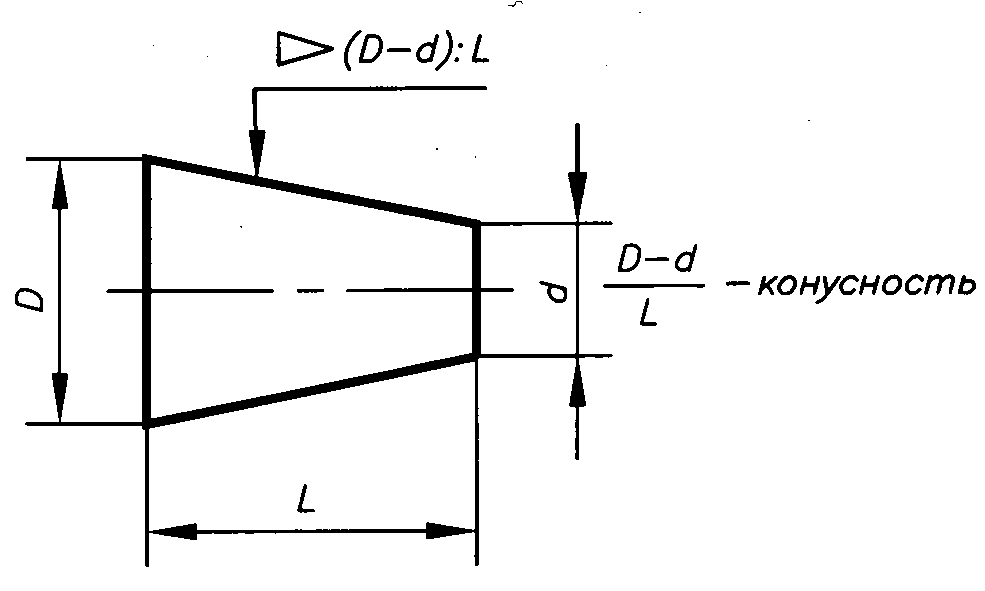 Патроны для веретен кольцепрядильных и крутильных машин. Конус 1:38 и 1:64.
Размеры
Патроны для веретен кольцепрядильных и крутильных машин. Конус 1:38 и 1:64.
Размеры  1
1 Часть 1. Общие требования»
Часть 1. Общие требования»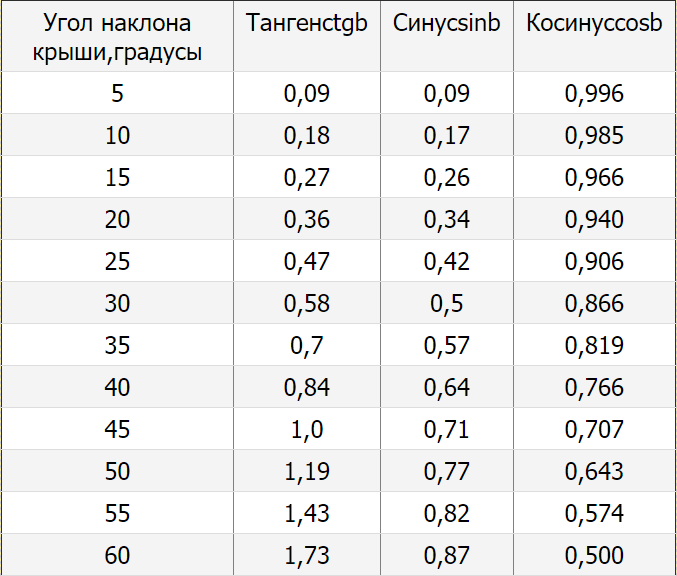 Конусы для крестовой намотки для крашения. Половина угла конуса 4° 20″»
Конусы для крестовой намотки для крашения. Половина угла конуса 4° 20″» Конусы крестовой намотки. Часть 5. Размеры,
допуски и обозначения конусов с половиной угла при вершине 5°57″
Конусы крестовой намотки. Часть 5. Размеры,
допуски и обозначения конусов с половиной угла при вершине 5°57″ Размеры
Размеры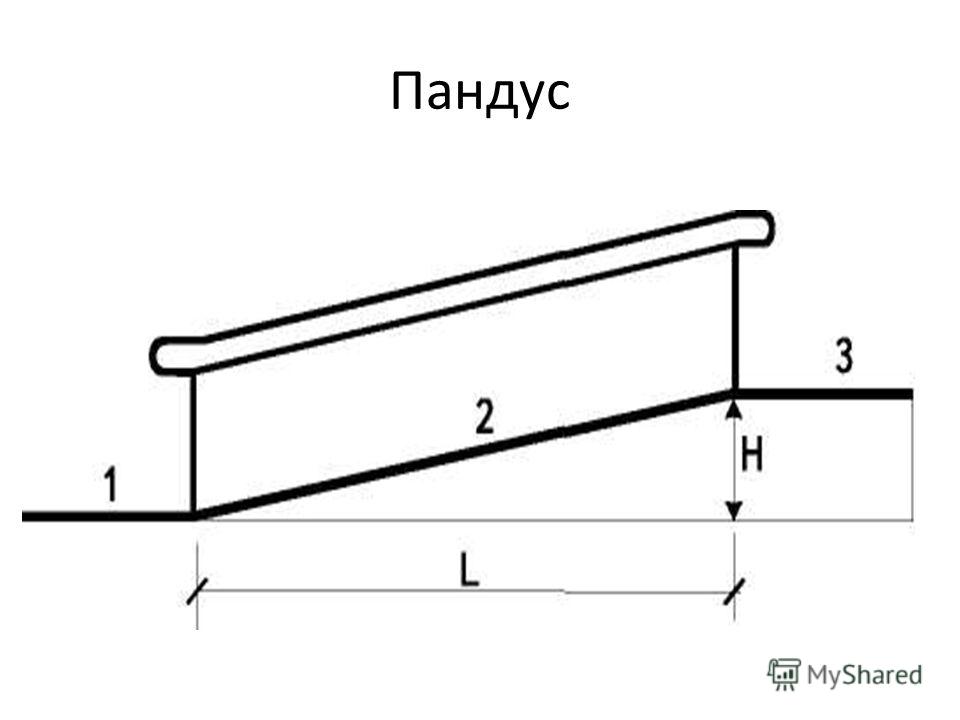 См. приведенное ниже уравнение.
См. приведенное ниже уравнение. 8.2).
8.2).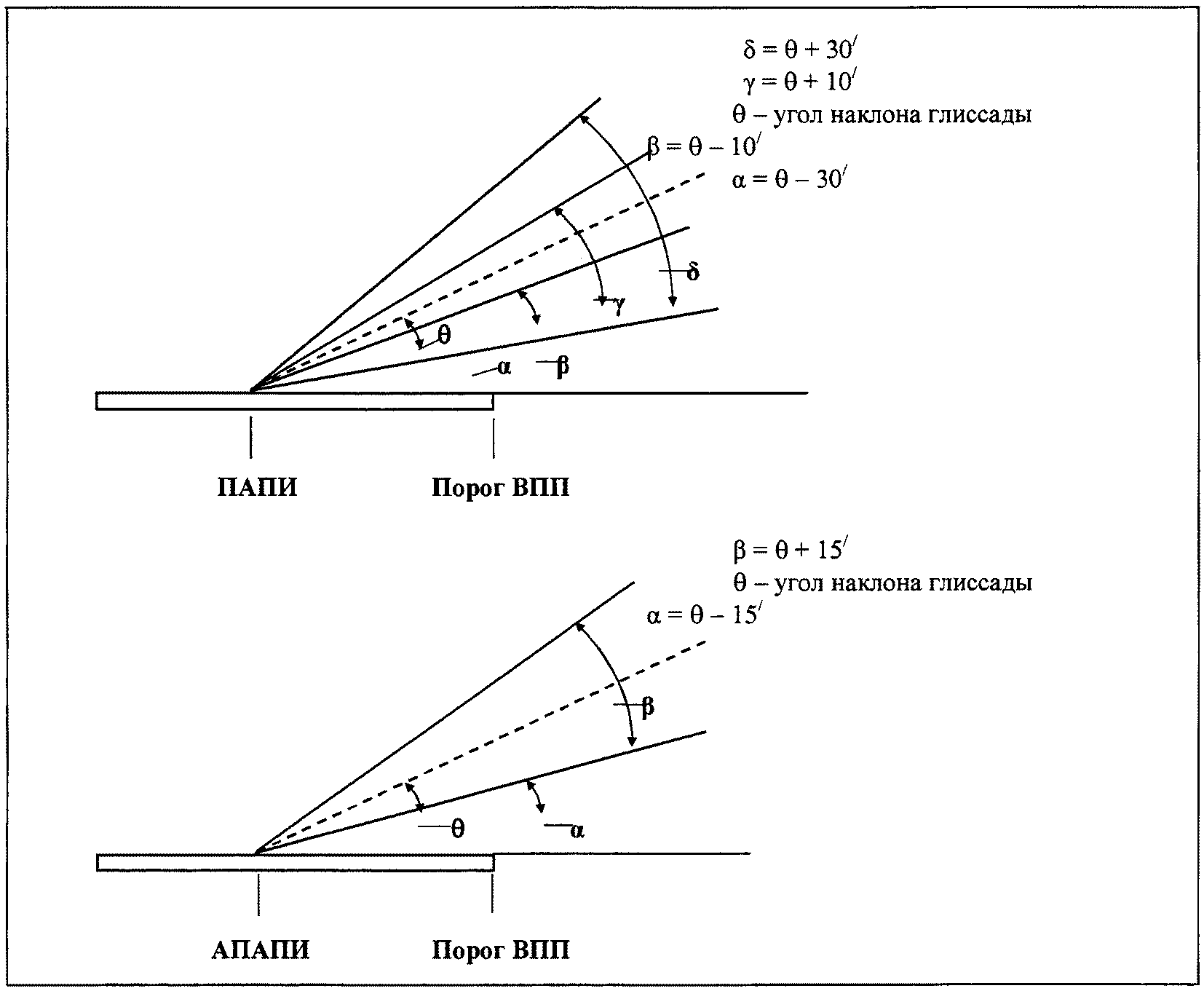 14.1).
14.1).
 Это измерение представляет собой количество дюймов, на которые поднимается крыша за 12 дюймов.
Это измерение представляет собой количество дюймов, на которые поднимается крыша за 12 дюймов.
 Конечно, статья NACHI больше ориентирована на черепицу, а Mule-Hide больше не производит черепицу, но информация о соотношении уклона и уклона так же актуальна и для крыш с малым уклоном.
Конечно, статья NACHI больше ориентирована на черепицу, а Mule-Hide больше не производит черепицу, но информация о соотношении уклона и уклона так же актуальна и для крыш с малым уклоном.
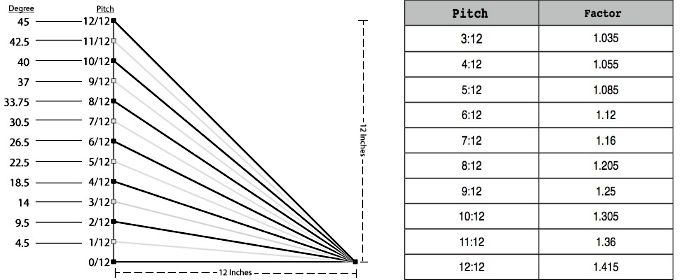 Например, для крыши высотой 4 фута и пролетом 24 фута шаг равен «от 1 до 6», что можно выразить как дробь 1/6. Шаг «от 12 до 24» выражается как 1/2.
Например, для крыши высотой 4 фута и пролетом 24 фута шаг равен «от 1 до 6», что можно выразить как дробь 1/6. Шаг «от 12 до 24» выражается как 1/2.



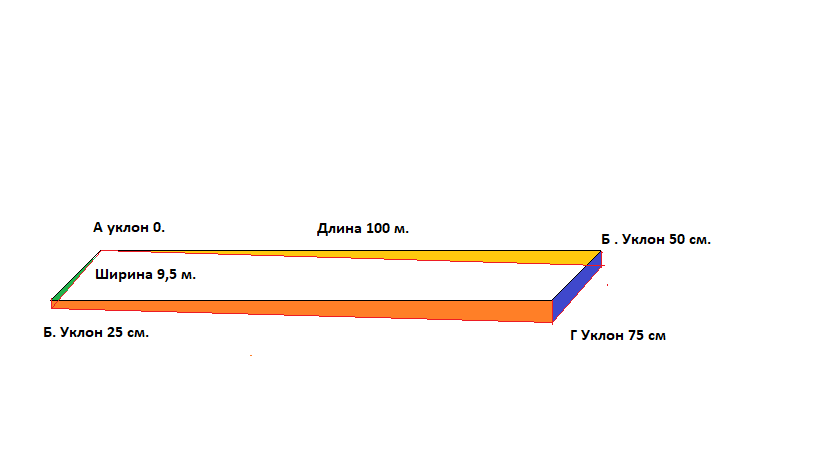
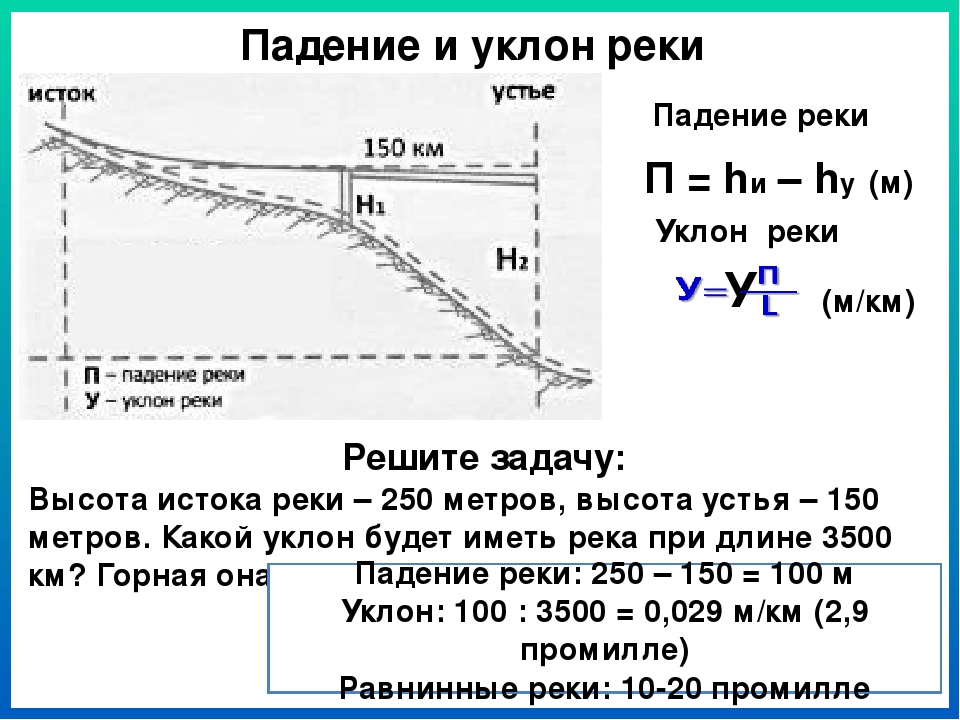 Это точка пересечения прямой с осью x.
Это точка пересечения прямой с осью x.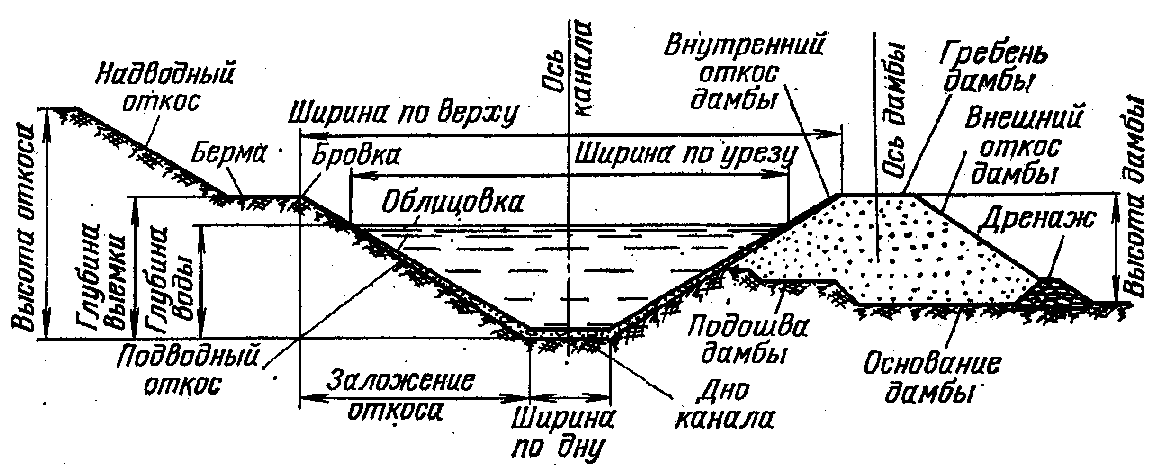 4 — целое число, поэтому его знаменатель равен 1. Обратное 4/1 равно 1/4.
4 — целое число, поэтому его знаменатель равен 1. Обратное 4/1 равно 1/4.
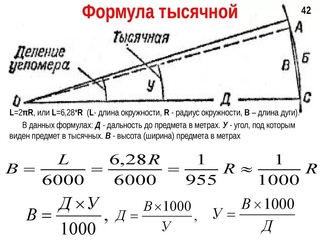 Часто наклон обозначается буквой m, поэтому вы также можете написать свой ответ как «\(m = 2\)».
Часто наклон обозначается буквой m, поэтому вы также можете написать свой ответ как «\(m = 2\)».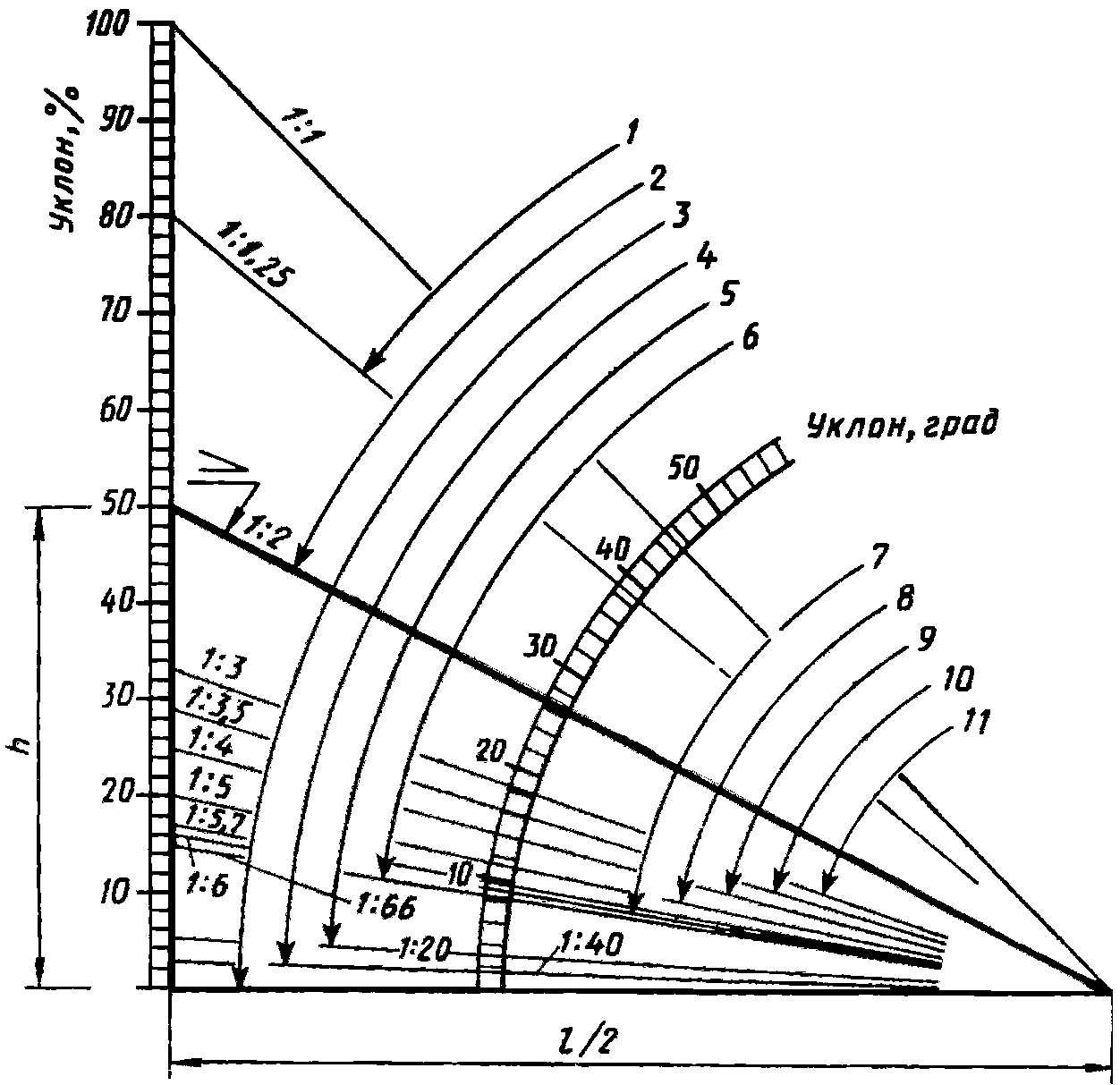
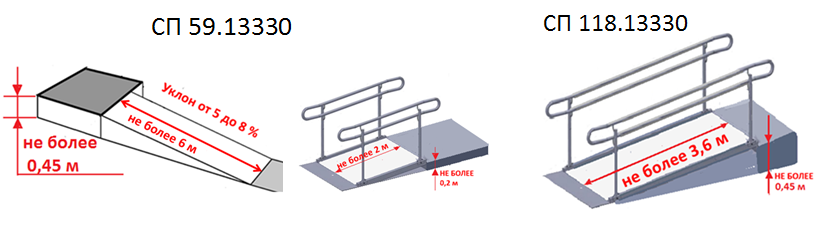
 Я подставлю эти значения в форму «точка-наклон» и найду « y =»:
Я подставлю эти значения в форму «точка-наклон» и найду « y =»: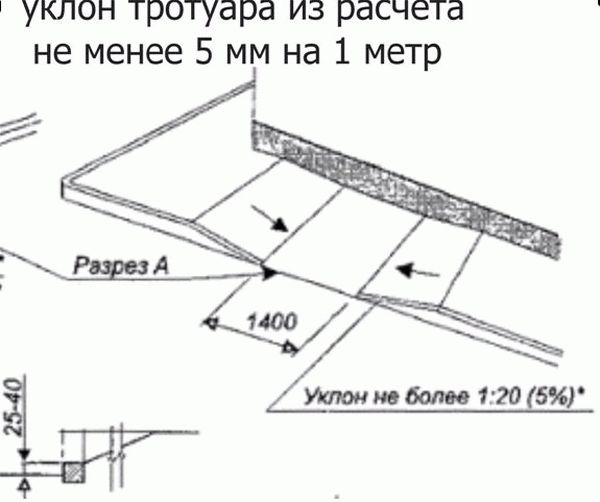 Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите «Ответить», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите «Ответить», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
 Таким образом, если ваш текст или учитель не указывает метод или формат для использования, вы можете (и должны!) использовать любой формат, который соответствует вашему вкусу, потому что вы получите один и тот же ответ в любом случае.
Таким образом, если ваш текст или учитель не указывает метод или формат для использования, вы можете (и должны!) использовать любой формат, который соответствует вашему вкусу, потому что вы получите один и тот же ответ в любом случае. Но мой опыт показывает, что многие студенты предпочитают включать наклон и точку в форму линии, пересекающей наклон, и находить b . Если это работает лучше для вас, используйте этот метод вместо этого.
Но мой опыт показывает, что многие студенты предпочитают включать наклон и точку в форму линии, пересекающей наклон, и находить b . Если это работает лучше для вас, используйте этот метод вместо этого.
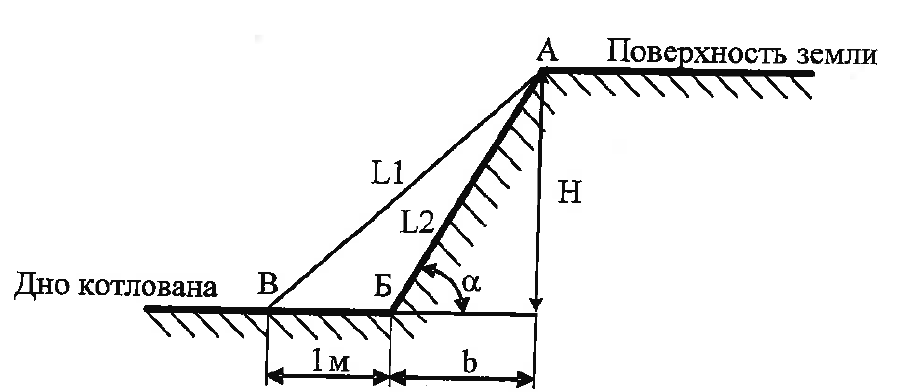 Например, популярная компания по производству деревообрабатывающих инструментов и каталогов использует наклоны 1:6, 1:8, а затем использует 14 градусов для своего третьего предложения маркеров типа «ласточкин хвост».Я решил, что буду использовать коэффициенты для всех наклонов маркера типа «ласточкин хвост». Я мог бы выбрать все углы, но я выбрал пропорции и придерживался их.
Например, популярная компания по производству деревообрабатывающих инструментов и каталогов использует наклоны 1:6, 1:8, а затем использует 14 градусов для своего третьего предложения маркеров типа «ласточкин хвост».Я решил, что буду использовать коэффициенты для всех наклонов маркера типа «ласточкин хвост». Я мог бы выбрать все углы, но я выбрал пропорции и придерживался их.