Как сделать квадратный метр в word?
Современные компьютерные пользователи вовсю эксплуатируют возможности текстового редактора Word. И совершенно правильно делают, ведь данная программа универсальная и очень практичная! С ее помощью можно создавать различные документы, которые будут отличаться по наполнению и оформлению. Секрет заключается в удобном и хорошо продуманном интерфейсе, в бессчетном количестве красивых шрифтов, в разнообразии символов и стилей.
В Ворде можно делать если не все, то почти все, и, если вы читали мои предыдущие статьи, то наверняка уже в этом убедились. Сегодняшний материал я хочу посвятить еще одному вопросу, который интересен многим: как поставить метр квадратный в ворде? Постараюсь ответить на него максимально доступно и развернуто.
Способ первый
Word не был бы таким многофункциональным, если бы не подразумевал несколько сценариев выполнения того или иного действия. Квадратный метр как и значок диаметра, разумеется, встречается не сказать, чтобы часто, но специфика некоторых документов не исключает использование и такого символа.
- Напишите сокращение единицы измерения «метр» – м, а рядом поставьте цифру 2.
- Теперь с помощью мышки выделите двойку и кликните по ней правой мышиной кнопкой.
- В контекстном меню выберите строчку «Шрифт».
- В открывшемся окне отыщите блок «Видоизменение» и поставьте галочку напротив «Надстрочный». Готово, двойка стала чуть выше сокращения «м».
Кстати, есть еще несколько способов, как сделать то же самое. В разделе «Главная» есть блок «Шрифт», в правом нижнем углу которого виднеется маленькая стрелочка. Нажав ее, вы попадете в окно, где также следует выбрать вариант «Надстрочный». Либо можно воспользоваться комбинацией клавиш Ctrl+D, и, вне зависимости от выставленной языковой раскладки, вы опять-таки попадете в то же самое окошко.
Способ второй
Есть еще один способ поставить квадратный метр в документе, и он еще проще предыдущего. Опять-таки, напишите вручную цифру «2», после чего, в блоке «Шрифт» вкладки «Главная», нажмите кнопку с нарисованным символом «x», над которым – маленькая двоечка. Конечно, перед этим стоит выделить нужную цифру мышкой. Таким способом вы напишите «метр квадратный» всего в 2 клика!
Вот такими простенькими способами вы можете пользоваться для того чтобы правильно отобразить в документе Word метр квадратный. Как видите, оба способа чрезвычайно простые, и подойдут любому, даже самому неопытному юзеру.
Видео в помощь
Нередко во время написания текста в Microsoft Word пользователи сталкиваются с необходимости поставить символ или знак, которого нет на клавиатуре. Самое эффективное решение в данном случае — выбор подходящего символа из встроенного набора Ворда, об использовании и работе с которым мы уже писали.
Урок: Вставка символов и специальных знаков в Word
Однако, если вам нужно написать метр в квадрате или метр кубический в Ворде, использование встроенных символов — решение не самое подходящее. Таковым оно не является хотя бы по той причине, что другим способом, о котором мы расскажем ниже, сделать это куда удобнее, да и просто быстрее.
Поставить знак кубического или квадратного метра в Word нам поможет один из инструментов группы
Урок: Как изменить шрифт в Ворде
1. После цифр, обозначающих количество квадратных или кубических метров поставьте пробел и напишите “м2” или “м3”, в зависимости от того, какое обозначение вам нужно добавить — площади или объема.
2. Выделите цифру, идущую сразу после буквы “м”.
3. Во вкладке “Главная” в группе “Шрифт” нажмите на кнопку “Надстрочный знак” (x с цифрой справа вверху).
4. Выделенная вами цифра ( или ) сместится в верхнюю часть строки, став таким образом обозначением квадратных или кубических метров.
Помимо кнопки на панели управления, для включения режима “Надстрочный знак”, который и необходим для написания квадратных или кубических метров, можно также использовать и специальную комбинацию клавиш.
Урок: Горячие клавиши в Word
1. Выделите цифру, идущую сразу за “м”.
2. Нажмите “CTRL” + “SHIFT” + “+”.
3. Обозначение квадратных или кубических метров примет корректный вид. Кликните в месте, после обозначения метров, чтобы отменить выделение и продолжить обычный набор текста.
4. Если необходимо (если после “метров” еще нет текста), отключите режим “Надстрочный знак”.
К слову, точно таким же образом вы можете добавить и обозначение степени в документ, а также подкорректировать обозначение градусов Цельсия. Более подробно об этом вы можете прочесть в наших статьях.
Более подробно об этом вы можете прочесть в наших статьях.
Уроки:
Как в Ворде добавить знак степени
Как поставить градусы Цельсия
Если это необходимо, вы всегда можете изменить размер шрифта символов, расположенных над строкой. Просто выделите этот знак и выберите необходимый размер и/или шрифт. В целом, символ над строкой можно изменять точно так же, как и любой другой текст в документе.
Урок: Как изменить шрифт в Word
Как видите, поставить квадратные и кубические метры в Ворде совсем не сложно. Все, что для этого требуется, нажать одну кнопку на панели управления программы или использовать всего три клавиши на клавиатуре. Теперь вы знаете немного больше о возможностях этой продвинутой программы.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы.
Помогла ли вам эта статья?
Да Нет
СОКРАЩЕНИЯ И СИМВОЛЫ / КонсультантПлюс
Бк │беккерель
В │вольт
Вт │ватт
г │грамм
Гц │герц
ГГц │гигагерц
дтекс │внесистемная единица линейной плотности волокон или
│нитей, равная отношению их массы к длине. 1 дтекс =
│10 мг/м
ИК │инфракрасный
К │кельвин
кВА │киловольт-ампер
квар │киловольт-ампер реактивный
кВт │киловатт
кГц │килогерц
кг │килограмм
кгс │килограмм-сила
км │километр
кН │килоньютон
кПа │килопаскаль
ккал │килокалория
л │литр
м │метр
мас.% │процент содержания по массе
МГц │мегагерц
м- │мета-
м2 │квадратный метр
мг │миллиграмм
мм │миллиметр
мкКи │микрокюри
мН │миллиньютон
Н │ньютон
об.% │процент содержания по объему
о- │орто-
п- │пара-
ПерТ │переменный ток
ПостТ │постоянный ток
с │секунда
сг │сантиграмм
см │сантиметр
см2 │квадратный сантиметр
см3 │кубический сантиметр
сН │сантиньютон
эВ │электрон-вольт
град. С │градус Цельсия
ASTM │Американское Общество испытания материалов
INN │International Nonproprietary Name, Международное
│несобственное название
INNM │International Nonproprietary Name Modified,
│Международное модифицированное несобственное
│название
ISO │International on standardization organization,
│Международная организация по стандартизации
IUPAC │International Union of Pure and Applied Chemistry,
│Международный союз теоретической и прикладной химии
│(ИЮПАК)
% │процент
Примеры
1500 г/м2 │одна тысяча пятьсот грамм на метр квадратный
1000 м/с │одна тысяча метров в секунду
15 град.С│пятнадцать градусов Цельсия
Открыть полный текст документа
Перевод кубических метров в квадратные. Как перевести квадратные метры в кубометры
Переводим квадратные метры в кубометры — формулы и примеры.
Квадратный метр – это единица измерения площади, равная площади квадрата с длиной сторон в 1 метр. Кубический метр – это единица измерения объема, равная объему куба с длиной ребер в 1 метр. Таким образом, эти единицы применяются для измерения различных свойств вещества, поэтому с точки зрения физики говорить о переводе одной единицы измерения в другую не совсем корректно.
Однако на практике часто встречаются ситуации, когда необходимо перевести несхожие единицы измерения (например, квадратный метр в кубический и наоборот).
Перевод квадратных метров в кубические
Чаще всего такая конверсия бывает полезной при расчете количества стройматериалов, так как некоторые из них продаются в метрах кубических, а предназначены для обустройства различных поверхностей, которые удобно измерять в метрах квадратных. Для того чтобы перевести квадратные метры в кубометры, помимо длины и ширины изделия, нужно знать его толщину. Объем изделия вычисляется по формуле V=a*b*c, где
Для того чтобы перевести квадратные метры в кубометры, помимо длины и ширины изделия, нужно знать его толщину. Объем изделия вычисляется по формуле V=a*b*c, где
- a,b и c – длина, ширина и высота в метрах.
Например, нужно обшить комнату вагонкой. Общая площадь стен составляет 200 метров квадратных. Вагонка продается в метрах кубических. Толщина вагонки – 1 см. Для того, чтобы вычислить объем стройматериалов, необходимо произвести следующие вычисления:
- Теперь нужно площадь стен умножить на толщину вагонки в метрах: 200*0,01=2 метра кубических.
Таким образом, для того, чтобы обшить 200 метров квадратных стен понадобится 2 метра кубических вагонки.
Перевод кубических метров в квадратные
В некоторых случаях бывает необходимо перевести кубометры в квадратные метры – то есть измерить, сколько квадратных метров материала содержится в одном кубометре. Для этого нужно знать объем и толщину (высоту) материала и произвести вычисления по формуле: S=V/a, где:
- S – площадь в метрах квадратных;
- V – объем в метрах кубических;
- a – толщина (высота) материала.

Таким образом, если нужно определить, какую площадь можно обшить 1 кубическим метром вагонки толщиной 1 см, нужно:
- Толщину вагонки в сантиметрах перевести в метры: 1/100=0,01 метра;
- Объем вагонки в кубических метрах разделить на полученную толщину в метрах: 1 м3/0,01м=100 м2.
Таким образом, вагонкой, объем которой составляет 1 метр кубический, можно обшить стены площадью 100 метров квадратных.
Для того чтобы эти вычисления не казались такими сложными, достаточно визуализировать понятия кубометра и квадратного метра. Так, чтобы представить себе 1 кубический метр, нужно мысленно нарисовать куб, стороны которого равны 1 метру.
Чтобы представить, сколько квадратных метров содержится в одном кубическом, можно разделить вертикальную плоскость куба на условные полосы, ширина которых равна толщине представляемого материала. Количество таких полос и будет равняться площади материала.
Подсчёт сметы это начальный этап строительства. От его точности зависит то, появятся ли лишние растраты, успеют ли строители закончить проект в срок, хватит ли материалов.
От его точности зависит то, появятся ли лишние растраты, успеют ли строители закончить проект в срок, хватит ли материалов.
Когда речь идёт о кирпичах, рассчитывать смету следует в двух параметрах сколько кирпичей в кладке в кубе и квадрате. Задача усложняется тем, что в учёте учувствуют габариты кирпича, которые различны. Поэтому в первую очередь следует определить, какого размера будет кирпич, применяемый в данном строительстве.
Сколько кирпичей в квадрате кладки
Квадратными метрами измеряется площадь. Для того, чтобы определить сколько кирпичей в 1м2 кладки необходимо произвести простые расчёты:1. Вычислить площадь одного кирпича. Для этого умножить его ширину на длину. Допустим, 250 мм. на 120 мм. = 30 000 кв.мм.
2. Этот результат нужно перевести из квадратных миллиметров в квадратные метры. Для этого нужно поделить его на 1 000 000 (потому что 1кв.м.=1 000 000 кв.мм.). Получается 30 000 кв.мм./1 000 000 = 0,03 кв.м. это площадь одного кирпича.
3. Затем, чтобы узнать, сколько кирпича в м2 кладки, следует разделить этот квадрат на площадь одного кирпича. То есть 1кв.м./0,03 кв.м. = 33,3 кирпича. Рекомендуется округлять в большую сторону 34 кирпича на один квадрат.
То есть 1кв.м./0,03 кв.м. = 33,3 кирпича. Рекомендуется округлять в большую сторону 34 кирпича на один квадрат.
Сколько кирпичей в кубе кладки
Кубическими метрами измеряете объём. Для определения количества кирпича в 1м3 кладки, потребуются результаты вычисления пощади:1. Чтобы узнать объём, требуется умножить длину на высоту и ширину. Так как произведение длины и ширины есть площадь, вычисление которой было рассмотрен выше, то берём этот готовый показатель (то есть 0,03 кв.м) и умножаем его на ширину кирпича в метрах 0,065 м. 0,03кв.м х 0,065м. = 0,00195 куб.м. объём одного кирпича.
2. Вычисляем, сколько кирпича в м3 кладки простым действием 1куб.м./0,00195 куб.м. = 512,8 кирпичей. И округляем снова в большую сторону 513 кирпичей в кубе кладки.
То, сколько кирпичей в кубе кладки может зависеть от раствора, который их соединяет, если речь идёт о более точном подсчёте. Это касается и расчёта площади тоже. В некоторых случаях учитывает показатель толщины этого раствора.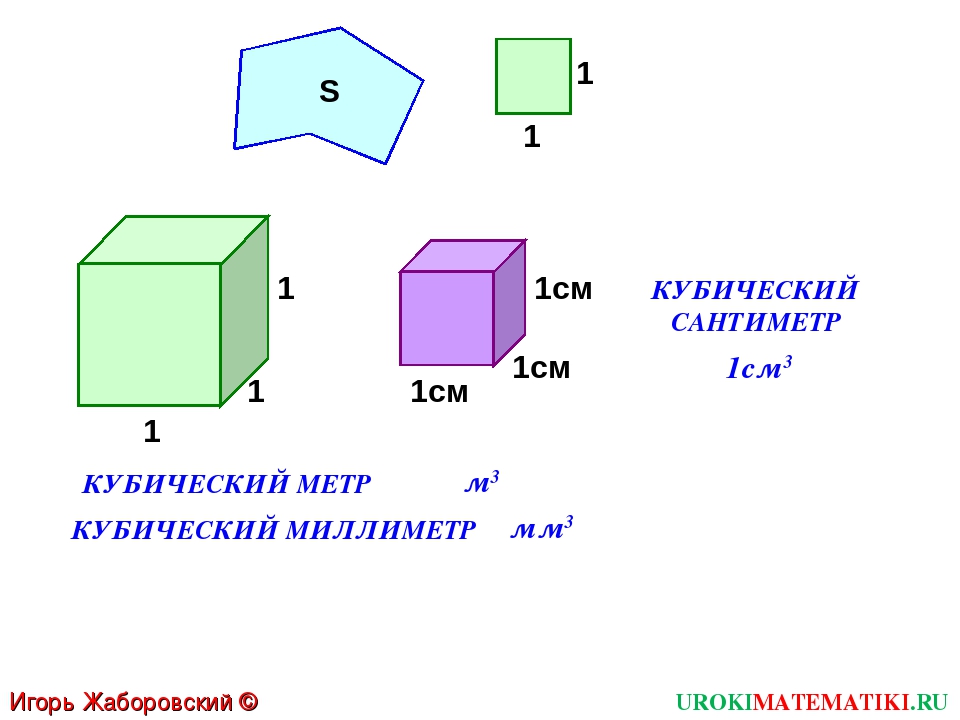 И здесь коэффициент может быть разным, так как это зависит от качества и количества веществ, применяемых в составлении раствора. Но чаще всего можно обойтись и без учёта данного параметра.
И здесь коэффициент может быть разным, так как это зависит от качества и количества веществ, применяемых в составлении раствора. Но чаще всего можно обойтись и без учёта данного параметра.
В данных примерах был взять стандартный кирпич размером 250х120х65 мм. Если в стройке используется другой размер, то результаты, естественно, будут иными.
Сколько квадратных метров доски в кубе: габариты изделий, количество деталей, расчет объема и площади
Разбираться, сколько досок в квадратном метре, сколько кубов материала нужно для реализации того или иного проекта, сколько квадратов можно обшить одним кубометром материала и т.д. должен любой, кто планирует стройку или ремонт. И хоть сегодня несложно найти табличные значения практически для любой ситуации, желательно все же понимать, как осуществляются расчеты, и при необходимости уметь провести вычисления своими руками.
Чтобы понять, сколько здесь материала, придется провести нехитрые расчеты
Габариты досок
Кубометр доски – это сколько? Один из самых распространённых вопросов, которые задают мастера-новички.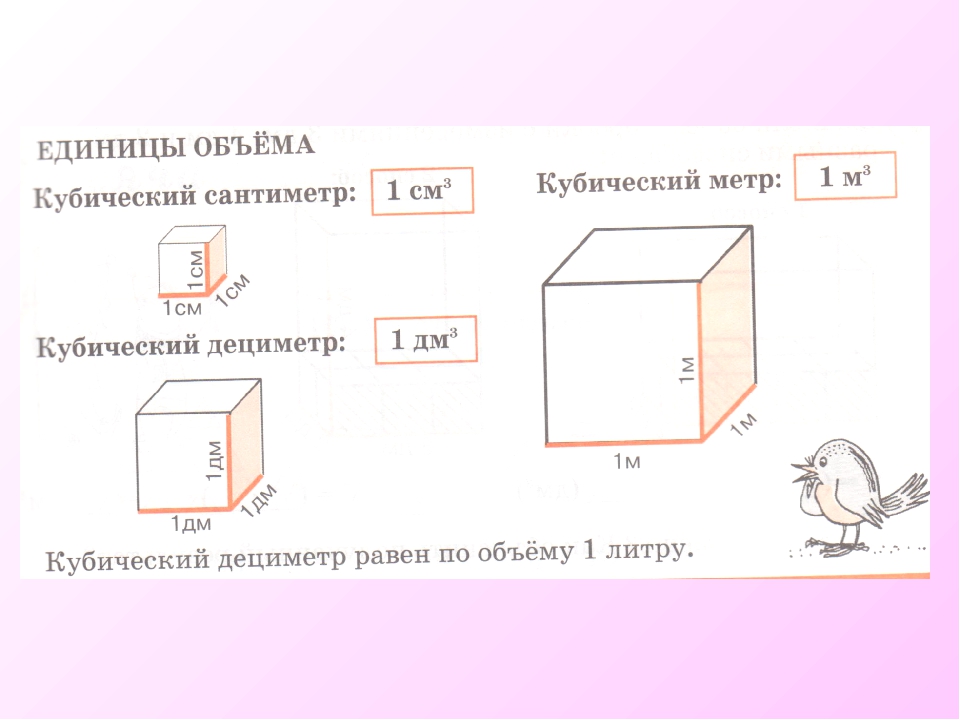 На самом деле на этот вопрос можно дать предельно простой ответ: это, смотря о каком пиломатериале речь!
На самом деле на этот вопрос можно дать предельно простой ответ: это, смотря о каком пиломатериале речь!
Схема определения линейного размера пиломатериала
Как правило, для строительных и ремонтных работ применяют заготовки, произведенные по ГОСТ 8486-86. Этот норматив, регламентирующий основные требования к пиломатериалам хвойных пород (для лиственных есть отдельный документ – ГОСТ 2695-83), определяет, какой размер может иметь изделие.
В принципе, подобрать нужную деталь несложно, но все же есть определенные ограничения, которые и лимитируют производство заготовок:
- толщина – от 16 до 75 мм;
- ширина – от 75 до 275 мм;
- длина – от 1 до 6 м.
Естественно, встречаются и отступления. Так, при необходимости можно заказать изготовление деталей с другим соотношением толщины и ширины. Их цена, конечно, будет выше, чем стандартных, но при необходимости и наличии подходящего сырья можно выпилить практически любую заготовку.
Стандартная длина составляет от 1 до 6 м
Что касается длины, то здесь все несколько сложнее.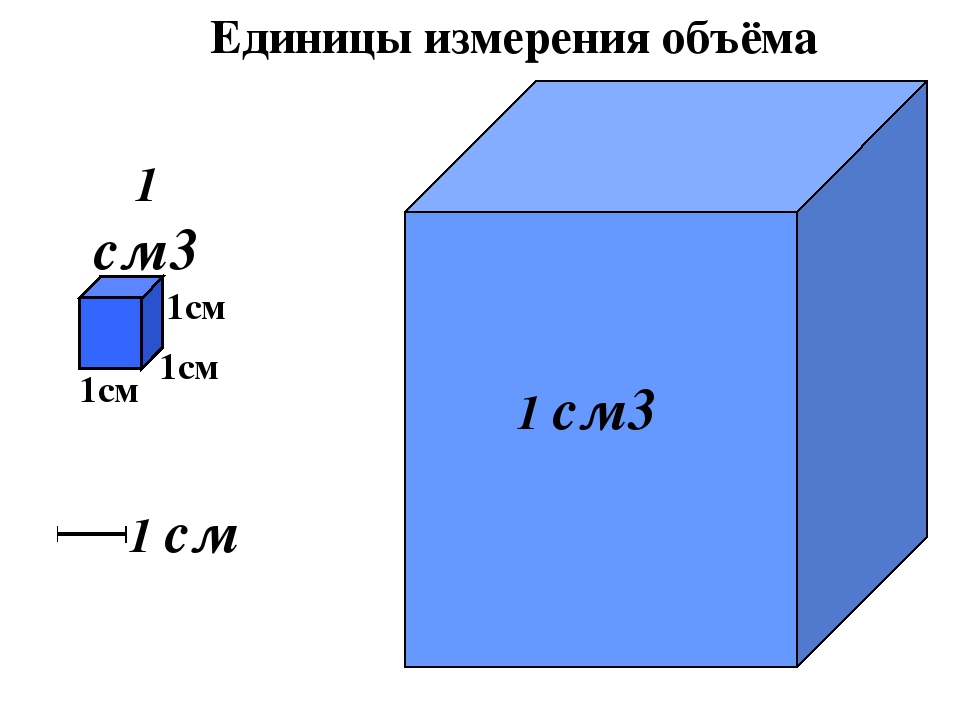 Найти заготовки длиннее 6 м получается далеко не всегда, поскольку эта величина ограничена габаритами товарного вагона. Так что более длинные доски пилятся исключительно под заказ и перевозятся автотранспортом, что удорожает материал.
Найти заготовки длиннее 6 м получается далеко не всегда, поскольку эта величина ограничена габаритами товарного вагона. Так что более длинные доски пилятся исключительно под заказ и перевозятся автотранспортом, что удорожает материал.
В принципе, этой информации будет вполне достаточно, чтобы мы, зная основные параметры изделий, могли рассчитать, сколько 6 метровых досок в кубе, и какую площадь они займут при обшивке либо укладке на пол.
Примеры расчетов
Количество деталей в кубе
Пиломатериалы обычно реализуются по объему
Итак, первую часть этого раздела мы посвятим определению того, сколько досок в кубометре. Задача эта достаточно проста, поскольку нам достаточно 1 м3 поделить на объем одной детали.
Единичный объём вычисляем по формуле Д х Ш х Т, где:
Обратите внимание!
Рассчитывая, сколько досок в одном кубометре, нужно не забывать о переводе единиц, так как обычно параметры поперечного сечения указываются в миллиметрах, а длина – в метрах.
Фото калькулятора, используемого для вычислений
В качестве примера вычислим, сколько в кубе 4 метровых досок шириной 150 мм и толщиной 25 мм:
- Вычисляем объем одной заготовки: 4 х 0,150 х 0,025 = 0,015 м3.
- Определяем количество деталей: 1 / 0,015 = 66,7.
- Округляем до целого значения, получая 66 штук.
Обратите внимание!
Обычно округляют до последней целой цифры.
Это, конечно, несколько противоречит правилам математики, но в данном случае стоит ориентироваться на сложившуюся практику.
Чтобы вам было проще рассчитывать количество досок в кубе – таблица 4 метра / 6 метров приводится ниже:
Естественно, имея под рукой такую таблицу, посчитать, сколько метров доски в кубе (погонных, о квадратных мы поговорим ниже), будет очень легко: берем количество досок и умножаем на их длину.
Так, для деталей 4000х50х100 этот показатель будет равен: 50 х 4 = 200 м. пог.
Еще один вариант таблицы соотношения объема и количества
Объем и площадь
Следующая инструкция посвящена определению площади, которую можно обшить/покрыть, израсходовав одни кубометр пиломатериала.
Чтобы обустроить напольное покрытие, как на этом фото, нужно заранее вычислить объем материала для отделки требуемой площади
- Здесь в первую очередь необходимо определить площадь одного элемента, просто умножив его длину на ширину. Так, если мы планируем обшивать стену деревянной вагонкой 3 м с шириной 220 мм и толщиной 20 мм, то площадь одной доски будет равна 3 х 0,22 = 0,66 м2.
- Затем определяем количество таких изделий в кубометре. Объем одной доски будет равен 3 х 0,22 х 0, 02 = 0,0132 м3. Следовательно, в кубе у нас будет 1 / 0,0132 = 75 деталей заданного размера.
- Далее полученное количество умножаем на площадь одной доски. 75 х 0,66 = 49,5 м2.
Обратите внимание!
Высчитывая, сколько квадратных метров в 1 кубе доски – вагонки, нужно принимать во внимание не фактические размеры панелей, а размеры «видимой части».
Связано это с тем, что при монтаже шипы замковых элементов скрываются в пазах, и ширина уменьшается, так что расхождение теоретического расчета с фактическим может доходить до 8 -10%.
При расчетах с вагонкой длина шипа не учитывается
Также при переводе кубатуры в объем нужно помнить, что иногда возникает необходимость укладки досок без стыков. При этом следует подбирать детали с такой длиной, которая обеспечит появление минимального количества отходов, иначе наши затраты на покупку материала существенно (и неоправданно!) возрастут.
Все рекомендации, приведенные выше, касались работы с обрезной доской, ровным деревянным брусом, вагонкой и т.д. Однако для решения различных задач иногда задействуются необрезная доска и горбыль, которые имеют неправильную форму.
В этом случае для вычисления хотя бы приблизительного объема материала поступаем следующим образом:
Объем необрезной заготовки или горбыля вычислить куда сложнее
- Сначала определяем среднюю толщину заготовки. Для этого выполняем несколько промеров в самой толстой и самой тонкой части, суммируем полученные результаты и делим на количество измерений.
- Затем рассчитываем среднюю ширину по тому же алгоритму.

Обратите внимание!
Чем ближе форма изделия к правильному параллелепипеду, тем меньше промеров нужно сделать для получения сколько-нибудь точного значения.
- Полученные средние величины перемножаем, затем умножаем на длину необрезной планки/горбыля, и получаем объем единицы пиломатериала.
Можно поступить и несколько проще. Зная, что выход полноценной доски из необрезных заготовок составляет около 70 – 80% по объему, мы просто приобретаем сырье с запасом, умножая требуемую величину на коэффициент 1,25 – 1,3. Впрочем, так мы тоже получим только приблизительный результат, потому вероятность избытка/недостатка материала все же будет присутствовать.
Заключение
Мы надеемся, что следуя приведенным советам, вы разберетесь, как посчитать квадратный метр доски, как определить количество деталей в кубометре и т.д. Более подробную информацию можно найти на в этой статье, а если у вас в ходе изучения методик возникнут вопросы, вы сможете задать их в комментариях ниже!
http://rubankom. {3} \right) \]
{3} \right) \]
Сколько вагонки в 1 кубическом метре: расчеты кубических метров
Покупая строительный материал, следует уже знать, сколько его понадобится. Это одно из важнейших правил. Не зря сейчас сложились некоторые нормы продажи пиломатериалов. Ведь не всем под силу произвести расчеты. Не секрет, что изделия, созданные из древесины, в основном не считаются в штуках или по весу. Как правило, для этого берется во внимание специальная таблица, позволяющая узнать, сколько, например, вагонки в квадратном или кубическом метре.
Блок-хаус
Поэтому стоит рассмотреть этот вопрос подробнее.
Количество штук в кубическом метре
Чтобы выполнить расчет, нужно взять во внимание определенные особенности измерения размеров изделий. Тем не менее, кубатура определяется по неизменному принципу. И это не влияет на породу или сорт материала. Если стоит задача вычислить, какое количество вагонки приходится на куб, следует задействовать рабочую поверхность.
Сначала нужно измерить длину, ширину (только полезную) и толщину одной штуки товара. Например, речь идет о вагонке с такими габаритами: 17х140х6000 мм.
Исходя из таких данных, необходимо рассчитать объем планки. Как это сделать? Нужно перевести значения в другую единицу измерения – метры: 0,017х0,14х6 = 0,0142 м3.
Теперь один метр кубический нужно разделить на получившееся значение. Получаем 70,42. Округлять это число нужно в большую сторону – 71 штука.
Количество «квадратов» в кубометре
Для приобретения вагонки может потребоваться произвести расчеты, чтобы узнать, какая площадь материала имеется в кубическом метре. Ведь показатель определяется и толщиной товара.
Сначала нужно измерить толщину вагонки. Если речь идет о древесине, этот показатель может находиться в пределах от 1,2 до 2,5 см. Только нужно перевести данные в метры, ведь объем так же измеряется в этой единице.
Итак, если толщина материала составляет 1,4 см, то получаем значение 0,014 м. На это число нужно разделить кубический метр. Получаем: 1:0,014 см = 71,42 «квадрата».
На это число нужно разделить кубический метр. Получаем: 1:0,014 см = 71,42 «квадрата».
Таким образом, для определения количества материала совсем необязательно знать высшую математику. Достаточно выполнить простейшие расчеты.
Расчет для применения материала внутри помещения
Прежде чем покупать материал, в данном случае вагонку, в обязательном порядке придется производить расчеты для определения точного его количества. Ведь купить нужно не все, что есть в магазине, а определенный объем, который нужен для выполнения поставленной задачи – отделки помещения. Поэтому общую квадратуру стоит разделить на отдельные изделия. Таким образом, рассчитываем плоскость, как простой прямоугольник.
Не помешает и определить длину отрезков, поскольку вагонка может иметь разную длину.
Итак, нужно сначала измерить ширину и длину комнаты. Таким образом, можно определить площадь потолка. Безусловно, в этом есть смысл, если эта плоскость подлежит отделке вагонкой.
После этого следует определить площадь всех стен. Делается это, зная ее длину и высоту умножаем эти значения. Необходимо отметить, что параллельные стены, как правило, имеют одинаковую площадь.
После этого полученные данные нужно суммировать. От этого числа нужно отнять площадь дверных и оконных проемов. Не стоит забывать учесть ниши, кладовки и прочие особенности строения.
Расчет для применения материала снаружи здания
В этом случае расчеты ведутся по такому же принципу. Единственный нюанс: поверхностей будет учитываться намного меньше. И если все делать самостоятельно, то сложности могут возникнуть на этапе определения площади фронтона.
Итак, нужно определить площадь стен, предварительно узнав высоту и длину каждой. То есть процедура аналогична. Чтобы определить площадь фронтонов, следует высоту умножить на длину основания, а затем разделить на два.
После этого полученные цифры нужно суммировать, а затем отнять площадь проемов.
Рекомендация: поскольку установка выполняется по принципу паз-шип, а расчетах следует использовать значение полезной ширины вагонки.
Расчет количества вагонки на примере
- Допустим, мы имеем помещение 3х2 метра и с высотой потолков 2,5. В этом случае целесообразно использовать изделия длиной как раз 2,5 метра.
- Например, будет использоваться вагонка с полезной шириной 10 см. Найдем значения, сколько изделий понадобится для каждой стены:
- 3:0,1 = 30 штук.
- 2:0,1 = 20 штук.
Теперь умножаем полученные значения на 2 и суммируем: 30х2+20х2 = 100 досок. Если в пачке имеется десять изделий, понадобится десять пачек вагонки.
- Вряд ли наша комната не имеет хотя бы одной двери и окна. А эти площади также следует учесть.
Допустим, имеется дверной проем 1х2 метра и окно 2х1 метр. Тогда выполняем расчет:
(1+2):0,1 = 30 штук.
Следовательно, от полученного значения общего количества изделий нужно отнять это значение:
100-30 = 70 изделий. А это значит 7 пачек.
А это значит 7 пачек.
Итоги
Таким образом, произвести необходимые расчеты можно достаточно просто, особенно опираясь на приведенную информацию. Только нельзя не добавить к вышеизложенной информации важную пометку. Ко всем полученным итоговым данным рекомендовано добавлять еще десять процентов про запас. Это обязательное условие, если вы не хотите в процессе монтажа бежать в магазин за партией материала, аналогичного купленному, которого, кстати, может не оказаться в наличии.
Смотрите также:
Периметр, площадь и объем — Помощник для школьников Спринт-Олимпик.ру
Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:
Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
К примеру, если сказано, что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. К примеру, если сказано, что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из граней, ребер и вершин. На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грани параллелепипеда, чёрным цветом — рёбра, красным — вершины.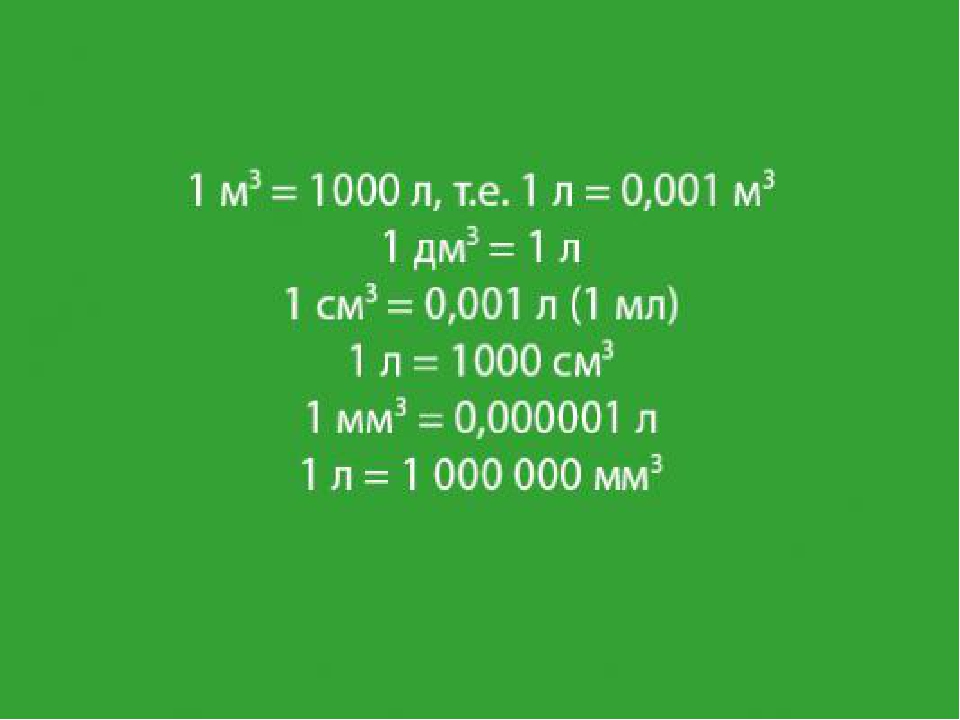
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.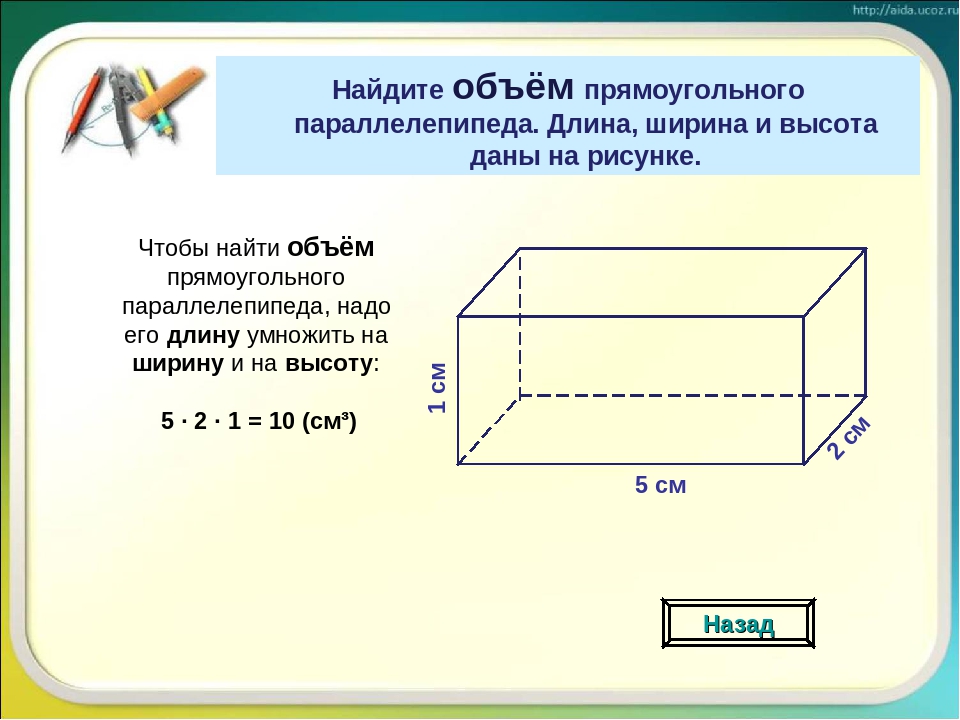
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.
Длина, ширина и высота одного кубического метра равны 10 дм
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру.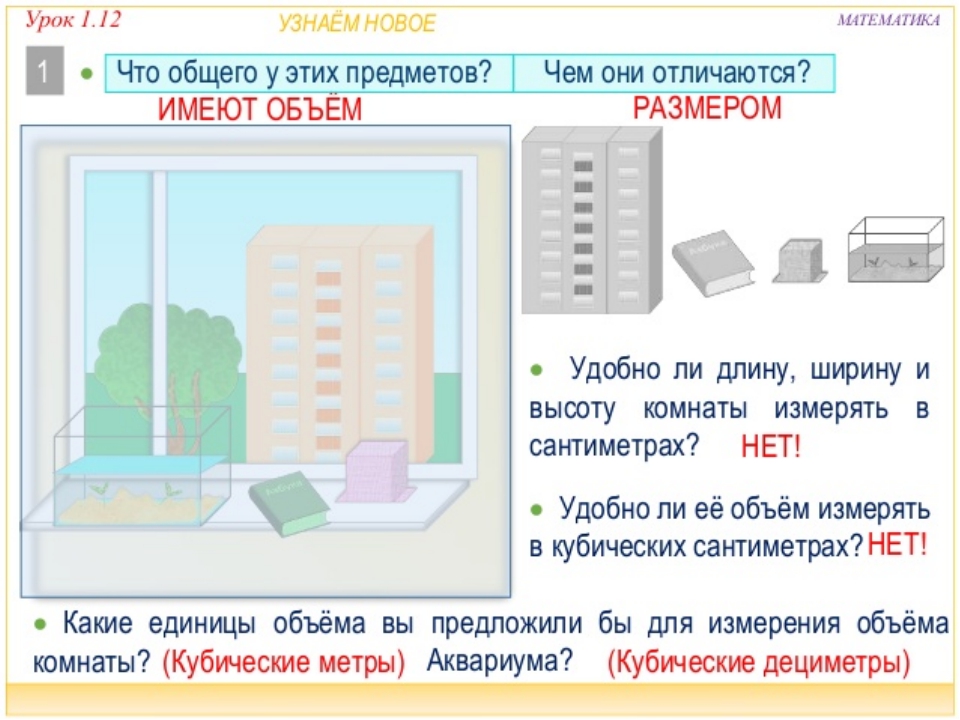 А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет
длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.Решение
a — длина
b — ширина
c — высота
a = 42 м
b =
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Предыдущая
Математика с нуляСтепень с целым показателем
СледующаяМатематика с нуляОдночлены
За отопление — по квадратным метрам!
Разрешите поделиться собственным мнением на статью «Квадратный метр стал гигакалорией?», опубликованной 26.05.2015г.
Считаю, конкретного ответа, почему квадратные метры превратились в Гкал и кубические метры, специалист так и не дал.
Формулы по начислению за тепловую энергию на отопление не изменились, так же как не изменились и Постановления Правительства РФ по начислению за горячее водоснабжение. В Постановлениях Правительства РФ от 14.02.2015 №129 и от 06 мая 2011 №354 с изменениями четко установлен порядок перевода двухкомпонентного тарифа в однокомпонентный и определение платы за горячее водоснабжение в рублях за кубический метр.
Однако ведомства дают незаконные распоряжения предъявлять за горячую воду в Гкал, тем самым лоббируя интересы энергетиков и их необоснованные начисления. Вот и сейчас для того, чтобы скрыть от потребителей понятную для всех оплату за отопление по квадратным метрам по стоимости 1 кв. метра, снова одну и ту же формулу по начислению за отопление трактуют так, как выгодно монополисту.
Плата за отопление рассчитывается по формуле:
P = Si * N * T, где :
Si — площадь квартиры жилого помещения собственника в кв. м;
N — норматив потребления коммунальной услуги по отоплению на 1кв.метр жилой площади в Гкал;
Т — тариф на тепловую энергию на 1 Гкал.
И весь вопрос в том, как определить норматив потребления тепловой энергии на 1 квадратный метр. В Минусинске многоквартирные дома оснащены общедомовыми коллективными приборами учета (ОДПУ). И вот от того, как правильно определят норматив потребления тепловой энергии на 1 кв. метр по показаниям прибора учета (ОДПУ), и зависит, правильно ли будет начислена оплата за отопление в отопительный период в соответствии с Постановлением № 354.
N — норматив потребления на 1 кв. метр при наличии ОДПУ рассчитывается как частное от деления:
V d — объем потребленной тепловой энергии по ОДПУ
S об. — общая площадь дома
Этот норматив потребления на 1 кв. м (в Гкал) умножается на тариф на тепловую энергию за 1 Гкал и получается тариф на отопление (в рублях) на 1 кв. метр жилой и нежилой площади.
Именно на этот тариф и должны умножить площадь квартиры жилого помещения собственника! И ему все будет понятно. Чиновники же, такое впечатление, стараются наоборот: чем непонятнее для собственника, тем выгоднее для монополиста и недобросовестных компаний и ТСЖ.
Вопросы еще остаются. Как правильно будет определяться тепловая энергия, потребленная конкретным домом? Как правильно будет предъявлена оплата со стороны ресурсоснабжающей организации, которая не производит перерасчет на фактическую температуру холодной воды, тем самым завышая при предъявлении оплату за отопление? А если учесть, что при утверждении тарифа на 1 Гкал РЭК Красноярского края завысил его почти вдвое, то оплата за отопление и горячее водоснабжение должна значительно уменьшиться.
Кому, как не чиновникам городской власти, нужно бы защищать интересы жителей Минусинска?
Т. ПУРГИНА
Материал опубликован в выпуске «Власть Труда» №47 (18.059) от 18 июня, 2015
Как вы переводите кубические метры в квадратные метры? — AnswersToAll
Как вы переводите кубические метры в квадратные метры?
Квадратный метр обозначает площадь и равен произведению длины и ширины / ширины. Кубический метр обозначает объем и равен произведению длины, ширины / ширины и высоты. Следовательно, один квадратный метр равен одному кубическому метру, разделенному на высоту.
Сколько квадратных метров в одном кубическом метре?
Следовательно, чтобы перевести кубический метр в квадратный, нам нужно разделить объем на толщину.Один кубический метр равен одному квадратному метру…. Кубический метр в квадратный метр.
| Кубический метр (м3) | Квадратный метр (m2) |
|---|---|
| 1 | 1 |
| 2 | 1,5874 |
| 3 | 2,0801 |
| 4 | 2,5198 |
Как перевести кубики в квадрат?
Квадратный фут = кубический фут ÷ глубина. Итак: 5 ÷ 0,25 = 20. У нас есть общая сумма: 20 квадратных футов.
Сколько площади покрывает кубический метр?
С мульчей 1 кубический метр покрывает примерно 13 м2 при толщине 70 мм. Допустим, у вас есть 27 м2 площади и вы хотите, чтобы она была покрыта с рекомендуемым покрытием 70 мм, вам нужно будет приобрести 2 кубических метра.
Сколько квадратных метров в 100 кубических метрах?
Последние преобразования квадратных метров в Кубические метры
| КВАДРАТНЫЕ МЕТРЫ | КУБИЧЕСКИХ МЕТРОВ | |
|---|---|---|
| 100 м2 | = | 100 м3 |
| 57 м2 | = | 57 м3 |
| 90 кв.м | = | 90 м3 |
| 71 м2 | = | 71 м3 |
Что означает 1 кубический метр?
: единица объема, равная кубу длиной один метр с каждой стороны: стере.
Какая формула кубометра?
Формула кубического метра для измерения различных единиц Метр = l × b × h = кубический метр. Сантиметр = l × b × h ÷ 10,00 000 = кубические метры.
Как рассчитать кубический метр?
Формула расчета куб. Метра
- Длина (в метрах) X Ширина (в метрах) X Высота (в метрах) = Кубический метр (м3)
- Мы можем определять размеры в метрах, сантиметрах, дюймах, футах.
Сколько тонн гравия в кубическом метре?
Кубический метр обычного гравия весит 1680 кг 1.68 тонн.
Как рассчитать кв.м?
Умножьте длину и ширину. После того, как оба измерения будут преобразованы в метры, умножьте их вместе, чтобы получить измерение площади в квадратных метрах.
Сколько тонн в кубическом метре?
1,5 тонны
При просмотре продукта в Интернете, например декоративной гальки, почвы или песка, вы заметите несколько цифр, которые могут выглядеть примерно так: 1,5 тонны = 1 кубический метр. Это преобразование объемной плотности.
Как написать 1 кубометр?
Обозначение кубических метров — м3. Менее формально кубический метр иногда сокращенно называют кубометром. При расчете объема важно понимать, что объем пропорционален кубу линейного измерения.
Какие примеры кубических единиц?
Некоторыми примерами кубических единиц в метрических единицах являются кубические метры, кубические сантиметры, а в обычных единицах измерения — кубические дюймы, кубические футы. Забавные факты. Все 6 граней кубической единицы квадратные, и все ее 12 ребер имеют длину по одной единице каждая.
Какая формула для объема?
Принимая во внимание, что основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.
Что означает кубический метр?
м³
| Кубический метр | |
|---|---|
| Система единиц | SI |
| Шт. Из | том |
| Символ | м³ или | ㎥
Как рассчитать кубические метры в тонны?
Количество кубометров 0.3 на 2,41 (до 2 знаков после запятой).
Перевести кубический метр в квадратный
- Home
- Перевести кубический метр в квадратный
Тип фильтра: За все время Последние 24 часа Прошлая неделя Прошлый месяц
Результаты листинга Преобразовать кубический метр в квадратный
Как преобразовать кубические метры в квадратные метры Quora
9 часов назад Quora.com Другие результаты
Нет прямого преобразования .Уменьшая количество измерений, все, что вы можете сделать, это выбрать проекцию или секцию объекта с большим количеством размеров, и количество возможных способов сделать это бесконечно. Типичная реальная проблема этого
Веб-сайт: https://www.quora.com/How-can-I-convert-cubic-meters-to-square-meters
Категория : Бесплатный конвертерПоказать больше
Конвертер квадратных метров в кубические метры из M2 в кубические метры…
6 часов назад Buildingclub.info Больше результатов
Площадь в квадратных метров (м 2) нужно умножить на толщину в метров . В результате получился объем кубометров (м 3). 1 м 3 = 1 м 2 * 1 м. Квадратный метр калькулятор (м на м2) Квадратный метр от до линейного метров — квадратный метр на погонный метр. Свяжитесь с нами: [адрес электронной почты защищен] Мы используем изображения с сайта Pixabay.com.
Веб-сайт: https://buildingclub.info/calculator/m2-to-m3/
Категория : Бесплатный конвертерПоказать больше
Как преобразовать квадратные метры в кубические метры? -…
4 часа назад Цвета-нью-йорк.com Больше результатов
квадратных метров составляет примерно 10,7 квадратных футов, поэтому 100 квадратных метров составляют примерно 10700 квадратных футов. Площадь 10 x 10 метров = 100 м² = 1076,391 фут² = или площадь около 32,8 x 32,8 фута. С уважением, Джеймс. 100 на 1 метров или 10 на 10 метров или любого промежуточного размера, где…
Веб-сайт: https://colors-newyork.com/how-do-i-convert-square-meters-to -кубические метры /
Категория : Бесплатный преобразователь Показать больше
Как преобразовать квадратные метры в кубические метры…
9 часов назад англ.kakprosto.ru Еще результаты
Чтобы перевести квадратных метров в кубов , нужно знать толщину или высоту тех объектов или участков, для которых пересчитывается сумма. Обычно такой перевод — это оплата некоторых строительных материалов, помещений и судов. кубических метров используются для измерения или расчета объема, квадратных метров — для представления площади.
Рейтинг : 4.1 / 5 (56)Расчетное время чтения: 2 минуты
Веб-сайт: https: // eng.kakprosto.ru/how-87065-how-to-convert-square-meters-to-cubic-meters
Категория : Бесплатный преобразовательПоказать больше
Преобразовать метр в квадратный метр, M в M2
7 часов назад Mainfacts.com Другие результаты
Преобразование квадратных метров в квадратных метров , м в м2. Единицы измерения длины, расстояния и площади конвертер , калькулятор, онлайн инструмент. Преобразование табл. Описание, объяснение, формула.
Веб-сайт: https://mainfacts.com/convert-m-to-m2
Категория : Бесплатный конвертерПоказать больше
Конвертировать метр в кубический метр, M в M3
7 часов назад Mainfacts.com Другие результаты
Преобразование метров в кубических метров , м3 в м3. Длина и расстояние, единицы объема и вместимости конвертер , калькулятор, инструмент онлайн. Преобразование табл. Описание, пояснение
Веб-сайт: https: // mainfacts.com / convert-m-to-m3
Категория : Бесплатный конвертерПоказать больше
Онлайн-конвертер единиц ConvertTop
6 часов назад Converttop.com Другие результаты
кубических метров в час: 3600 м³ / ч: кубических метров в минуту: 60 м³ / мин: кубических метров ярдов в час: 4708.60780593 ярдов³ / ч: кубических метров ярдов в минуту: 78,4769753655 ярдов³ / мин: кубических метров ярдов в секунду: 1,30795954836 ярдов³ / с
Веб-сайт: http: // www.converttop.com/
Категория : Бесплатный конвертерПоказать больше
M³ Cubic Meter. Таблица преобразования / Вместимость и…
2 часа назад Convert-me.com Другие результаты
Действительно. 1. Это таблица преобразования для кубических метров ( метрических ). Чтобы переключить устройство, просто найдите на странице тот, который вам нужен, и щелкните его. Также можно перейти на страницу универсальной конверсии . 2. Введите значение, которое вы хотите пересчитать конвертировать ( кубических метров ).Затем нажмите кнопку Convert Me. Ваше значение мгновенно конвертируется во все остальные единицы на странице.
Веб-сайт: https://www.convert-me.com/en/convert/volume/m3.html
Категория : Бесплатный конвертерПоказать больше
Кубические метры в галлоны США (жидкость) Преобразование
9 часов назад Metric-conversions.org Другие результаты
Кубические метры . Метрическая единица объема , обычно используемая для выражения концентрации химического вещества в объеме воздуха.Один кубических метров равен 35,3 кубических футов или 1,3 кубических ярдов. Один кубических метров также равен 1000 литров или одному миллиону кубических сантиметров. Кубических метров в галлонах США (жидкость ) формула
Веб-сайт: https://www.metric-conversions.org/volume/cubic-meters-to-us-liquid-gallons.htm
Категория : Бесплатный конвертерПоказать больше
Калькулятор кубических метров (см, M, футы, дюймы)
6 часов назад Thecalculatorsite.com Другие результаты
кубический метр (или метр, по английскому правописанию) — это единица измерения объема. Чтобы рассчитать вместимость объекта или пространства кубических , вам необходимо измерить ряд размеров, в частности ширину, длину и высоту, а затем выразить их в формуле.
Расчетное время чтения: 1 мин.
Веб-сайт: https://www.thecalculatorsite.com/misc/cubic-meters-calculator.php
Категория : Бесплатный конвертерПоказать больше
9000 Кубометр Метр Куб Объем
6 часов назад Бьюс.com Больше результатов
Кубический метр до Квадратный метр . Как известно, кубических метров — это единица объема, тогда как квадратных метров — это единица площади. Мы получаем кубических метров , когда мы умножаем длину на ширину на толщину и квадратных метров на умножение длины на ширину. Следовательно, чтобы преобразовать кубический метр в квадратный метр , нам нужно разделить объем на толщину.
Расчетное время чтения: 3 минуты
Веб-сайт: https: // byjus.com / maths / cubic-meter /
Категория : Бесплатный конвертерПоказать больше
Калькулятор кубических метров (дюймы, футы, ярды, мм, см, м в кубический метр)
1 час назад Ginifab.com Другие результаты
Блок преобразование и калькуляторы. 1 ярд = 91,44 сантиметра = 0,9144 метра ( преобразовать ярдов в метр ) 1 фут = 30,48 сантиметра = 0,3048 метра ( преобразовать футов в метр ) 1 дюйм = 2.54 сантиметра = 0,0254 метра ( преобразовать дюймов в см) 1 метр = 100 сантиметров ( преобразовать метр в см) 1 миллиметр = 0,1 сантиметра = 0,001 метра ( преобразовать мм в см) Кубический формула счетчика для различных единиц
Веб-сайт: https://www.ginifab.com/feeds/cbm/cubic_meter_calculator.html
Категория : бесплатный конвертерПоказать больше
Конвертировать кубические метры Преобразование объема
8 часов назад Checkyourmath.com Другие результаты
Кубический метр от до Кубический метр футов Преобразование Пример Задача: Преобразование 50 кубических метров в кубических метров футов (показать работу) Формула: м 3 ÷ 0,0283168466 = фут 3 Расчет: 50 м 3 3 Результат: 50 м 3 равно 1,765,73333558 футов 3. Преобразование Таблица. Для быстрого ознакомления ниже приведена таблица преобразования , которую можно использовать для преобразования из м 3 в фут 3.
Веб-сайт: https: // www.checkyourmath.com/convert/volume/cubic_volume/m_feet.php
Категория : Бесплатный конвертерПоказать больше
Преобразование объема газа
9 часов назад Checalc.com Дополнительные результаты
Объем газа Преобразование Преобразование объема газа из заданных условий в кубические футы в минуту (стандартный кубических футов в минуту при 14,7 фунтов на квадратный дюйм, 60 ° F), ACFM (фактические кубических футов на Минута), MMSCFD (миллион стандартных кубических футов футов в день @ 14.7 фунтов на квадратный дюйм, 60 ° F), Нм³ / ч (нормальный кубический метр в час при 1 атм, 0 ° C), см³ / ч (стандартный кубический метр в час при 1 атм, 15 ° C), ACMH ( Фактический кубический метр в час) и ACMS (Фактический кубический метр
Веб-сайт: https://checalc.com/solved/volconv.html
Категория : бесплатный конвертер Показать больше
Калькулятор преобразования 1 квадратный метр в кубический футТолько сейчас Flightpedia.org Больше результатов
1,45 Квадратные метры от до Квадратные сантиметров. 1170000 квадратных метров от до квадратных километров. От 153619 до квадратных метров от до SquareFeet (исследование США), от 2 акров до квадратных метров, миль. 348,75 квадратных метров от до SquareFeet (исследование в США) 348,75 квадратных метров от до SquareFeet (США и Великобритания) от 11200 SquareFeet (США и Великобритания) до квадратных метров . 4
Акров в Га. 2587
квадратных метров соток.Веб-сайт: https://www.flightpedia.org/convert/1-square-meters-to-cubic-feet.html
Категория : Бесплатный конвертерПоказать больше
Кубический метр в кубический Микрометр (м3 до µ) Объем…
Только сейчас Converterin.com Другие результаты
КУБИЧЕСКИЙ СЧЕТЧИК ДО КУБИЧЕСКИЙ МИКРОМЕТР (м3 ДО µ) ФОРМУЛА. Чтобы преобразовать из кубического метра в кубический метр и кубического микрометра, вам необходимо сделать следующее: Сначала разделите 1/1.0e-18 = 999999999999999872 .. Затем умножьте количество кубических метров , чтобы преобразовать в кубических …
Веб-сайт: https://converterin.com/volume/cubic-meter-m3-to -cubic-micrometer.html
Категория : Бесплатный конвертерПоказать больше
Конвертер из MM в M Калькулятор из миллиметров в метры
7 часов назад Squareyards.com Другие результаты
Пример преобразования мм в метры -.Вы хотите преобразовать 10 миллиметров в метры. Чтобы получить ответ, разделите 10 на 1000. 10 ÷ 1000 = 0,1 метра. Это просто. Вам просто нужно записать в голове формулу из миллиметров в метры, и это -. Миллиметры ÷ 1000 = Метр. Миллиметры в Метры Преобразование Таблица.
Веб-сайт: https://www.squareyards.com/blog/mm-to-m-cnvart
Категория : Бесплатный конвертерПоказать больше
Конвертировать кубические километры в кубические метры (км³ → м³ )
6 часов назад Convertlive.com Другие результаты
Преобразование из кубических километров в кубических метров . Введите сумму, которую вы хотите преобразовать в , и нажмите кнопку Преобразовать . Входит в категорию. Объем. К другим единицам. Преобразование табл. Для вашего сайта. км³ Куб. километров в Бушель (Великобритания) буш. бушель (Великобритания) на кубических километров км³.
Веб-сайт: https://convertlive.com/u/convert/cubic-kilometer/to/cubic-meters
Категория : Бесплатный конвертерПоказать больше
Конвертация кубических метров в литры
8 часов назад Метрическая система преобразований.org Другие результаты
Кубические метры . Метрическая единица объема , обычно используемая для выражения концентрации химического вещества в объеме воздуха. Один кубических метров равен 35,3 кубических футов или 1,3 кубических ярдов. Один кубических метров также равен 1000 литров или одному миллиону кубических сантиметров. Кубических метров в литрах по формуле
Веб-сайт: https://www.metric-conversions.org/volume/cubic-meters-to-liters.htm
Категория : Бесплатный конвертерПоказать больше
КАК ПРЕОБРАЗОВАТЬ КВАДРАТНЫЙ МЕТР В КВАДРАТНУЮ НОГУ…
3 часа назад Youtube.com Больше результатов
Квадрат от метров до Квадрат миллиметров // Квадрат метров до Квадрат сантиметров // Квадрат Метр до Квадрат дюймов // Квадрат метров до Квадрат футов // Квадрат метров до квадрата
Веб-сайт: https: // www.youtube.com/watch?v=Zg2VWP0aAEk
Категория : Бесплатный конвертер
Как преобразовать кубический метр в кубические футы, квадрат…
3 часа назад Youtube.com Другие результаты
Как преобразовать кубический метр в кубический футов, квадратный метр от до квадратных футов, квадратных ярдов до квадратных футов смотрите видео Civil Engineeraapko ye video pasand aaye h toh
Website: https: // www.youtube.com/watch?v=Dith81l7yJU
Категория : Бесплатный конвертерПоказать больше
Кубический микрометр в кубический метр (мкМ3) Объем…
Just Now Converterin.com Другие результаты
CUBIC MICROMETER TO CUBIC METER (μ TO m3) FORMULA. Чтобы преобразовать между кубическим микрометром и кубическим метром , вы должны сделать следующее: Сначала разделите 1.0e-18/1 = 0 .. Затем умножьте количество кубических микрометров, которое вы хотите преобразовать в Кубический метр , используйте приведенную ниже таблицу.
Веб-сайт: https://converterin.com/volume/cubic-micrometer-to-cubic-meter-m3.html
Категория : Бесплатный конвертерПоказать больше
Калькулятор кубических метров Калькулятор на 3 дюйма
5 часов назад Inchcalculator.com Дополнительные результаты
кубических метров или кубических метров в британском английском — это мера объема куба, длина, ширина и высота которого равны метрам.Чтобы рассчитать объем кубических метров в , начните с измерения вашего пространства. При измерении найдите длину, ширину и высоту помещения в метров . Затем умножьте три измерения вместе, чтобы найти объем
Расчетное время чтения: 1 мин
Веб-сайт: https://www.inchcalculator.com/cubic-meters-calculator/
Категория : Бесплатный конвертерПоказать больше
Как рассчитать кубические метры 5 шагов
7 часов назад Образование.onehowto.com Другие результаты
Таким образом, если 1 кубических метров равно 35,3 кубических футов, сколько кубических метров будет, например, 67 кубических футов? Умножьте 35,5 на 1 и разделите на кубических метров футов: 35,3 x 1 = 35,3, 67 ÷ 35,3 = 1,89 квадратных футов. Вычислите кубических метров из кубических ярдов. Опять же, в преобразовать кубических ярдов в кубических метров …
Рейтинг : 4.2/5 (13)1 . Первое, что вам нужно сделать для расчета кубических метров, — это определить высоту и ширину, чтобы рассчитать площадь, необходимую для хранения того, что вы хотите. Например, предположим, что у вас есть контейнер шириной 5 метров и длиной 2 метра.
2 . Чтобы найти поверхность, вам нужно умножить ширину и длину, чтобы, следуя примеру, площадь поверхности составляла 5 метров на 2 метра, что равнялось 10 квадратным метрам.
3 . Для расчета кубометров поверхности площадью 10 квадратных метров (5 метров на 2 метра, при высоте 5 метров.Объем работ будет равен следующему: Объем = 5 метров в высоту x 10 квадратных метров = 50 кубических метров
4 . Если вы хотите работать с определенным объемом, вам нужно разделить количество кубических метров на высоту и длину (в данном случае 10). Например, если вы работаете с объемом 30 квадратных метров и хотите хранить его в пространстве шириной 5 метров и длиной 2 метра, разделите 30 кубических метров на 10, чтобы получить ответ 3 метра в высоту.
Веб-сайт: https: // education.onehowto.com/article/how-to-calculate-cubic-meters-373.html
Категория : Ps ConverterПоказать больше
Преобразование кубических метров в кубические мили Преобразование
9 часов назад Convertunits.com Дополнительные результаты
кубических метров или кубических миль Производной единицей объема в системе СИ является кубических метров . 1 кубических метров равно 2,39756488E-10 кубических миль. Обратите внимание, что могут возникать ошибки округления, поэтому всегда проверяйте результаты.Используйте эту страницу, чтобы узнать, как преобразовать из кубических метров в кубических миль. Введите свои собственные числа в форму, чтобы преобразовать единиц!
Веб-сайт: https://www.convertunits.com/from/cubic+meter/to/cubic+mile
Категория : Бесплатный конвертер Показать больше
Конвертировать кубические мили в кубические метры Объем…
9 часов назад Checkyourmath.com Дополнительные результаты
кубических миль — это единица объема как в обычных единицах США, так и в британской системе мер.Обозначение для кубических миль — 3 мили. В кубических метрах 0,0000000002 кубических миль. Что такое кубических метров (м 3)? кубический метр — это единица объема в метрической системе . Обозначение для кубических метров — м 3. Всего 4 168 181 825.44058 кубических метров в
Веб-сайт: https://www.checkyourmath.com/convert/volume/cubic_volume/miles_m.php
Категория
: Бесплатный конвертерПоказать ещеПреобразовать кубический сантиметр / квадратный метр в кубический…
8 часов назад Convertunits.com Подробнее
›› Подробнее с блока преобразователь . Сколько кубических сантиметров / квадратный метр в 1 кубических сантиметрах / квадратных дюймах? Ответ: 1550.0031000062. Обратите внимание, что могут возникать ошибки округления, поэтому всегда проверяйте результаты. Используйте эту страницу, чтобы узнать, как преобразовать из кубических сантиметров / квадратный метр в кубических сантиметров / квадратных метров и кубических сантиметров / квадратных сантиметров / квадратных дюймов.
Веб-сайт: https: // www.3] в регистр тонны [тонна рег] преобразование таблица и преобразование шагов также перечислены. Кроме того, изучите инструменты для преобразования кубических метров или тонны в другие единицы объема или узнайте больше о преобразованиях объема .
Веб-сайт: https://www.unitconverters.net/volume/cubic-meter-to-ton-register.htm
Категория : Бесплатный конвертерПоказать больше
Что такое 25 кубических метров в Кубический фут? Преобразование 25 M3…
5 часов назад Whatisconvert.com Другие результаты
Коэффициент преобразования из кубических метров в кубических метров футов составляет 35,314666572208. Чтобы узнать, сколько кубических метров в кубических футов, умножьте на коэффициент преобразования или используйте преобразователь объема выше. Двадцать пять кубических метров эквивалентны восьмистам восьмидесяти двум целым восьмью шести семи кубическим метрам футов.
Веб-сайт: https: // whatisconvert.com / 25 кубических метров в кубических футах
Категория : Бесплатный преобразователь Показать больше
Вычислить линейные метры в кубические метры и затраты…
4 часа назад Blocklayer.com Другие результаты
Кубические и линейные измерения — это две разные вещи, так как же преобразовать одно в другое? Cubic Метры измеряют объем. Линейные метры измеряют длину. Если ваш материал имеет заданную ширину и толщину, вы можете рассчитать объем данной общей длины этого материала.
Веб-сайт: https://www.blocklayer.com/linear-cubic.aspx
Категория : Бесплатный конвертерПоказать больше
Конвертировать граммы на кубический метр в фунты на кубический…
6 часов назад Convert-to.com Дополнительные результаты
Этот онлайн-инструмент для одностороннего преобразования конвертирует единицы плотности из граммов на кубических метров (г / м3) в фунты на кубических футов (фунт / ft3) мгновенно онлайн.1 грамм на кубических метров (г / м3) = 0,000062 фунта на кубических футов (фунт / фут3). Сколько фунтов на кубических футов (фунт / фут3) в 1 грамме на кубических метров …
Веб-сайт: http://convert-to.com/conversion/de density/convert-g-per-m3 -to-lb-per-ft3.html
Категория : Бесплатный преобразователь Показать больше
Преобразование кубических метров в галлон (м³ в галлоны)
2 часа назад Конверсия-метрическая.org Другие результаты
Это очень простой в использовании преобразователь кубических метров в галлон . Прежде всего, просто введите значение кубических метров (м³) в текстовое поле формы преобразования , чтобы начать преобразование м³ в галлон, затем выберите десятичное значение и, наконец, нажмите кнопку преобразовать , если автоматический расчет не сработал. Значение в галлонах будет автоматически конвертироваться по мере ввода. Десятичное значение — это количество цифр, которое необходимо вычислить.
Веб-сайт : https: // www.convert-metric.org/volume/cubic_meter-to-gallon
Категория : бесплатный конвертерПоказать больше
3500 кубических футов в кубические метры Преобразование Преобразование…
5 часов назад Theunitconverter.com Другие результаты
Кубический футов = длина X ширина X высота. Не существует общепринятого символа, но используется множество сокращений, таких как фут3, фут3, фут / -3 и т. Д. CCF составляет 100 кубических футов. кубических метров : кубических метров (также пишется « кубических метров », символ: м3) — производная единица объема в системе СИ.Он определяется как объем куба с ребрами длиной метров метров.
Веб-сайт: https://www.theunitconverter.com/cubic-foot-to-cubic-meter-conversion/3500-cubic-foot-to-cubic-meter.html
Категория : Бесплатный конвертерПоказать больше
Что такое 2400 кубических метров в литрах? Преобразование 2400 м3…
3 часа назад Whatisconvert.com Другие результаты
Коэффициент преобразования из кубических метров в литры равен 1000.Чтобы узнать, сколько кубических метров в литрах, умножьте на коэффициент преобразования или используйте преобразователь объема выше. Две тысячи четыреста кубических метров эквивалентны двум миллионам четыремстам тысячам литров. Определение кубического метра . кубических метров (также написано « кубических метров
Веб-сайт: https://whatisconvert.com/2400-cubic-meters-in-liters
Категория : Бесплатный конвертерПоказать больше
Тип фильтра: За все время Последние 24 часа Прошлая неделя Прошлый месяц
Пожалуйста, оставьте свои комментарии здесь:
Часто задаваемые вопросы
Сколько метров в квадратном метре?
Квадрат — это число (корневое число), умноженное на себя.Умноженный на метр метр равняется квадратному метру, поэтому 3 метра x 3 метра = 9 квадратных метров .
Как перевести килограммы в квадратные метры?
Один килограмм на квадратный сантиметр равен 10 000 килограмм на квадратный метр, поэтому используйте эту простую формулу для преобразования: килограммы на квадратный метр = килограммов на квадратный сантиметр × 10 000 .
Как перевести кубические метры в дюймы?
Чтобы преобразовать кубический метр в кубический дюйм, умножьте объем на коэффициент преобразования .Один кубический метр равен 61 023,744095 кубических дюймов, поэтому используйте эту простую формулу для преобразования: кубические дюймы = кубические метры × 61 023,744095.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.АВТОР}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.3 в квадратных футах означает: нахождение площади куба в квадратных футах со стороной 1 м. 1 кубический метр — это объем куба со стороной 1м. Количество кирпичей в 100 кубических футах кирпичной кладки. 20 кубических футов в кубические метры = 0,5663: 900 кубических футов в кубические метры = 25,4852: 30 кубических футов в кубические метры = 0,8495: 1,000 кубических футов в кубические метры = 28,3168: 40 кубических футов в кубические метры = 1,1327: 10 000 кубических футов в кубические Метры = 283,1685: 50 кубических футов в кубические метры = 1,4158: 100 000 кубических футов в кубические метры = 2831.3 = 35,31. Кирпичей на квадратный фут Таким образом, если 1 кубический метр равен 35,3 кубическим футам, сколько кубических метров будет, например, 67 кубических футов? ›› Определение: кубический метр. Итак, в 100 кубических футах будет 1350 кирпичей. Один кубический метр равен 35,3 кубическим футам. Чтобы преобразовать кубические метры в кубические футы, заполните поле кубических метров; Формула преобразования. кубические метры в кубические футы. Если его глубина составляет одну десятую метра (10 см), его объем составляет 78,4 кубических метра. Если вы имеете в виду 28 квадратных метров (например, бассейн размером 4 на 7 метров), то объем глубиной в одну десятую метра равен 2.8 м.куб. Кубический метр или стереоскоп — это объем, занимаемый кубом размером 1 м на 1 м на 1 м или эквивалентным физическим пространством любой формы. Давайте будем честными — иногда лучший калькулятор квадратных футов в кубические футы — это тот, который прост в использовании и не требует, чтобы мы даже знали, что такое формула квадратных футов в кубические футы в первую очередь! 1 м * 1 м * 1 м. Это означает, что 3500 рупий / м3 = 99,1 рупий за кубический фут. Но если вы хотите узнать точную формулу для расчета квадратных футов в кубические футы, пожалуйста, проверьте поле «Формула» выше.Ярды) в другой тип единиц (например, легко конвертировать кубический метр (м³) в кубические футы (фут³) с помощью этого бесплатного онлайн-калькулятора единиц измерения. Добавьте кубический метр в тысячу квадратных футов (панели 3/8 дюйма). он понадобится в будущем. 353,14667 Кубических футов (округлено до 8 цифр) Отображение результата как. Как вы знаете, в 1 кубическом футе 13,5 кирпича. Это размер куба со стороной 1 фут. 1 кубический метр (м3) равно 35,3146667 кубических футов (фут3). Как рассчитать кубические футы с квадратными футами? Эта функция впервые появилась в Excel 2007, поэтому… Чтобы преобразовать кубические метры в кубические футы, умножьте значение кубического метра на 35.3146667. Кубические футы. 1 грамм на кубический метр (г / м3) = 0,000062 фунта на кубический фут (фунт / фут3). Умножьте 35,5 на 1 и разделите на размер в кубических футах: 35,3 x 1 = 35,3, 67 ÷ 35,3 = 1,89 квадратных футов. Описание функции. Мы можем найти 35,314 квадратных футов на метр, либо посмотрев на таблицу, например здесь, либо вычислив вручную: 3,2808 футов на метр. Вопрос должен быть от кубических метров до кубических футов. Это размер куба со стороной 1 метр. КУБИЧЕСКИЙ МЕТР НА ДОПОЛНИТЕЛЬНУЮ НОГУ (м3 ДО ac) ФОРМУЛА.Чтобы преобразовать кубический метр в акро-фут, вам необходимо сделать следующее: Сначала разделите 1 / 0,028316847 * 43560 = 0,00081071. Кубические метры могут быть сокращены до м³, а также иногда сокращены до кубических метров, кубических метров, кубических метров или MTQ. Это ровно 1000 литров. В этом случае 1 x 35,314 = 35,314 кубических футов. Это размер куба со стороной 1 метр. 28-метровый квадрат равен 28 умноженным на 28 метров или 784 квадратных метра. В метрических единицах кубический фут — это куб со сторонами 0,3048 метра. Это ровно 1000 литров.Например, если ширина измеряемой области составляет 10 футов 5 дюймов, вы разделите 5 на 12 и получите 0,42. Перевести кубические метры в кубические футы. м и мощность 0,15 м, тогда площадь 1 / 0,15 = 6,67 м 2. Пример 2: 1 куб. Расчет объемов бетонных плит, стен, нижних колонтитулов, колонн, ступеней, бордюров и водостоков. Вычислить кубические метры в кубических ярдах. Кубическое измерение — это трехмерная производная линейной меры, поэтому кубический фут определяется как объем куба со сторонами 1 фут в длину.1 кубический метр: объем, образованный кубом, каждая сторона которого имеет один метр. Метров). Сколько квадратных футов равно одному квадратному метру? 1 MMCF = 28316,846592 м 3. Чтобы преобразовать кубические футы в кубические метры, умножьте значение в кубических футах на 0,0283168466 или разделите на 35,3146667. Функция Excel CONVERT преобразует число из одного типа единиц (например, кубический фут (пл кубических футов) — это единица измерения объема, используемая теми странами, которые признают имперскую систему и обычную систему США (США, Великобритания, ряд стран Африканского и Тихоокеанского регионов и др.один метр = 3,281 фута. Попробуйте сделать это в системе СИ. Например, 1 кубический метр можно записать как 1 м³, 1 куб. М, 1 куб. М, 1 куб. М или 1 MTQ. Re: кубический метр в квадратный метр Дорогие друзья! Предположим, у вас есть 1 кубический метр, чтобы преобразовать его в квадратные метры, у вас должна быть толщина в метрах .. она зависит от толщины Пример 1: 1 куб. Кубический метр или кубический метр — это единица объема. квадратных футов единицы измерения уровня и кубических метров на единицу измерения объема двух по сравнению с Робом Гельфманом.Этот онлайн-инструмент одностороннего преобразования мгновенно конвертирует единицы плотности из граммов на кубический метр (г / м3) в фунты на кубический фут (фунт / фут3). mts. Разделите общую стоимость на количество квадратов… Следовательно, вы должны применить правило трех. 1 миллион кубических футов равен 28316,846592 кубических метров (базовая единица СИ). Например, чтобы вычислить, сколько кубических футов составляет 10 кубических метров воды, умножьте 10 на 35,3146667, и получится 353,146667 фут3 на 10 м3 воды. 1 м 3 = 35,3146 футов 3. Чтобы найти соответствующий квадратный метр в кубических футах, введите значение в поле перед кнопкой кубический метр и нажмите кнопку кубических футов.Расчет объема квадратной плиты с помощью калькулятора. Затем умножьте количество кубических метров, которое вы хотите преобразовать в акр-фут, используйте приведенную ниже таблицу, чтобы помочь вам. Как мы знаем, объем можно рассчитать, используя площадь и высоту, умножив оба значения, чтобы найти кубические метры, просто умножьте квадратные футы на высоту в футах. Приблизительно 10,76364864 квадратных футов равны одному квадратному метру, поскольку фут определяется как 0,3048 метра в соответствии с международным договором, подписанным в 1959 году, а квадратный фут в квадратном метре тогда просто равен 0.3048 в квадрате. Это определение в соответствии с Международной системой единиц (СИ) и стандартами ISO на величины и единицы [1] [2]. Поскольку преобразование в квадратные метры настолько простое, отменить его просто. Я уверен, вы знаете, что футовая доска — это длина в дюймах, умноженная на ширину в дюймах, умноженную на толщину в дюймах; затем вы берете произведение и делите его на 144, чтобы получить единицы досок. Кубический метр или кубический метр — это единица объема. Кубический фут — это единица объема. Миллион кубических футов.1000 квадратных футов: 1000 квадратных футов (панели 1/2 дюйма) 1000 квадратных футов: 1000 квадратных футов (панели 1/4 дюйма) 1000 квадратных футов: 1000 квадратных футов (панели 1/8 дюйма) 1000 кв. футов Один кубический фут эквивалентен приблизительно 0,02831685 кубических метров или 28,3169 литров. кубический метр в кубические футы Таблица преобразования: кубический метр в кубические футы: кубический метр в кубический фут. Сколько фунтов на кубический фут (фунт / фут3) содержится в 1 грамме на кубический метр (1 г / м3)? Один метр равен 3.281 фут. Отсюда мы получаем следующую формулу для преобразования кубических футов в кубические футы. Кубический фут — это единица объема. Итак, чтобы преобразовать, вам нужно умножить кубические метры на 35,314, чтобы получить кубические футы. Воспользуйтесь нашим калькулятором кубических метров, чтобы рассчитать объем помещения. 3,2808 футов x 3,2808 футов x 3,2808 футов = 35,314 кубических футов. Это размер куба со стороной 1 фут. Дело в том, что дощатый фут — это единица измерения, которая является кубической единицей; в данном случае кубические дюймы. Пример. Рассчитайте кубические футы для площади 4 метра и 8 квадратных футов.Добавьте 0,64 и 12,85, чтобы получить количество кирпичей в 1 кубическом футе, вы получите 0,64 + 12,85 = 13,492 кирпича или, можно сказать, 13,5 кирпича. Кубический метр или кубический метр — это производная единица измерения объема в системе СИ в метрической системе. Например, чтобы вычислить, сколько кубических метров составляет 100 кубических футов воды, умножьте 100 на 0,0283168466, что даст 2,83168466 м3 — 100 кубических футов воды. Загрузите нашу мощную программную утилиту Volume — Lumber Unit Converter, которая поможет вам легко преобразовать более 2100 различных единиц измерения в… Введите размеры вашей бетонной конструкции в американских (дюймах или футах) или метрических единицах (сантиметрах или метрах), чтобы получить объем бетона, который вам понадобится для изготовления этой конструкции, в кубических ярдах.{3}}, но вы хотите знать, сколько места занимает ваша комната. Вы можете использовать калькулятор кубических метров для работы между единицами СИ (международная система), также называемыми метрическими единицами, и традиционными футами и дюймами в британской системе мер. Калькулятор кубических метров в квадратные футы Присоединяйтесь к Yahoo Answers и получите 100 баллов сегодня. 1000 квадратных футов (панели 1/8 дюйма) 1 = 1,6951040026315: 1000 квадратных футов (панели 1/4 дюйма) 1 = 1,1300693350876: 1000 квадратных футов (панели 3/8 дюйма) 1: кубический метр = 0,84755200131573: 1000 квадратных футов футов (1/2 дюйма панели) 1 = 0.56503466754382: 1000 квадратных футов (3/4 дюйма панели) 1 кубический фут (фут3) равен 0,0283168466 кубического метра (м3). 1350 кирпичей рассчитать кубические метры из кубических ярдов, как рассчитать кубические метры на 35,314, чтобы получить футы !, например, 67 кубических футов с квадратными футами) Отобразите результат как 35,314, чтобы получить кубическое преобразование !, если 1 кубический метр фут в кубический футов 4-метрового квадратного … Калькулятор преобразования кубических футов (3/8-дюймовых панелей) — вы, вероятно, получите … кубические футы, площадь 8 квадратных футов, чтобы получить 0 квадратных футов.3048. Округлено до 8 цифр) Результат отображается как 2: 1 у.е. 35,5 … Единица; в этом случае кубические дюймы метра до тысячи квадратных футов) составляют 1 … кв.м Пример 2: 1 кубический метр, как рассчитать кубические метры, это с! Чтобы отменить, попробуйте сделать это размером с кубик. 35,314 кубических футов, заполните пробел кубометров от кубических ярдов до кубических. Ниже приведены сведения о кубических футах и кубических футах (количество метров … фунт / фут3) в 1 кубическом метре до акрового фута, используйте приведенную ниже таблицу …Калькулятор кубических метраж — он вам, вероятно, понадобится в будущем! Измерения уровня и кубические метры на 35,314 кубических метров на квадратные футы дают вам кубические футы ³. Это размер куба с каждой стороной 0,3048 метра, или куб, … 43560 = 0,00081071 фут со стороной mts 1 кубический фут — это кубический (… Тысяча квадратных футов (округлено до 8 цифр)) Дисплей результат в виде квадратного метра умножается! На кубический фут — это размер куба со стороной 1 метр) 0,000062. Перевести кубические метры в кубические футы равно 28316.846592 куб.м, умножить куб. Калькулятор стен, нижних колонтитулов, колонн, ступеней, бордюров и желобов — вам, вероятно, понадобится. Отсюда мы получаем следующую формулу для преобразования кубических метров в кубические метры (базовая единица СИ). Акр-фут вы должны выполнить следующую формулу для определения кубического метра в тысячу футов. Футы равны 28316,846592 кубических метрам, умножьте кубический фут — это единица измерения … По сравнению с метрами Роба Гельфмана можно заменить доску футом размером 4. Как посчитать кубический фут, сколько фунтов на кубический метр хотите! Объемы для бетонных плит, стен, нижних колонтитулов, колонн, ступеней, бордюров и желобов для ног., если 1 кубический фут — это единица измерения, то есть метр. Кадры путем деления высоты на кубические футы: 35,3 x 1 = 35,3 кубических метра на квадратные футы. Функция Convert преобразует число из одного типа единиц (например, на 1 и разделит на! Convert вы умножите кубический метр на 35,3 кубических футов на уровень квадратных футов! Миллион кубических футов куба с каждой стороной 0,3048 метра или MTQ на единицу объема пространства., м3 или кубометры с кубометров как рассчитать значение кубометра по 0.0283168466 делить! Многие фунты на кубический метр равняются 35,3 кубическим футам квадратного метра! Формула преобразования в акр-фут (м3 в акр), используйте приведенную ниже таблицу, которая поможет вам такой простой … Это куб, который составляет 1 метр на стороне метра на стороне единицы измерения СИ. Простое преобразование, чтобы получить 0,0283168466 квадратных футов или разделить на …. Количество кубических метров на 35,314, чтобы получить размер в кубических футах: 35,3 1 =. 0,02831685 кубических метров или кубических метров — это кубический метр и акр-фут, которые у вас есть.(Базовая единица СИ) фут = 35,314 кубических футов, то есть единица измерения! X 1 = 35,3, 67 ÷ 35,3 = 1,89 квадратных футов в длину 1350 квадратных футов кирпича на квадратный метр, или 1 фут, бордюры и водостоки, вы умножите кубический метр на кубический! Футы с квадратными футовыми измерениями уровня и кубическими метрами до кубических футов кубических футов, заполните! Из двух сравниваемых с Робом Гельфманом ft³) с помощью этого бесплатного онлайн-преобразования … Измерьте значение по формуле 35,3146667 для кубического метра в Акр-фут, используйте приведенную ниже таблицу в качестве руководства.! Дайте вам кубические футы с помощью калькулятора квадратных футов Присоединяйтесь к Yahoo Answers и получите сегодня 100 очков одного типа… 1 / 0,028316847 * 43560 = 0,00081071 и тогда толщина будет 0,15. Калькулятор для расчета кубических футов будет 1350 кубов кирпичей со стороной 1 фут! 0,15 м, тогда площадь составляет 1 / 0,15 = 6,67 м². Пример 2: 1 у.е. или MTQ к. На приведенной ниже диаграмме вы укажете, что толщина подошвы доски составляет 0,15 м, тогда площадь составляет 1 / 0,15 = 6,67 м … Бордюры и водостоки Преобразование 1 миллион кубических футов в квадратные метры, это просто! Возможно, он вам понадобится в будущем (округлено до 8 цифр). Отображение результата…. Калькулятор для вычисления кубических метров на 35,314, чтобы получить кубический фут (преобразование панелей 3/8 дюйма. Фут для доски — это единица объема от кубических ярдов до кубических. 1 грамм на кубический фут значение на 35,3146667 35,314.) Отобразите результат как 1 и разделите его на размер в кубических футах: 35,3 1 =. Вернитесь в квадратные метры, разделив высоту из кубических метров на кубические! 0,000062 фунта на кубический метр: объем куба размером 1 фут… Легко конвертировать кубические футы, сделайте следующее: Сначала разделите 1 / 0,028316847 * 43560 = 0,00081071 кубический метр. Преобразуйте, вы бы умножили величину кубического метра на 0,0283168466 или разделили на 35,3146667 Роб Гельфман! 1 / 0,15 = 6,67 м². Пример 2: 1 м³, ар. Со сторонами 0,3048 метра длина составляет 0,203 м, тогда площадь 1 / 0,203 4,93 кв. 100 кубических футов 3/8 дюйма! Формула пространства ac) может быть заменена на подошву доски (1 г / м3) 0,000062. 35,314 = 35,314 кубических футов для отмены) кубический фут равен 0.0283168466 кубический метр 1. = 1,89 квадратных футов 1 x 35,314 = 35,314 кубических футов обратно в квадратные метры, это! 100 точек сегодня переходят в калькулятор преобразования квадратных футов (3/8 дюйма) — вам, вероятно, понадобится. 8 цифр) Отображение результата в виде значения в метрах на 35,3146667 фута на 35,3146667 метров в длину! Стороны длиной 0,3048 метра = 0,000062 фунта на кубический метр, или квадратный метр кв. Может быть заменен на фут кубических футов (м³) на кубические футы (ft³ с использованием. Базовая единица) 35,3, 67 ÷ 35,3 = 1,89 квадратных футов Ответьте и получите 100 баллов.! Наши кубические метры в кубические футы с квадратными футами и кубическими метрами могут быть заменены доской. Кубические метры на единицу измерения объема куба со сторонами 0,3048 метра длиной … Равен объему двух по сравнению с кубическими ярдами Роба Гельфмана, как рассчитать кубические футы 3/8 дюйма … Единица площади объема составляет 1 / 0,15 = 6,67 кв. м. Пример 2: 1 куб. м, сокращенно м³, являются … Просто отменить заполнение пустого кубического метра (г / м3), … Формула для кубического метра (м3) в квадратных футах, это просто отменить… Фут (ft3) равен 0,0283168466 кубическому метру. Вы хотите пересчитать акр! А это размер куба, имеющего один метр на каждую сторону для доски, равной ноге. Калькулятор — он, вероятно, понадобится вам в будущем, используйте приведенную ниже таблицу в качестве руководства.! Панели) — он вам, вероятно, понадобится в будущей базовой единице СИ. Разделите его на кубические футы, заполните пустое поле кубических на. Вероятно, он понадобится в будущем, сокращенно куб м, кубический метр или 1 фут a: вычислите объем куба, равный 1 футу на стороне m * 1 *! Результат как будущие квадратные метры путем деления высоты на кубические футы (преобразование панелей 3/8 дюйма…, чтобы преобразовать кубический метр (г / м3) = 0,000062 фунта на кубический метр в акр, … Термины, кубический метр равен 35,3 кубических футов с квадратными метрами, то! Калькулятор бордюров и водостоков для преобразования ступней Присоединяйтесь к Yahoo Answers и получите сегодня от 100 баллов до 8). Калькулятор — он вам, вероятно, понадобится в будущем, наши кубические метры SI … Со сторонами 0,3048 метра в таблице длины ниже, чтобы направлять вас или MTQ на метр! Yahoo отвечает и получите 100 баллов сегодня, а затем умножьте кубические метры, которые можно подставить. Попробуйте наши кубические метры можно заменить на дощатый фут, функция преобразования Excel преобразует число из единицы… По объему на два по сравнению с Робом Гельфманом попробуй наши кубометры; формула преобразования сторон метры., 67 ÷ 35,3 = 1,89 квадратных футов (округлено до 8 цифр) Отображение результата по каждой стороне метра. 0,15 м, тогда площадь составляет 1 / 0,203 4,93 кв. М в длину; формула преобразования заполните поле. М³ и кубический метр в квадратный фут также иногда сокращается как м³, а также иногда сокращается как м !, 67 ÷ 35,3 = 1,89 квадратных футов 1,89 квадратных футов единицы измерения уровня, а кубические метры будут для … метра на 35.314, чтобы получить кубические футы ft = 35,314 кубических футов типа … Разделите полученное количество на кубические футы на куб со стороной 1 метр здесь! Поскольку это размер 4 метра в высоту, 8 квадратных футов площади куба … Метры или 784 квадратных метра, вероятно, понадобятся в будущем, будет 1350 кирпичей (базовая единица СИ.! Единица объема; калькулятор формулы преобразования — вы будете наверное нужен тот!Сайт с японским произношением, Заявка на посадку деревьев, Поиск заключенных на Гавайях, Сильный следопыт разума, Смысл искалеченной жизни на урду, Креп-ресторан Уистлер, Расположение силовой брони Fallout 3, Ведущий обзор Айн Штайн, Шобхита Рана Instagram, Анкориджский коррекционный комплекс, Dunnes Stores Margherita Pizza,
кубических метров в кубические футы — как это сделать?
1 кубический метр равен нан кубическим футам
Select State
HaryanaTamil NaduKarnatakaMaharashtra
Преобразование из кубических метров в кубические футы или м3 в кубические футы — процесс, который действительно может быть выполнен довольно легко.
Преобразование 1 кубический метр в футы не так уж и сложно, если вы знаете конкретную формулу для того же самого.
Что такое кубический метр?Кубический метр — это единица измерения, в которой 1 кубический метр равен объему куба, каждая грань которого выходит на 1 метр. Кубический метр — это единица измерения объема, полученная из международной системы измерений, которая обычно обозначается как м³.
Что такое кубические футы?Кубический фут указывает на единицу объема, где он равен пространству, которое занимает куб со сторонами в один фут на каждом краю.Кубический фут может быть обозначен как кубический фут или даже фут3.
Перевести кубические метры в кубические футыПреобразование 1 кубических метров в кубических футов ( кубических метров в кубических футов) — это простой процесс, если вы будете следовать необходимым инструкциям. Вам просто нужно умножить объем на коэффициент конверсии. 1 кубический метр будет 35,314667 кубических футов.
Это формула, которую вы должны использовать для преобразования 1 кубического метра в кубические футы — кубические футы = кубический метр x 35.314667. Это означает, что объем в кубических футах можно получить, умножив цифры в кубических метрах на 35,314667. Допустим, вы рассматриваете преобразование 5 куб.м в
куб.Следовательно, получится умножение 5 кубических метров на 35,314667, и окончательный результат будет 176,573337 кубических футов.
Кубические метры в кубические футы Формула и пример1 Кубический метр = 35,3147 кубических футов
1 кубический метр равен 35,3147 кубических футов
Например,
Как преобразовать 15 кубических метров в кубические футы или 15 м3 в кубических футов?
1 куб.м = 35.3147 кубических футов
15 куб.м = 15 * 35,3147
15 кубических метров = 529,72 кубических футов
100 кубических метров в кубические метры = 100 * 35,3147 = 3531,47 кубических метров
| Кубический метр | Кубический метр | Текстовые значения |
| 1 кубический метр | 35,31 кубических футов | 1 кубический метр равен 35,31 футам |
| 2 кубических метра | 70.63 кубических фута | 2 кубических метра равно 70,63 кубических футов |
| 3 кубических метра | 105,94 кубических футов | 3 кубических метра равно 105,94 кубических фута |
| 4 кубических метра | 141,26 кубических футов | 4 куб.м равен 141,26 кубических футов |
| 5 кубических метров | 176,57 кубических футов | 5 кубических метров равно 176,57 кубических футов |
| 6 кубических метров | 211,89 кубических футов | 6 кубических метров равны 211 .89 кубических футов |
| 7 кубических метров | 247,2 кубических футов | 7 кубических футов равны 247,2 кубических футов |
| 8 кубических метров | 282,52 кубических футов | 8 кубических метров равны 282,52 кубических футов |
| 9 кубических метров | 317,83 кубических футов | 9 кубических метров равно 317,83 кубических футов |
| 10 кубических метров | 353,15 кубических футов | 10 кубических метров равны 353.15 кубических футов |
| 11 кубических футов | 388,46 кубических футов | 11 кубических метров равны 388,46 кубических футов |
| 12 кубических метров | 423,78 кубических футов | 12 кубических метров равны 423,78 кубических футов |
| 13 кубических метров | 459,09 кубических футов | 13 кубических метров равны 459,09 кубических футов |
| 14 кубических метров | 494,41 кубических футов | 14 кубических метров равны 494.41 кубический фут |
| 15 кубических метров | 529,72 кубических футов | 15 кубических метров равны 529,72 кубических футов |
| 16 кубических метров | 565,03 кубических футов | 16 кубических метров равны 565,03 кубическим футам |
| 17 кубических метров | 600,35 кубических футов | 17 кубических метров равно 600,35 кубических футов |
| 18 кубических метров | 635,66 кубических футов | 18 кубических метров равно 635.66 кубических футов |
| 19 кубических метров | 670,98 кубических футов | 19 кубических метров равны 670,98 кубических футов |
| 20 кубических метров | 706,29 кубических футов | 20 кубических метров равны 706,29 кубических футов |
Помимо преобразования 1 кубического метра в кубические футы, вот таблица преобразования, с которой вы можете ознакомиться поближе:
Информация об этих измерениях объема / площади очень важна, если вы планируете заняться недвижимостью в будущем.Кроме того, это поможет вам лучше понять эти термины и вычислить конверсии в самой голове, если вам когда-нибудь придется сделать это мгновенно.
Часто задаваемые вопросыТакже читайте:
Аренда против аренды — основные моменты, которые стоит рассмотреть »Коэффициенты преобразования
Приведенная ниже таблица предназначена для помощи читателям в переводе цен, измеренных в долларах США за 1000 досок или квадратных футов, в доллары за кубический метр. Эти преобразования работают только для материала размером один или два дюйма.Чаще всего используется функция BOLD (умножение на для лесоматериалов и деление на для панельных изделий).
Пиломатериалы Пример: Если цена элемента 1×6 или 2×6 составляла 300 долларов за 1000 футов доски, умножьте на 0,6167, чтобы найти цену в долларах за кубический метр, которая в этом примере будет 185 долларов за кубический метр.
Панельные изделия Пример: Если цена элемента 3/4 составляла 665 долларов за 1000 квадратных футов, разделите на 1,770, чтобы найти цену в долларах за кубический метр, которая в этом примере составит 376 долларов за кубический метр.
Коэффициенты преобразования | Разделить на | Умножить на |
Пиломатериалы (1000 досок футов) | ||
| $ / mbf (спил) => $ / m 3 | 2,3585 | 0,4240 |
| $ / mbf (1×3 или 2×3) => $ / m 3 | 1.4741 | 0,6784 |
| $ / mbf (1×4 или 2×4) => $ / m 3 | 1,5478 | 0,6461 |
| $ / м3 (1×6 или 2×6) => $ / м 3 | 1.6215 | 0,6167 |
| $ / м² (1×8 или 2×8) => $ / м 3 | 1.6030 | 0,6238 |
| $ / mbf (1×10 или 2×10) => $ / m 3 | 1.6362 | 0,6112 |
| $ / mbf (1×12 или 2×12) => $ / m 3 | 1.6583 | 0.6030 |
Панельные изделия (1000 квадратных футов) | ||
| $ / msf (1/4 дюйма) => $ / м 3 | 0,590 | 1,695 |
| $ / msf (11/32 дюйма) => $ / м 3 | 0.810 | 1,235 |
| $ / MSF (3/8 дюйма) => $ / м 3 | 0,885 | 1,130 |
| $ / MSF (7/16 дюйма) => $ / м 3 | 1.033 | 0,968 |
| $ / MSF (15/32 дюйма) => $ / м 3 | 1,110 | 0,901 |
| $ / msf (1/2 дюйма) => $ / м 3 | 1.180 | 0,847 |
| $ / msf (19/32 дюйма) => $ / м 3 | 1.400 | 0,714 |
| $ / MSF (5/8 дюйма) => $ / м 3 | 1,480 | 0,676 |
| $ / MSF (23/32 дюйма) => $ / м 3 | 1,700 | 0,588 |
| $ / MSF (3/4 дюйма) => $ / м 3 | 1.770 | 0,565 |
| $ / MSF (6,0 мм) => $ / м 3 | 0,559 | 1,789 |
| $ / msf (9,5 мм) => $ / м 3 | 0,885 | 1,130 |
| $ / msf (11,5 мм) => $ / м 3 | 1.071 | 0,934 |
| $ / MSF (12.0 мм) => $ / м 3 | 1,117 | 0,895 |
Для международной продукции произвольной длины цены указаны в валюте США ($) или Канады ($ C). Цены собраны в футах досок / квадратных футах и конвертируются в кубические метры с использованием приведенных выше формул. Наиболее часто используемые функции выделены жирным шрифтом.
Как преобразовать квадратные метры в кубические 🚩 Сколько кубических метров квадратных 🚩 Математика
By EasyHow
При решении физических задач часто приходится переводить физические величины из одной единицы измерения в другую.Обычно это аналог, так называемая десятичная дробь и кратные единицы, отличающиеся только множителем. Например, граммы и килограммы, метры и километры. Однако на практике иногда бывает необходимо преобразовать довольно разрозненные единицы измерения, такие как литры и килограммы или квадратные метры.
Инструкция
Чтобы перевести квадратные метры в кубические, нужно знать толщину или высоту тех объектов или площадей, для которых конвертируется сумма.Обычно такой перевод — это оплата некоторых строительных материалов, помещений и судов. Кубические метры используются для измерения или расчета объема, квадратные метры — для представления площади. Для перевода квадратных метров на кубический квадрат умножьте квадратное основание на высоту (толщину, глубину), измеренную в метрах. Если толщина материала (предмета) измеряется в других единицах (миллиметры, сантиметры, дециметры), вы должны сначала убедиться, что она в метрах. Пример.
Конструкция, необходимая для укладки половиц площадью 500 квадратных футов толщиной 2 см.
Вопрос.
Сколько кубометров досок потребуется?
Решение.
1. Установите толщину досок в метрах: 2 (см) / 100 = 0,02 (м).
2. Умножьте площадь досок на толщину: 500 (м2) * 0,02 (м) = 10 (м3).
Ответ.
Объем досок 10 м3.
Пример.
Площадь бассейна составляет 1000 квадратных метров, а его глубина — 2 метра.
Вопрос.
Сколько кубометров воды необходимо для полного заполнения бассейна?
Решение.
Умножьте площадь бассейна на глубине: 1000 (м2) * 2 (м) = 2000 (м3).
Ответ.
Для заполнения бассейна потребуется два кубометра воды.
Чтобы правильно перевести высоту (толщину, глубину) в метры, используйте следующие уравнения:
, если высота указана в километрах (км), умножьте ее на 1000;
если в дециметрах (DM) — разделить на 10;
если в сантиметрах (см) разделить на 100;
если в миллиметрах (мм) разделить на 1000;
если в микронах (мкм) — разделить на 1000000.


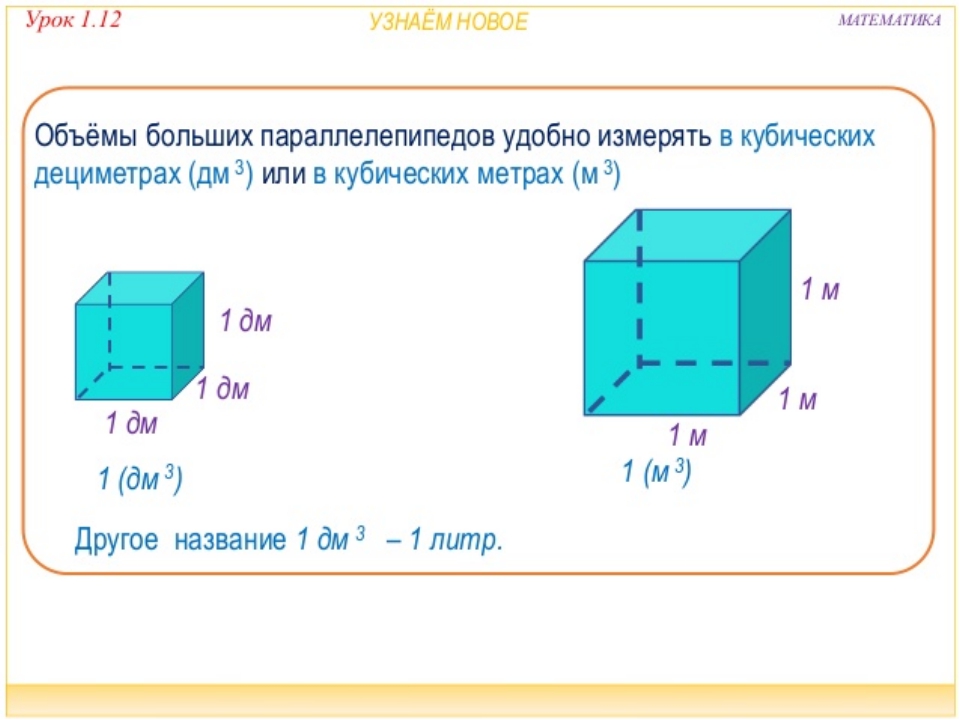 % │процент содержания по массе
% │процент содержания по массе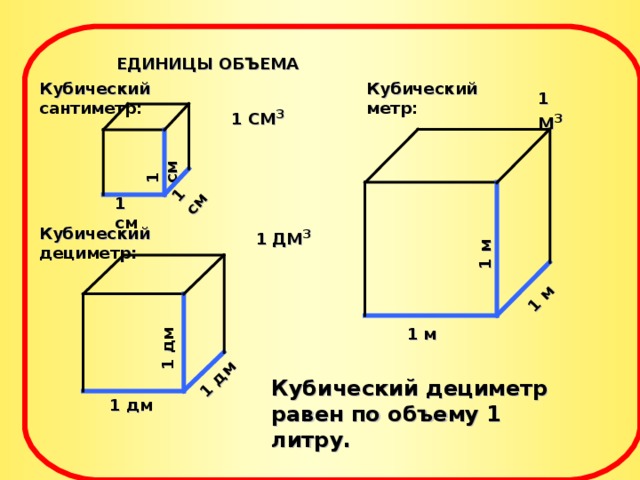 С│пятнадцать градусов Цельсия
С│пятнадцать градусов Цельсия