Расчет инсоляции и коэффициента естественной освещенности (КЕО)
Инсоляция – достаточность попадания прямого солнечного света внутрь помещений или на участки местности для обеспечения комфортного проживания людей.
Коэффициент естественной освещенности (КЕО) — величина отношения световой энергии, попадающей в расчетную точку внутри помещения в конкретных условиях застройки, к величине световой энергии, которая попадала бы в расчетную точку в условиях, что та находилась бы под открытым небом.
Расчеты инсоляции и коэффициента естественной освещенности (КЕО) — два основных вида светотехнических расчетов, применяемых при выборе и обосновании архитектурных решений, и являются обязательным разделом в составе предпроектной и проектной документации согласно Федеральному закону №52 “О санитарно-эпидемиологическом благополучии населения”, который проходит государственную экспертизу. Положительное заключение на материалы расчета инсоляции в составе проектной документации является основанием для выдачи Разрешения на производство строительно-монтажных работ.
При проектировании зданий в уже существующей плотной урбанизированной застройке вопрос о нормах инсоляции помещений стоит крайне остро, особенно в центральной части города. Достаточно одного помещения, не удовлетворяющего нормам инсоляции или КЕО, и у инспектирующей организации будет серьезный аргумент дать отрицательное заключение на проект.
ООО «ИнЭКо «Е1» проводит расчеты инсоляции и КЭО любой сложности. В соответствии с требованиями Заказчика может быть проведен анализ существующей ситуации и предложены возможности надстройки или расширения существующих зданий с оценкой соответствия действующим нормативам.
Расчеты инсоляции и коэффициента естественной освещенности выполняются автоматизировано с помощью специализированной компьютерной программы, благодаря чему Вы получаете более точный и быстрый расчет. По результатам расчета инсоляции составляется технический отчет с оценкой условий освещенности помещений, находящихся в наихудших условиях, рекомендациями о возможностях надстройки над существующим зданием и оценкой соответствия действующим нормативам (СанПиН 2. 2.1/2.1.1.1076-01 «Гигиенические требования к инсоляции и солнцезащите помещений жилых и общественных зданий и территорий» и СанПиН 2.2.1/2.1.1.1278-03 “Гигиенические требования к естественному, искусственному и совмещенному освещению жилых и общественных зданий”).
2.1/2.1.1.1076-01 «Гигиенические требования к инсоляции и солнцезащите помещений жилых и общественных зданий и территорий» и СанПиН 2.2.1/2.1.1.1278-03 “Гигиенические требования к естественному, искусственному и совмещенному освещению жилых и общественных зданий”).
|
Город |
Географическое положение |
|
Москва |
55° 45′ с.ш. 37° 37′ в.д. |
|
Санкт-Петербург |
59° 56′ с.ш. 30° 19′ в.д. |
|
Новосибирск |
55° 1′ с.ш. 82° 56′ в.д. |
|
Екатеринбург |
56° 51′ с.ш. 60° 36′ в.д. |
|
Самара |
53° 14′ с. |
|
Омск |
54° 59′ с.ш. 73° 22′ в.д. |
|
Казань |
55° 47′ с.ш. 49° 10′ в.д. |
|
Уфа |
54° 49′ с.ш. 56° 4′ в.д. |
|
Челябинск |
55° 9′ с.ш. 61° 26′ в.д. |
|
Ростов-на-Дону |
47° 14′ с.ш. 39° 42′ в.д. |
|
Пермь |
58° 0′ с.ш. 56° 14′ в.д. |
|
Волгоград |
48° 43′ с.ш. 44° 29′ в.д. |
|
Воронеж |
51° 43′ с.ш. 39° 16′ в.д. |
|
Красноярск |
56° 1′ с.ш. |
|
Саратов |
51° 33′ с.ш. 46° 0′ в.д. |
|
Тольятти |
53° 29′ с.ш. 49° 31′ в.д. |
|
Ульяновск |
54° 19′ с.ш. 48° 22′ в.д. |
|
Ижевск |
56° 50′ с.ш. 53° 11′ в.д. |
|
Краснодар |
45° 2′ с.ш. 38° 58′ в.д. |
|
Ярославль |
57° 37′ с.ш. 39° 51′ в.д. |
|
Хабаровск |
48° 25′ с.ш. 135° 7′ в.д. |
|
Владивосток |
43° 8′ с.ш. 131° 54′ в.д. |
|
Иркутск |
52° 20′ с. |
|
Барнаул |
53° 21′ с.ш. 83° 45′ в.д. |
|
Новокузнецк |
53° 45′ с.ш. 87° 7′ в.д. |
|
Липецк |
52° 37′ с.ш. 39° 37′ в.д. |
|
Пенза |
53° 12′ с.ш. 45° 0′ в.д. |
|
Рязань |
54° 36′ с.ш. 39° 42′ в.д. |
|
Оренбург |
51° 47′ с.ш. 55° 6′ в.д. |
|
Набережные Челны |
55° 41′ с.ш. 52° 19′ в.д. |
|
Тюмень |
57° 10′ с.ш. 65° 30′ в.д. |
|
Тула |
54° 13′ с. |
|
Кемерово |
55° 25′ с.ш. 86° 5′ в.д. |
|
Астрахань |
46° 22′ с.ш. 48° 5′ в.д. |
|
Томск |
56° 29′ с.ш. 84° 59′ в.д. |
|
Киров |
58° 36′ с.ш. 49° 39′ в.д. |
|
Чебоксары |
56° 8′ с.ш. 47° 14′ в.д. |
|
Брянск |
53° 16′ с.ш. 34° 25′ в.д. |
|
Иваново |
57° 1′ с.ш. 40° 59′ в.д. |
|
Тверь |
56° 52′ с.ш. 35° 55′ в.д. |
|
Курск |
51° 44′ с.ш. 36° 11′ в. |
|
Магнитогорск |
53° 25′ с.ш. 58° 58′ в.д. |
|
Калининград |
54° 43′ с.ш. 20° 31′ в.д. |
|
Нижний Тагил |
57° 56′ с.ш. 60° 1′ в.д. |
|
Улан-Удэ |
51° 50′ с.ш. 107° 36′ в.д. |
|
Сочи |
43° 35′ с.ш. 39° 44′ в.д. |
|
Курган |
55° 26′ с.ш. 65° 19′ в.д. |
|
Мурманск |
68° 58′ с.ш. 33° 5′ в.д. |
|
Архангельск |
64° 32′ с.ш. 40° 32′ в.д. |
|
Смоленск |
54° 47′ с. |
|
|
50° 37′ с.ш. 36° 35′ в.д. |
|
Ставрополь |
45° 3′ с.ш. 41° 58′ в.д. |
|
Орел |
52° 58′ с.ш. 36° 4′ в.д. |
|
Калуга |
54° 32′ с.ш. 36° 17′ в.д. |
|
Владимир |
56° 9′ с.ш. 40° 25′ в.д. |
|
Махачкала |
42° 59′ с.ш. 47° 31′ в.д. |
|
Череповец |
|
|
Владикавказ |
43° 2′ с.ш. 44° 40′ в.д. |
|
Саранск |
54° 11′ с. |
|
Тамбов |
52° 43′ с.ш. 41° 25′ в.д. |
|
Чита |
52° 3′ с.ш. 113° 28′ в.д. |
|
Вологда |
59° 14′ с.ш. 39° 54′ в.д. |
|
Кострома |
57° 46′ с.ш. 40° 56′ в.д. |
|
Комсомольск-на-Амуре |
50° 34′ с.ш. 137° 0′ в.д. |
|
Волжский |
48° 49′ с.ш. 44° 44′ в.д. |
|
Таганрог |
47° 14′ с.ш. 38° 54′ в.д. |
|
Петрозаводск |
61° 47′ с.ш. 34° 20′ в.д. |
|
Братск |
56° 18′ с. |
|
Сургут |
61° 15′ с.ш. 73° 23′ в.д. |
|
Дзержинск |
56° 16′ с.ш. 43° 24′ в.д. |
|
Орск |
51° 13′ с.ш. 58° 38′ в.д. |
|
Стерлитамак |
53° 38′ с.ш. 55° 57′ в.д. |
|
Ангарск |
52° 34′ с.ш. 103° 55′ в.д. |
|
Йошкар-Ола |
56° 38′ с.ш. 47° 52′ в.д. |
|
Рыбинск |
58° 3′ с.ш. 38° 50′ в.д. |
|
Прокопьевск |
53° 54′ с.ш. 86° 43′ в.д. |
|
Нижневартовск |
60° 56′ с. |
|
Великий Новгород |
58° 32′ с.ш. 31° 16′ в.д. |
|
Сыктывкар |
61° 40′ с.ш. 50° 49′ в.д. |
|
Нижнекамск |
55° 38′ с.ш. 51° 47′ в.д. |
|
Бийск |
52° 32′ с.ш. 85° 10′ в.д. |
|
Благовещенск |
50° 17′ с.ш. 127° 32′ в.д. |
|
Северодвинск |
64° 34′ с.ш. 39° 49′ в.д. |
|
Шахты |
47° 41′ с.ш. 40° 15′ в.д. |
|
Старый Оскол |
51° 18′ с.ш. 37° 50′ в.д. |
|
Зеленоград |
55° 56′ с. |
|
Новороссийск |
44° 43′ с.ш. 37° 46′ в.д. |
|
Балаково |
52° 0′ с.ш. 47° 47′ в.д. |
|
Псков |
57° 49′ с.ш. 28° 20′ в.д. |
|
Златоуст |
55° 11′ с.ш. 59° 38′ в.д. |
|
Якутск |
62° 10′ с.ш. 129° 50′ в.д. |
|
Подольск |
55° 26′ с.ш. 37° 34′ в.д. |
|
Энгельс |
51° 29′ с.ш. 46° 8′ в.д. |
|
Сызрань |
53° 10′ с.ш. 48° 27′ в.д. |
|
Каменск-Уральский |
56° 25′ с. |
|
Петропавловск-Камчатский |
53° 2′ с.ш. 158° 38′ в.д. |
|
Новочеркасск |
47° 25′ с.ш. 40° 5′ в.д. |
|
Березники |
59° 25′ с.ш. 56° 46′ в.д. |
|
Южно-Сахалинск |
46° 58′ с.ш. 142° 44′ в.д. |
|
Волгодонск |
47° 31′ с.ш. 42° 8′ в.д. |
|
Абакан |
53° 44′ с.ш. 91° 26′ в.д. |
|
Обнинск |
55° 6′ с.ш. 36° 37′ в.д. |
|
Майкоп |
44° 37′ с.ш. 40° 5′ в.д. |
|
Армавир |
44° 59′ с. |
|
Миасс |
55° 0′ с.ш. 60° 5′ в.д. |
|
Люберцы |
55° 40′ с.ш. 37° 57′ в.д. |
|
Рубцовск |
51° 32′ с.ш. 81° 12′ в.д. |
|
Ковров |
56° 22′ с.ш. 41° 20′ в.д. |
|
Салават |
53° 24′ с.ш. 55° 53′ в.д. |
|
Мытищи |
55° 54′ с.ш. 37° 45′ в.д. |
|
Находка |
42° 49′ с.ш. 132° 53′ в.д. |
|
Уссурийск |
43° 49′ с.ш. 131° 58′ в.д. |
|
Коломна |
55° 5′ с. |
|
Электросталь |
55° 46′ с.ш. 38° 28′ в.д. |
|
Колпино |
59° 45′ с.ш. 30° 36′ в.д. |
|
Альметьевск |
54° 54′ с.ш. 52° 19′ в.д. |
|
Муром |
55° 34′ с.ш. 42° 2′ в.д. |
|
Димитровград |
54° 14′ с.ш. 49° 35′ в.д. |
|
Новомосковск |
54° 5′ с.ш. 38° 11′ в.д. |
|
Первоуральск |
56° 55′ с.ш. 59° 57′ в.д. |
|
Норильск |
69° 19′ с.ш. 88° 11′ в.д. |
|
Пятигорск |
44° 2′ с. |
|
Невинномысск |
44° 38′ с.ш. 41° 56′ в.д. |
|
Химки |
55° 53′ с.ш. 37° 26′ в.д. |
|
Балашиха |
55° 50′ с.ш. 37° 57′ в.д. |
|
Королёв |
55° 55′ с.ш. 37° 49′ в.д. |
|
Серпухов |
54° 55′ с.ш. 37° 26′ в.д. |
|
Одинцово |
55° 40′ с.ш. 37° 17′ в.д. |
|
Орехово-Зуево |
55° 48′ с.ш. 38° 58′ в.д. |
|
Грозный |
43° 19′ с.ш. 45° 41′ в.д. |
|
Камышин |
50° 6′ с. |
|
Кисловодск |
43° 54′ с.ш. 42° 43′ в.д. |
|
Новочебоксарск |
56° 7′ с.ш. 47° 29′ в.д. |
|
Черкесск |
44° 17′ с.ш. 42° 4′ в.д. |
|
Ачинск |
56° 16′ с.ш. 90° 29′ в.д. |
|
Северск |
56° 37′ с.ш. 84° 52′ в.д. |
|
Назрань |
43° 13′ с.ш. 44° 48′ в.д. |
|
Елец |
52° 36′ с.ш. 38° 31′ в.д. |
|
Мичуринск |
52° 54′ с.ш. 40° 28′ в.д. |
|
Ногинск |
55° 52′ с. |
|
Новокуйбышевск |
53° 6′ с.ш. 49° 53′ в.д. |
|
Великие Луки |
56° 20′ с.ш. 30° 31′ в.д. |
|
Нефтекамск |
56° 7′ с.ш. 54° 16′ в.д. |
|
Магадан |
59° 34′ с.ш. 150° 47′ в.д. |
|
Октябрьский |
54° 28′ с.ш. 53° 28′ в.д. |
|
Ленинск-Кузнецкий |
54° 40′ с.ш. 86° 10′ в.д. |
|
Сергиев Посад |
56° 19′ с.ш. 38° 8′ в.д. |
|
Арзамас |
55° 23′ с.ш. 43° 50′ в.д. |
|
Новотроицк |
51° 13′ с.ш. 58° 21′ в.д. |
|
Киселёвск |
53° 59′ с.ш. 86° 39′ в.д. |
|
Глазов |
58° 8′ с.ш. 52° 38′ в.д. |
|
Канск |
56° 13′ с.ш. 95° 43′ в.д. |
|
Соликамск |
59° 38′ с.ш. 56° 46′ в.д. |
|
Элиста |
46° 19′ с.ш. 44° 13′ в.д. |
|
Сарапул |
56° 28′ с.ш. 53° 48′ в.д. |
|
Междуреченск |
53° 41′ с.ш. 88° 5′ в.д. |
|
Щёлково |
55° 54′ с.ш. 38° 1′ в.д. |
|
Усть-Илимск |
58° 0′ с.ш. 102° 40′ в.д. |
|
Кызыл |
51° 43′ с.ш. 94° 23′ в.д. |
|
Усолье-Сибирское |
52° 46′ с.ш. 103° 38′ в.д. |
|
Воткинск |
57° 3′ с.ш. 53° 59′ в.д. |
|
Новошахтинск |
47° 46′ с.ш. 39° 56′ в.д. |
|
Железнодорожный |
55° 45′ с.ш. 38° 8′ в.д. |
|
Ессентуки |
44° 2′ с.ш. 42° 51′ в.д. |
|
Зеленодольск |
55° 50′ с.ш. 48° 40′ в.д. |
|
Серов |
59° 37′ с.ш. 60° 35′ в.д. |
|
Кинешма |
57° 27′ с.ш. 42° 8′ в.д. |
|
Тобольск |
58° 11′ с.ш. 68° 14′ в.д. |
|
Ноябрьск |
63° 10′ с.ш. 75° 37′ в.д. |
|
Балашов |
51° 32′ с.ш. 43° 10′ в.д. |
|
Железногорск |
52° 21′ с.ш. 35° 25′ в.д. |
|
Кузнецк |
53° 7′ с.ш. 46° 34′ в.д. |
|
Батайск |
47° 8′ с.ш. 39° 45′ в.д. |
|
Дербент |
42° 4′ с.ш. 48° 17′ в.д. |
|
Нефтеюганск |
55° 6′ с.ш. 54° 17′ в.д. |
|
Жуковский |
55° 33′ с.ш. 38° 15′ в.д. |
|
Ухта |
63° 34′ с.ш. 53° 43′ в.д. |
|
Анжеро-Судженск |
56° 5′ с.ш. 86° 1′ в.д. |
|
Бугульма |
54° 32′ с.ш. 52° 48′ в.д. |
|
Новоуральск |
57° 15′ с.ш. 59° 48′ в.д. |
|
Красногорск |
55° 50′ с.ш. 37° 20′ в.д. |
|
Чайковский |
56° 46′ с.ш. 54° 5′ в.д. |
|
Новый Уренгой |
66° 5′ с.ш. 76° 31′ в.д. |
|
Губкинский |
64° 26′ с.ш. 76° 29′ в.д. |
|
Кирово-Чепецк |
58° 33′ с.ш. 50° 2′ в.д. |
|
Клин |
56° 20′ с.ш. 36° 42′ в.д. |
|
Хасавюрт |
43° 15′ с.ш. 46° 35′ в.д. |
|
Раменское |
55° 29′ с.ш. 38° 21′ в.д. |
|
Губкин |
51° 17′ с.ш. 37° 23′ в.д. |
|
Озёрск |
55° 46′ с.ш. 60° 42′ в.д. |
|
Пушкин |
59° 46′ с.ш. 30° 19′ в.д. |
|
Ейск |
46° 42′ с.ш. 38° 16′ в.д. |
|
Бузулук |
52° 47′ с.ш. 52° 16′ в.д. |
|
Шадринск |
56° 5′ с.ш. 63° 37′ в.д. |
|
Бердск |
54° 46′ с.ш. 83° 5′ в.д. |
|
Троицк |
54° 7′ с.ш. 61° 34′ в.д. |
|
Воркута |
67° 31′ с.ш. 64° 2′ в.д. |
|
Юрга |
55° 44′ с.ш. 84° 55′ в.д. |
|
Кропоткин |
45° 26′ с.ш. 40° 34′ в.д. |
|
Свободный |
51° 23′ с.ш. 128° 8′ в.д. |
|
Каменск-Шахтинский |
48° 19′ с.ш. 40° 15′ в.д. |
|
Ишимбай |
53° 27′ с.ш. 56° 3′ в.д. |
|
Реутов |
55° 46′ с.ш. 37° 52′ в.д. |
|
Каспийск |
42° 53′ с.ш. 47° 38′ в.д. |
|
Егорьевск |
55° 23′ с.ш. 39° 2′ в.д. |
|
Гусь-Хрустальный |
55° 37′ с.ш. 40° 39′ в.д. |
|
Копейск |
55° 8′ с.ш. 61° 39′ в.д. |
|
Белорецк |
53° 58′ с.ш. 58° 24′ в.д. |
|
Белогорск |
50° 55′ с.ш. 128° 28′ в.д. |
|
Лысьва |
58° 7′ с.ш. 57° 47′ в.д. |
|
Кунгур |
57° 26′ с.ш. 56° 56′ в.д. |
|
Минеральные Воды |
44° 13′ с.ш. 43° 8′ в.д. |
|
Биробиджан |
48° 48′ с.ш. 132° 55′ в.д. |
|
Черногорск |
53° 50′ с.ш. 91° 13′ в.д. |
|
Воскресенск |
55° 19′ с.ш. 38° 42′ в.д. |
|
Белово |
54° 25′ с.ш. 86° 17′ в.д. |
|
Выборг |
60° 43′ с.ш. 28° 46′ в.д. |
|
Асбест |
57° 1′ с.ш. 61° 28′ в.д. |
|
Азов |
47° 6′ с.ш. 39° 26′ в.д. |
|
Гатчина |
59° 34′ с.ш. 30° 6′ в.д. |
|
Петергоф |
59° 53′ с.ш. 29° 54′ в.д. |
|
Чапаевск |
52° 58′ с.ш. 49° 41′ в.д. |
|
Саров |
55° 23′ с.ш. 43° 50′ в.д. |
|
Нижний Новгород |
56° 19′ с.ш. 44° 0′ в.д. |
|
Гуково |
48° 4′ с.ш. 39° 56′ в.д. |
|
Павловский Посад |
55° 46′ с.ш. 38° 40′ в.д. |
|
Артем |
43° 22′ с.ш. 132° 11′ в.д. |
|
Шуя |
56° 52′ с.ш. 41° 21′ в.д. |
|
Ступино |
54° 53′ с.ш. 38° 7′ в.д. |
|
Апатиты |
67° 34′ с.ш. 33° 23′ в.д. |
|
Арсеньев |
44° 10′ с.ш. 133° 17′ в.д. |
|
Ревда |
56° 49′ с.ш. 59° 57′ в.д. |
|
Борисоглебск |
51° 22′ с.ш. 42° 5′ в.д. |
|
Котлас |
61° 16′ с.ш. 46° 39′ в.д. |
|
Лабинск |
44° 38′ с.ш. 40° 43′ в.д. |
|
Славянск-на-Кубани |
45° 15′ с.ш. 38° 7′ в.д. |
|
Краснотурьинск |
59° 47′ с.ш. 60° 29′ в.д. |
|
Будённовск |
44° 47′ с.ш. 44° 8′ в.д. |
|
Россошь |
50° 13′ с.ш. 39° 35′ в.д. |
|
Туймазы |
54° 36′ с.ш. 53° 42′ в.д. |
|
Сальск |
46° 28′ с.ш. 41° 32′ в.д. |
|
Дмитров |
56° 21′ с.ш. 37° 32′ в.д. |
|
Щёкино |
54° 1′ с.ш. 37° 31′ в.д. |
|
Мелеуз |
52° 58′ с.ш. 55° 56′ в.д. |
|
Заречный |
53° 8′ с.ш. 46° 35′ в.д. |
|
Бор |
56° 21′ с.ш. 44° 5′ в.д. |
|
Ишим |
56° 7′ с.ш. 69° 28′ в.д. |
|
Назарово |
56° 1′ с.ш. 90° 23′ в.д. |
|
Выкса |
55° 19′ с.ш. 42° 10′ в.д. |
|
Балахна |
56° 29′ с.ш. 43° 38′ в.д. |
|
Талнах |
69° 30′ с.ш. 88° 27′ в.д. |
|
Волжск |
55° 51′ с.ш. 48° 31′ в.д. |
|
Белебей |
54° 7′ с.ш. 54° 7′ в.д. |
|
Боровичи |
58° 24′ с.ш. 33° 54′ в.д. |
|
Крымск |
44° 56′ с.ш. 37° 58′ в.д. |
|
Новоалтайск |
53° 24′ с.ш. 83° 56′ в.д. |
|
Сибай |
52° 43′ с.ш. 58° 40′ в.д. |
|
Нягань |
62° 9′ с.ш. 65° 23′ в.д. |
|
Осинники |
53° 37′ с.ш. 87° 20′ в.д. |
|
Отрадный |
53° 20′ с.ш. 51° 22′ в.д. |
|
Тулун |
54° 34′ с.ш. 100° 34′ в.д. |
|
Верхняя Салда |
58° 4′ с.ш. 60° 33′ в.д. |
|
Амурск |
50° 14′ с.ш. 136° 53′ в.д. |
|
Рузаевка |
54° 4′ с.ш. 44° 57′ в.д. |
|
Чебаркуль |
54° 59′ с.ш. 60° 22′ в.д. |
|
Берёзовский |
55° 40′ с.ш. 86° 16′ в.д. |
|
Сатка |
55° 2′ с.ш. 59° 2′ в.д. |
|
Инта |
66° 2′ с.ш. 60° 10′ в.д. |
|
Можга |
56° 27′ с.ш. 52° 11′ в.д. |
|
Радужный |
62° 5′ с.ш. 77° 14′ в.д. |
|
Лесозаводск |
45° 29′ с.ш. 133° 25′ в.д. |
|
Красноуфимск |
56° 37′ с.ш. 57° 45′ в.д. |
|
Каменка |
53° 11′ с.ш. 44° 2′ в.д. |
|
Мыски |
53° 44′ с.ш. 87° 47′ в.д. |
|
Красный Сулин |
47° 53′ с.ш. 40° 4′ в.д. |
|
Тавда |
58° 3′ с.ш. 65° 16′ в.д. |
|
Камень-на-Оби |
53° 48′ с.ш. 81° 19′ в.д. |
|
Заинск |
55° 19′ с.ш. 52° 3′ в.д. |
|
Стрежевой |
60° 44′ с.ш. 77° 33′ в.д. |
|
Пугачёв |
52° 1′ с.ш. 48° 48′ в.д. |
|
Шарыпово |
55° 32′ с.ш. 89° 12′ в.д. |
|
Нижнеудинск |
54° 54′ с.ш. 99° 1′ в.д. |
|
Коркино |
54° 54′ с.ш. 61° 22′ в.д. |
|
Реж |
57° 22′ с.ш. 61° 24′ в.д. |
|
Пыть-Ях |
60° 45′ с.ш. 72° 56′ в.д. |
|
Кушва |
58° 18′ с.ш. 59° 44′ в.д. |
|
Мегион |
61° 3′ с.ш. 76° 6′ в.д. |
|
Артёмовский |
57° 21′ с.ш. 61° 52′ в.д. |
|
Южноуральск |
54° 26′ с.ш. 61° 14′ в.д. |
|
Кыштым |
55° 43′ с.ш. 60° 32′ в.д. |
|
Бирск |
55° 25′ с.ш. 55° 33′ в.д. |
|
Большой Камень |
43° 7′ с.ш. 132° 20′ в.д. |
|
Лангепас |
61° 10′ с.ш. 75° 23′ в.д. |
|
Мариинск |
56° 13′ с.ш. 87° 43′ в.д. |
|
Добрянка |
58° 28′ с.ш. 56° 25′ в.д. |
|
Учалы |
54° 18′ с.ш. 59° 26′ в.д. |
|
Холмск |
47° 3′ с.ш. 142° 2′ в.д. |
|
Ялуторовск |
56° 39′ с.ш. 66° 17′ в.д. |
|
Чернушка |
56° 31′ с.ш. 56° 4′ в.д. |
|
Урай |
60° 8′ с.ш. 64° 46′ в.д. |
|
Аша |
54° 59′ с.ш. 57° 17′ в.д. |
|
Ханты-Мансийск |
60° 59′ с.ш. 69° 0′ в.д. |
|
Муравленко |
63° 54′ с.ш. 74° 34′ в.д. |
|
Верхний Уфалей |
56° 4′ с.ш. 60° 14′ в.д. |
|
Барабинск |
55° 21′ с.ш. 78° 20′ в.д. |
|
Зима |
53° 55′ с.ш. 102° 3′ в.д. |
|
Богданович |
56° 47′ с.ш. 62° 1′ в.д. |
|
Сухой Лог |
56° 55′ с.ш. 62° 1′ в.д. |
|
Карпинск |
59° 46′ с.ш. 59° 59′ в.д. |
|
Североуральск |
60° 11′ с.ш. 59° 58′ в.д. |
|
Славгород |
53° 0′ с.ш. 78° 38′ в.д. |
|
Салехард |
66° 32′ с.ш. 66° 35′ в.д. |
Как правильно рассчитать параметры солнечных панелей для дома
Чтобы правильно произвести расчет параметров солнечных панелей для жилого дома, первым делом нужно обратить внимание на удаленность жилья от линий электропередач. Такой важный параметр, как целесообразность фотоэлектрической установки, растет с удалением жилья от ЛЭП.
Также можно сказать, что экономическая обоснованность устройства солнечных батарей начинается в случае удаления линии централизованного электричества на расстояние не менее 1 километра от дома.
Следующим этапом расчета количества требуемых фотоэлектрических элементов для электропитания дома является изучение данных:
- Энергоемкости жилья
- Коэффициента инсоляции для конкретной местности
- Номинальной мощности каждого фото модуля
Энергоемкость дома определяется методом экспериментального вычисления потребления электроэнергии в сутки при работе в доме всех электрических приборов.
Обычно номинальная мощность указывается в технических характеристиках модуля. А коэффициент инсоляции, показывающий эффективность будущей работы в определенные сезоны и промежутки времени, можно найти в специальной литературе или Интернете.
Третий этап определения требуемого объема электроэнергии подразумевает ряд математических вычислений, позволяющих рассчитать мощность фотоэлектрической установки.
Если в среднем вы потребляете по 4 кВт часов электроэнергии, номинальная мощность солнечной панели составляет 230 Вт, а коэффициент инсоляции временного промежутка равен: 4часа – полная мощность, 4 часа – 70%, 4часа – 50% мощности, то расчеты выглядят так:
- Среднесуточная выработка энергии каждой панели равна 230 Вт * 4 + 161*4+115*4= 2024 Вт*ч.
- Количество требуемых панелей для удовлетворения всех нужд по электропитанию жилища равен 4000 Вт*ч, т.е. 2 модуля, = 4048 Вт*ч.
Если объект планируется использовать круглогодично, то тут в основном, используются дополнительные источники энергии. Это связанно с тем, что в зимнее время инсоляция солнечной энергии в средней полосе России может быть в 20-ть раз меньше, чем летом. При этом, увеличивая количество панелей в 20-ть раз, столкнемся с трудностями размещения такого количества панелей, увеличенной стоимостью и большим избытком энергии летом. Есть исключения по разнице солнечной инсоляции летом и зимой, например Восточная Сибирь, Алтайский Край, Магаданская область, где солнечных дней в зимнее время сравнимо с летними днями. Тем не менее, дополнительный или резервный источник электроэнергии никогда не помешает. В качестве дополнительного источника электроэнергии используется ветрогенератор. А в качестве резервного источника электроэнергии – бензиновый, газовый или дизель генератор, который при недостатке инсоляции работает всего 3-4 часа.
Поэтому при расчетах нужно отталкиваться от показателей солнечной инсоляции весной, летом или осенью. Недостающая электроэнергия компенсируется дополнительным или резервным источником электроэнергии.
Далее нужно рассчитать необходимый тип и количество батарей аккумулятора. Они нужны как накопители в случае отсутствия солнца и для компенсации пусковых мощностей электроприборов.
Самый популярный тип аккумуляторов – это «гелевые». У них привлекательная цена и высокий КПД 95%. До 800 зарядов и разрядов, при величине их разряда не более 70 %. И температура эксплуатации не должна быть менее +5 градусов Цельсия. Не соблюдение этих параметров выведет из строя гелевые аккумуляторы в течении года. При собледении всех норм эксплуатации, гелевые аккумуляторы прослужат больше, чем три года.
В нашем случае расчет емкости выглядит следующим образом: 4000 Вт*ч + 70 % +5% = 7000 Вт*ч. Емкость аккумуляторов мы используем только в темное время суток, примерно 12 часов, (12/24=0,5).
Общая емкость батарей в 12В составит 0,5 *7000 Вт*ч/12 Вольт = (не менее ) 291 А*ч. Этот показатель станет исходным при выборе количества «гелевых» аккумуляторов.
Второй по популярности тип аккумуляторов – щелочные Никель-Кадмиевые. Цена чуть больше гелевых. Не менее 5000 зарядов и разрядов. КПД 85%, габариты – больше чем гелевые в два раза. Нуждаются в периодическом обслуживании, раз в 6-12 месяцев – доливать воды в каждую банку.
Никель-Кадмиевые аккумуляторы предподчительнее всех других. Автономные станции больших мощностей все стационарные, для больших размеров аккумуляторов всегда место найдется. Никель-кадмиевые аккумуляторы не боятся лютых морозов, поэтому само оборудование можно размещать на улице. Пять лет заводской гарантии и не менее 5000 полных разрядов и зарядов. А частичные разряды не влияют на срок службы. Эти аккумуляторы можно разряжать на все 100%, температура эксплуатации от -40 до +50 градусов Цельсия. Если во время не дольете воду, то бакна аккумулятора просто перестает работать, а после долива воды и тренировки, продолжает так же работать как и раньше.
Расчет для Никель-Кадмиевых аккумуляторов выглядит следующим образом: : 4000 Вт*ч + 15% = 4600 Вт*ч. Емкость аккумуляторов мы используем только в темное время суток, примерно 12 часов, (12/24=0,5).
Общая емкость батарей в 12В составит 0,5 *4600 Вт*ч/12 В = (не менее ) 192 А*ч. Этот показатель станет исходным при выборе количества Никель-Кадмиевых аккумуляторов.
В Минстрое хотят снизить норму инсоляции и строить дома ближе друг к другу
В Минстрое хотят внести поправки в СП 367 относительно освещенности жилых многоэтажных домов, что позволит строить дома немного выше и на меньшем расстоянии друг от друга. Планируется увеличить коэффициент инсоляции и внести изменения в методику расчета отраженного света от соседних домов с фасадом из керамогранита, фасадных красок и панелей.
Кроме того будет обсуждаться возможность использования светоотражающих стекол в остеклении дома и многофункционального покрытия на них, которое способно задерживать свет внутри помещения.
Благодаря такому остеклению появится возможность расходовать меньше ресурсов для отопления и кондиционирования дома. К тому же в поправки будет внесена новая методика проектирования внешних элементов (лоджии, балконы, козырьки), которые непосредственно воздействуют на освещенность в здании.
Игорь Шмаров, главный научный сотрудник НИИСФ РААСН, отметил, что ранее застройщик увеличивал высоту жилого дома на 1-2 этажа без применения светоотражающих материалов при облицовке фасада. Вследствие чего уровень инсоляции не соответствовал норме. Поэтому проект не проходил экспертизу.
Преимущества использования светоотражающих материалов:
- застройщики получают возможность на законных основаниях строить на один-полтора этажа выше;
- высвобождение дополнительных площадей для организации и строительства социально необходимых объектов, улучшения качества городской инфраструктуры;
- количество многоэтажных домов в городе можно увеличить до 15%;
- подводка инженерных систем потребует меньшего объема ресурсов;
- снизится стоимость квадратного метра.
Замминистра строительства и ЖКХ Д.Волков сообщил, что наступил тот период, когда необходимо внедрить и использовать новые методы и данные во время проектирования жилых многоэтажек. Чтобы оптимизировать функциональные зоны и общественные площади, требуется брать во внимание показатель отражения света для составления нового коэффициента освещенности.
Новые правила, внесенные в СП 367, помогут повысить комфорт общественных пространств и современного городского жилья. Использование специальных материалов для остекления и фасада зданий обеспечат более высокий уровень экономической и энергосберегающей эффективности жилых объектов.
Как в Госдуме относятся к уменьшению расстояния между жилыми домами и увеличению этажности
Первый заместитель председателя комитета Госдумы по госстроительству и законодательству М.Емельянов заявил, что они не намерены поддерживать идею Минстроя.
Емельянов уверен, что нововведения направлены на удовлетворение интересов застройщиков, но никак не граждан. В Москве и большинстве регионов России солнца и без того не хватает, вследствие чего — низкий уровень инсоляции. Более плотная застройка уменьшит ее показатель еще на несколько значений, солнечные лучи и вовсе перестанут попадать людям в квартиры.
Ясно одно — благодаря пересмотру норм расчета освещенности у застройщиков будет больше земли для новых проектов. Однако подобные правила не направлены на удовлетворение потребностей граждан в достаточном уровне инсоляции.
Последствия новых правил для застройщиков
Многие уверены, что благодаря нормам инсоляции есть контроль над застройщиками. И если нормы снизить, то в столице и регионах начнется хаотичная застройка жилыми домами “плечом к плечу”, где люди из соседних домов будут пожимать друг другу руки.
Кроме норм инсоляции у застройщиков есть еще ряд других требований к проектам, поэтому вольности в их деятельности не приходится ожидать. Каждый девелопер знает, что если не учитывать общую концепцию градостроительного плана, зону для обеспечения социальной инфраструктурой, квартиры просто никто не будет покупать.
Возможно количество небоскребов заметно вырастет, плотность застройки увеличится, что не совпадает с концепцией создания комфортного проживания в городе. Однако стоит помнить, что в Москве есть верхний предел высоты жилых домов — 75 метров, что составляет 23-25 этажей.
Застройщикам элитных проектов с точечной локацией будет сложно вписать одиночный проект в уже сложившуюся среду. Напомним, что большинство клубных домов относятся к апартаментам, где действует упрощенная норма к инсоляции объекта.
Если предложение Минстроя одобрят, то это не значит, что застройщики будут строить где угодно и сколько угодно. Застройщики смогут сократить время проектирования жилых комплексов и реализовывать новые планировочные решения.
Покупателям также не стоит опасаться. Уровень инсоляции может увеличиться за счет применения новых светоотражающих материалов в облицовке фасадов и остеклении домов с многофункциональным покрытием.
Минстрой намерен увеличить этажность домов с соблюдением норм инсоляции
https://realty.ria.ru/20201119/minstroy-1585325592.html
Минстрой намерен увеличить этажность домов с соблюдением норм инсоляции
Минстрой намерен увеличить этажность домов с соблюдением норм инсоляции — Недвижимость РИА Новости, 19.11.2020
Минстрой намерен увеличить этажность домов с соблюдением норм инсоляции
Минстрой России готовит нормативные изменения, которые позволят увеличить этажность проектов зданий с соблюдением норм естественного освещения, говорится в… Недвижимость РИА Новости, 19.11.2020
2020-11-19T12:41
2020-11-19T12:41
2020-11-19T13:22
министерство строительства и жилищно-коммунального хозяйства рф (минстрой россии)
жилье
строительство
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21.img.ria.ru/images/07e4/07/1f/1575208372_0:160:3072:1888_1920x0_80_0_0_f12385e91f2ead1c3cdcc91f7571d090.jpg
МОСКВА, 19 ноя — РИА Недвижимость. Минстрой России готовит нормативные изменения, которые позволят увеличить этажность проектов зданий с соблюдением норм естественного освещения, говорится в сообщении на сайте ведомства.Министерство при участии научного сообщества готовит проект изменений в СП 367 «Здания жилые и общественные. Правила проектирования естественного и совмещенного освещения». В проект документа включена обновленная инженерная методика расчета отраженной составляющей естественной освещенности от противостоящих зданий с белыми и светлыми фасадными материалами (керамогранит, фасадные панели, фасадные краски), имеющими повышенные (до 0,80) коэффициенты отражения света.Учет возможностей фасадных материалов с повышенными светоотражающими свойствами в проекте документа позволяет увеличивать этажность на 1-1,5 этажа и плотность городской застройки (в пределах 15%). При этом возможно сокращение стоимости единицы площади помещений, говорится в нем.Как добавляется в сообщении, документ также будет учитывать специфику применения стекол с энергосберегающим, солнцезащитным и многофункциональными покрытиями, имеющими пониженный коэффициент пропускания света.
Недвижимость РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2020
Недвижимость РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
Новости
ru-RU
https://realty.ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
Недвижимость РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
https://cdnn21.img.ria.ru/images/07e4/07/1f/1575208372_171:0:2902:2048_1920x0_80_0_0_5cbf747930371df417e73fc6f45e0d5c.jpgНедвижимость РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
Недвижимость РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
министерство строительства и жилищно-коммунального хозяйства рф (минстрой россии), жилье, строительство
МОСКВА, 19 ноя — РИА Недвижимость. Минстрой России готовит нормативные изменения, которые позволят увеличить этажность проектов зданий с соблюдением норм естественного освещения, говорится в сообщении на сайте ведомства.Министерство при участии научного сообщества готовит проект изменений в СП 367 «Здания жилые и общественные. Правила проектирования естественного и совмещенного освещения». В проект документа включена обновленная инженерная методика расчета отраженной составляющей естественной освещенности от противостоящих зданий с белыми и светлыми фасадными материалами (керамогранит, фасадные панели, фасадные краски), имеющими повышенные (до 0,80) коэффициенты отражения света.
«Коэффициент естественной освещенности для жилых помещений равен 0,5. Если застройщики ранее без применения данных фасадных материалов «поднимали» строение на два этажа, то коэффициент не удовлетворял требованиям нормы, и проект объекта капитального строительства не проходил экспертизу», – отмечается в сообщении.
Учет возможностей фасадных материалов с повышенными светоотражающими свойствами в проекте документа позволяет увеличивать этажность на 1-1,5 этажа и плотность городской застройки (в пределах 15%). При этом возможно сокращение стоимости единицы площади помещений, говорится в нем.
Как добавляется в сообщении, документ также будет учитывать специфику применения стекол с энергосберегающим, солнцезащитным и многофункциональными покрытиями, имеющими пониженный коэффициент пропускания света.
Статьи
РОЛЬ СОЛНЕЧНОЙ РАДИАЦИИ В ФОРМИРОВАНИИ ТЕПЛО-ВЕТРОВОГО РЕЖИМА МЕЖДОМОВОГО ПРОСТРАНСТВА
Вестник МГСУ 3/2012- Гиясов Ботир Иминжонович - Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ) кандидат технических наук, доцент, заведующий кафедрой архитектурно-строительного проектирования, Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ), 129337, г. Москва, Ярославское шоссе, д. 26; Этот e-mail адрес защищен от спам-ботов, для его просмотра у Вас должен быть включен Javascript .
Страницы 12 — 15
В результате анализа теплофизических процессов междомового пространства с выявлением механизма конвективных движений у поверхностей отмечается значительная роль солнечной радиации в регулировании тепло-ветрового режима, определяемая условием инсоляции поверхностей и степенью преобразования им тепла. Интенсивное воздействие солнечной радиации на поверхность ограждающих конструкций зданий способствует возникновению конвективных потоков, которые формируют тепло-ветровой режим дворов.
DOI: 10.22227/1997-0935.2012.3.12 — 15
Библиографический список- Гиясов А. Исследование тепло-ветровых процессов на модели жилой застройки городов с жарко-штилевым условием климата // Известия ВУЗов. Строительство и архитектура. 1989. № 6. С. 43-47.
- Абдуллоев М. Аэродинамические характеристики жилых зданий в условиях сложного рельефа : автореф. дисс. … канд. техн. наук. М., 1984. 24 с.
- Гиясов Б.И. Влияние жарко-штилевого климата на ограждающие конструкции и микроклимат жилых зданий : автореф. дисс. … канд. техн. наук. М., 2000. 24 с.
- Абрамович Г.Н. Теория турбулентных струй. М. : Физматгиз, 1960. 375 с.
- Баум В.А., Бабаев Ч. Исследование поглощения солнечной радиации различными материалами // Гелиотехника. 1966. № 3. С. 54-61.
Cкачать на языке оригинала
БЕЗОПАСНОСТЬ СВЕТОКЛИМАТИЧЕСКОЙ СРЕДЫ ЗДАНИЙ ПРИ СТРОИТЕЛЬСТВЕ И РЕКОНСТРУКЦИИ В УСЛОВИЯХ ПЛОТНОЙ ГОРОДСКОЙ ЗАСТРОЙКИ
Вестник МГСУ 8/2017 Том 12- Римшин Владимир Иванович - Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ) доктор технических наук, член-корреспондент РААСН, профессор кафедры жилищно-коммунального комплекса, Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ), 129337, г. Москва, Ярославское шоссе, д. 26.
- Кузина Екатерина Сергеевна - Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ) магистрант, Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ), 129337, г. Москва, Ярославское шоссе, д. 26.
Страницы 917-923
В статье рассмотрены вопросы обеспечения безопасности светоклиматической среды в условиях плотной городской застройки при строительстве и реконструкции зданий. Приведен пример расчета инсоляции и естественного освещения многоэтажного жилого здания с учетом всех нормативных требований, влияния окружающей застройки, их расположения и габаритов. Выяснено, что естественное освещение и инсоляционный режим помещений рассмотренного многоэтажного жилого дома соответствуют требованиям нормативных документов для естественного освещения и инсоляции жилой застройки, что обеспечит безопасное и комфортное проживание. Приведенный пример расчета можно применять для улучшения инсоляционного режима и естественного освещения в существующей плотной городской застройке с обеспечением всех действующих норм.
DOI: 10.22227/1997-0935.2017.8.917-923
Библиографический список- Курбатов В.Л., Римшин В.И., Шумилова Е.Ю. Практическое пособие производителя работ. Белгород : БГТУ им. Шухова, 2013.
- Слукин В.М., Симакова Е.С. Проблемы естественного освещения помещений в уплотненной городской застройке // Академический вестник УралНИИпроект РААСН. 2010. № 2. С. 56-60.
- Курбатов В.Л., Римшин В.И. Практическое пособие инженера-строителя / под ред. В.И. Римшина. М. : Студент, 2012.
- Нотенко С.Н., Римшин В.И., Ройтман А.Г. и др. Техническая эксплуатация жилых зданий / под ред. В.И. Римшина, А. М. Стражникова. 3-е изд., перераб. и доп. М. : Студент, 2012.
- Римшин В.И., Греджев В.А. Правоведение. Основы законодательства в строительстве. М : Изд-во Ассоциации строительных вузов,. 2015.
- Бондаренко В.М., Римшин В.И. Диссипативная теория силового сопротивления железобетона. М. : Студент, 2015.
- Бондаренко В.М., Римшин В.И. Остаточный ресурс силового сопротивления поврежденного железобетона. // Вестник Отделения строительных наук Российской академии архитектуры и строительных наук. 2005. № 9. С. 119.
- Курбатов В.Л., Римшин В.И., Шумилова Е.Ю. Строительно-техническая экспертиза. Минеральные Воды : КМБ СКФ БГТУ им. В. Г. Шухова, 2015.
- Ларионов Е.А., Римшин В.И., Василькова Н.Т. Энергетический метод оценки устойчивости сжатых железобетонных элементов // Строительная механика инженерных конструкций и сооружений. 2012. № 2. С. 77-81
- Римшин В.И., Греджев В.А. Основы правового регулирования градостроительной деятельности. 2-е изд. перераб. и доп. М. : Студент, 2015.
- Римшин В.И., Греджев В.А. Правовое регулирование городской деятельности и жилищное законодательство. М. : Инфра-М, 2013. (Высшее образование)
- Erofeev V.T., Zavalishin E.V., Rimshin V.I., et al. Frame composites based on soluble glass // Research Gournal of Pharmaceutical, Biological and Chemical Sciences. 2016. Vol. 7. № 3. С. 2506-2517.
- Korotaev S.A., Kalashnikov V.I., Rimshin V.I. et al. The impact of mineral aggregates on the thermal conductivity of cement composites // Ecology, Environment and Conservation. 2016. Vol. 22. № 3. Pp. 1159-1164.
- Antoshkin V.D., Erofeev V.T., Travush V.I., et al. The problem optimization triangular geometric line field // Modern Applied Science. 2015. Vol. 9. № 3. Pp. 46-50.
- Erofeev V.T., Bogatov A.D., Bogatova S.N., et al. Bioresistant building composites on the basis of glass wastes // Biosciences Biotechnology Research Asia. 2015. Vol. 12. № 1. С. 661-669.
- Krishan A., Rimshin V., Markov S., et al. The energy integrity resistance to the destruction of the long-term strength concrete // Procedia Engineering. 2015. Vol. 1. Pp. 211-217.
- Rimshin V.I., Larionov E.A., Erofeyev V.T., Kurbatov V.L. Vibrocreep of concrete with a nonuniform stress state // Life Science Journal. 2014. Т. 11. № 11. Pp. 278-280.
Скачать статью
Увеличить этажность застройки без потерь инсоляции планирует Минстрой
Минстрой России обеспечит возможность увеличения этажности проектов зданий с соблюдением норм естественного освещения, говорится в сообщении Минстроя, готовящего соответствующий проект при участии научного сообщества.«Коэффициент естественной освещенности для жилых помещений равен 0,5 и закреплен в санитарных нормах СанПиН «Гигиенические требования к естественному, искусственному и совмещенному освещению», обязательных к применению. Если застройщики ранее «поднимали» строение на два этажа, то КЕО не удовлетворял требованиям нормы, и проект объекта капитального строительства, соответственно, не проходил экспертизу», – пояснил главный научный сотрудник НИИСФ РААСН, к.т.н. Игорь Шмаров.
Проект предполагает новые подходы в СП 367 «Здания жилые и общественные. Правила проектирования естественного и совмещенного освещения». В документ включена обновленная инженерная методика расчета отраженной составляющей естественной освещенности от противостоящих зданий с белыми и светлыми фасадными материалами (керамогранит, фасадные панели, фасадные краски), имеющими повышенные (до 0,80) коэффициенты отражения света.
В Минстрое говорят, что изменения СП 367 позволяют увеличивать этажность на 1-1,5 этажа и плотность городской застройки (в пределах 15 %), при этом возможно сокращение стоимости единицы площади помещений.
«Это даст возможность высвободить городские площади, которые можно использовать для улучшения инфраструктуры городских территорий. И, кроме того, здесь есть еще один несомненный «плюс» – сокращение затрат на подводку инженерных коммуникаций», – отметил Игорь Шмаров.
Документ также будет учитывать возможность применения фасадного остекления с энергосберегающими стеклами с твердым и мягким низкоэмиссионным, солнцезащитным и многофункциональным покрытием, имеющими пониженный коэффициент пропускания света при удовлетворении требованиям норм естественной освещенности в помещениях проектируемых зданий для выполнения норм естественного освещения в прилегающей застройке.
«Сейчас – очень актуальное время для изыскания имеющихся у нас резервов, реализации потенциалов, которые нам дают наши наукоемкие подразделения. Назрела необходимость дополнения свода правил положениями, которые позволят обеспечить проектные организации самыми новыми методами и данными для расчетов естественного и совмещенного освещения помещений жилых и общественных зданий, в том числе в условиях плотной городской застройки. Учет отраженной составляющей естественного света при определении коэффициента естественной освещенности – перспективный инструмент оптимизации жилых функциональных зон и общественных пространств», – сказал заместитель министра строительства и ЖКХ РФ Дмитрий Волков.
Применение стекол с энергосберегающими покрытиями в остеклении фасадов сокращает расходы на отопление зданий за счет снижения потерь тепла через светопрозрачные конструкции в отапливаемый период года. Также сократятся расходы на кондиционирование воздуха за счет снижения поступления солнечной радиации в помещения в летнее время. Таким образом, за счет внедрения современных материалов дома и в общественных местах для людей может быть создан комфортный микроклимат.
Готовящееся обновление в свод правил также включает новую более гибкую инженерную методику учета влияния архитектурных элементов фасадов зданий (балконов, лоджий, вертикальных и горизонтальных козырьков), учитывающую многообразие архитектурных решений, влияющих на естественную освещенность помещений. Наличия методики будет способствовать повышению архитектурной выразительности городской застройки.
«Подготовленный документ поможет сделать более комфортными общественные пространства и современное городское жилье для граждан, а применение новых материалов позволит повысить энергетическую и экономическую эффективность новых объектов. Во главе угла – здоровье людей и их комфорт», – заключил Дмитрий Волков.
Расчет солнечной инсоляции | PVEducation
На основе уравнения положения солнца на небе в течение года можно рассчитать максимальное количество солнечной инсоляции на поверхности при определенном угле наклона как функцию широты и дня года. Эти расчеты также важны при использовании экспериментальных данных счетчиков солнечного часа. Следующие анимации вычисляют дневную солнечную освещенность, солнечную инсоляцию и количество часов в течение дня, когда светит солнце.Они не включают в себя местные погодные эффекты, поэтому эти теоретические графики не используются при определении размеров системы или прогнозировании работы. Описание каждого графа дается в подписи под ним.
График показывает интенсивность прямого излучения в Вт / м² в течение дня. Это количество энергии, которое получит концентратор слежения при отсутствии облака. Время — местное солнечное время. Установите широту своего местоположения, а затем отрегулируйте ползунок дня, чтобы увидеть, сколько радиации существует для каждого дня в году.Нажмите на график для числовых данных
Средняя дневная солнечная инсоляция как функция широты. Три кривые — это падающая солнечная инсоляция, горизонтальная солнечная инсоляция и солнечная инсоляция на названной поверхности, как определено на странице Module Tilt. Суточная инсоляция численно равна количеству солнечных часов в сутки. Предполагается, что модуль обращен к экватору так, что он обращен на юг в северном полушарии и на север в южном полушарии. Поскольку широта регулируется через ноль, проходя через экватор, модуль смотрит в противоположном направлении.график внезапно меняется на экваторе, поскольку теперь модуль смотрит в противоположном направлении. Нажмите на график для числовых данных
Количество часов, в течение которых солнце светит каждый день, то есть количество часов между восходом и заходом солнца каждый день. На широтах выше 67 ° солнце светит 24 часа в течение части года. Удивительно, но в среднем за год солнце светит в среднем 12 часов в день во всем мире. В северных широтах средняя интенсивность ниже, чем в южных широтах.Нажмите на график для числовых данных
Уравнения для построения вышеуказанных графиков приведены ниже. Эти уравнения рассчитываются по солнечному времени, а не по местному времени. Коррекция между местным солнечным временем и местным временем приведена на странице Положение Солнца.
Количество солнечных часов — это просто время между восходом солнца:
Восход солнца = 12−1150cos − 1 (−sinφsinδcosφcosδ)
и закат:
Закат = 12 + 1150cos − 1 (−sinφsinδcosφcosδ)
Прямая составляющая солнечного излучения определяется по воздушной массе:
ID = 1.353 × 0,7 (AM0,678)
Массу воздуха можно определить по формуле воздушной массы:
AM = 1cosθ
Поглощенное солнечное излучение
Поглощенное солнечное излучение по цвету поверхности
Поглощенная солнечная энергия зависит от цвета поверхности:
| Цвет поверхности | Коэффициент поглощения — доля поглощенного падающего излучения (приблизительно) |
|---|---|
| Белый гладкие поверхности | 0,25 — 0,40 |
| От серого до темно-серого | 0.40 — 0,50 |
| Зеленый, красный и коричневый | 0,50 — 0,70 |
| От темно-коричневого до синего | 0,70 — 0,80 |
| От темно-синего до черного | 0,80 — 0,90 |
Поглощенное солнечное излучение Излучение материала
| Вещество | Фактор поглощения — Доля поглощенного падающего излучения |
|---|---|
| Алюминий, полированный | 0,30 |
| Алюминий краска | 0.20 |
| Алюминий анодированный | 0,15 |
| Кирпич глазурованный | 0,35 |
| Кирпич обыкновенный светлый красный | 0,55 |
| Кирпич обыкновенный красный | 0,68 |
| Кирпич, красная проволока | 0,52 |
| Кирпич синий | 0,89 |
| Пробка | 0,45 |
| Известняк светлый | 0.35 |
| Известняк, темный | 0,50 |
| Линолеум, красно-коричневый | 0,84 |
| Песчаник, светло-серый | 0,62 |
| Песчаник, красный | 0,73 |
| Мрамор, белый | 0,44 |
| Мягкая резина, серый | 0,65 |
| Мрамор, темный | 0,66 |
| Гранит, красноватый | 0.55 |
| Оксид магния, испаренный | 0,08 |
| Графит | 0,84 |
| Фарфор | 0,50 |
| Сталь, стекловидная эмаль, зеленая | 0,76 |
| Сталь, стекловидная эмаль темно-красная | 0,81 |
| Сталь, стекловидная эмаль синяя | 0,80 |
| Железо оцинкованное новое | 0,64 |
| Оцинкованное грязное | 0.92 |
| Чугун, оцинкованный, побеленный | 0,22 |
| Бетон | 0,60 |
| Медь полированная | 0,18 |
| Медь потускненная | 0,64 |
| Свинец, старый | 0,79 |
| Асбестоцемент, старая черепица | 0,83 |
| Асбестоцемент, красная черепица | 0,69 |
| Асбестовый шифер | 0.81 |
| Покрытие из асфальта, новое | 0,91 |
| Покрытие из асфальта, старое | 0,82 |
| Кровельный лист, покрытый битумом, коричневый | 0,87 |
| Шифер, серо-голубой | 0,87 |
| Плитка красная глина | 0,64 |
| Плитка бетонная бесцветная | 0,65 |
| Плитка бетонная черная | 0,91 |
| Стекловидная эмаль, белая | 0.39 |
| Белая голландская плитка | 0,18 |
Обзор викторины
Количество солнечной радиации, отраженной от поверхности, называется:
- а. инсоляция
б. альбедо
c. диффузионность
d.излучательная способность
е. коэффициент цвета
Парниковые газы наиболее эффективно поглощают энергию ________ длин волн.
- а. видимый
б. ультрафиолетовый
c. инфракрасный
d.микроволновая печь
е. короче
Планетарное альбедо Земли составляет около _____ процентов.
- а. 10
б. 17
c. 33
d.45
е. 50
Количество поступающей солнечной радиации, которая достигает поверхности Земли, называется
.- а. инсоляция
б. небесное излучение
c. альбедо
d.чистая радиация
Большая часть тепла Земли уходит в диапазоне длин волн от 8,5 до 13 микрометров, который также называется:
- а. разрыв
б. атмосферное окно
c. дверь атмосферы
d.озоновая дыра
Солнечная постоянная
- а. полная энергия, излучаемая солнцем
б. полная солнечная энергия, поглощаемая поверхностью Земли
c. полная солнечная энергия, достигающая верха атмосферы
d.ни один из этих
Переизлучение Земли обратно в космос происходит в основном в ____ длинах волн.
- а. видимый
б. ультрафиолетовый
c. инфракрасный
d. микроволновая печь
е.радио
Если бы не парниковый эффект, средняя температура на Земле была бы около
.- а. 0 ° C
б. 0 ° F
c. 32 ° F
d. 50 ° F
е.60 ° F
Для достижения идеального равновесия чистая радиация Земли должна быть:
- а. -10% солнечной постоянной
б. 0% солнечной постоянной
c. 10% солнечной постоянной
d.25% солнечной постоянной
Глобальная чистая радиация составляет:
- а. положительный в тропиках, отрицательный в полярных регионах
б. положительный в полярных регионах, отрицательный в тропиках
c. положительный на всех широтах
d.ноль на всех широтах
Когда тепло передается между молекулами, находящимися в контакте друг с другом, это называется:
- а. конвекция
б. проводимость
c. радиация
d.явное тепло
Разница между поглощенной и испускаемой радиацией на поверхности Земли называется _____.
- а. полученное тепло
б. инсоляция
c. чистая радиация
d.остаточная радиация
Самый эффективный парниковый газ при поглощении тепла:
- а. углекислый газ
б. метан
c. водяной пар
d. ХФУ
Солнечное излучение на задней поверхности двусторонних солнечных модулей: подход к моделированию
Испытательный полигон и модуль
Испытательный полигон находится на крыше физического факультета METU, Анкара (Центральная Анатолия).Климат полигона жаркий и умеренно-полузасушливый теплый 10 . Широта Анкары составляет 39,9 ° с.ш., а долгота — 32,8 ° в.д. Годовое количество осадков за последние 30 лет составляет 388,1 мм. Среднемесячная температура около 12 ° C. В июле и августе максимальная средняя температура повышается до 30 ° C, а в январе минимальная средняя температура снижается до -3 ° C (Государственная метеорологическая служба Турции; https://www.mgm.gov.tr).
Тестовая платформа имеет 16 испытательных стендов для мониторинга производительности фотоэлектрических модулей.Эти стенды удобны для различных типов и рамных конструкций фотоэлектрических модулей. Помещение на крыше физического факультета в кампусе METU показано ниже на рис. 1, а двухсторонний модуль, протестированный в этом исследовании, обозначен красными линиями. Испытательная платформа имеет угол наклона 32 °, а угол наклона фотоэлектрических систем такой же, как и у испытательных стендов.
Рис. 1( a ) Открытый испытательный стенд в GUNAM, METU. Красный квадрат указывает на тестируемый двусторонний модуль. ( b ) Представление всех компонентов в испытательном стенде.
На открытой тестовой платформе Daystar Multi Tracer 5 измеряет рабочие параметры фотоэлектрических модулей и температуру модулей с помощью термопар, одна из которых подключена к двустороннему модулю в данной работе. Есть два пиранометра, которые мы используем для измерения горизонтального и плоского излучения. В настоящей работе мы использовали эти два пиранометра. Мы также измеряем солнечное излучение на горизонтальной поверхности с помощью метеостанции Davis. Тестовое устройство Daystar может измерять производительность каждого модуля, используя как средние, так и мгновенные параметры с 10-минутным интервалом времени.В таблице 1 приведены измеренные параметры. Данные легко доступны с использованием протокола FTP.
Таблица 1 Сводка параметров, которые тестовое устройство измеряет для оценки производительности фотоэлектрических модулей.Мы записываем все метеорологические данные с 2015 года. Метеостанции могут измерять количество осадков (мм), давление (миллибар), температуру окружающей среды (° C), относительную влажность (%), горизонтальную общую солнечную радиацию (Вт / м 2) ), доза УФ-излучения (MED), скорость ветра (м / с) и направление (°).В этом исследовании мы использовали один двусторонний модуль PV. В таблице 2 приведены характеристики модуля. Длина и ширина модуля составляют 1,61 м и 1,0 м соответственно. Самая низкая точка модуля находится на 0,5 м выше серого бетонного грунта с альбедо 0,2.
Таблица 2 Сводка свойств двустороннего модуля PV.Мы сконструировали три различные установки для наблюдения за влиянием возвышения на землю, отраженное излучение, принимаемое задней стороной двустороннего фотоэлектрического модуля.Поместив два пиранометра на задней стороне двустороннего фотоэлектрического модуля на трех разных уровнях высоты, на двух уровнях одновременно, мы измерили освещенность задней стороны соответственно. На рис. 2 показаны три конфигурации пиранометров на задней стороне двустороннего фотоэлектрического модуля. Данные включают три типичных дня для трех конфигураций. Первая конфигурация включает один пиранометр посередине, а другой внизу: 0,84 и 0,50 м над землей. Для второй конфигурации мы разместили пиранометр снизу вверх 0.50 и 1,16 м над землей. В качестве заключительного шага для третьей конфигурации мы удалили центральную и поместили ее внизу: 1,16 и 0,50 м над землей.
Рисунок 2( a ) Первая конфигурация с одним пиранометром находится внизу сзади (0,50 м), а другой — посередине сзади (0,84 м). ( b ) Вторая конфигурация с одним пиранометром находится вверху-спине (1,16 м), а другой — посередине сзади (0,84 м). ( c ) Третья конфигурация с одним пиранометром находится внизу сзади (0.50 м), а второй — вверху-спине (1,16 м).
Введение в методологию
Представленная здесь модель является модифицированной версией стандартной модели неба, которая представляет собой изотропную диффузную модель, полученную Лю и Джорданом 11 . Изотропная диффузная модель предполагает, что все диффузное излучение изотропно, что означает, что интенсивность диффузного излучения одинакова по всему небесному куполу. Облучение наклонного фотоэлектрического модуля, состоящего из трех компонентов; луч, изотропный диффузный и диффузно отраженный от земли.Облучение пучком — это прямое излучение, исходящее от Солнца без рассеяния в атмосфере. Диффузное излучение — это излучение, полученное от Солнца после рассеяния атмосферой, и его труднее оценить, поскольку оно зависит от облачности и чистоты атмосферы 7 . Последний компонент изотропной модели — это отраженное от земли излучение от поверхности земли и от любых других окружающих предметов. Комбинируя три компонента, предложенные Лю и Джордан 9 , солнечное излучение на наклонной поверхности можно найти следующим образом:
$$ I_ {t} = I_ {b} R_ {b} + I_ {d} \ left ({\ frac {1 + cos \ beta} {2}} \ right) + I \ rho_ {g} \ left ({\ frac {1 — cos \ beta} {2}} \ right), $$
(1)
где \ (I_ {b} \) — это почасовое облучение пучком на горизонтальной поверхности, а \ (R_ {b} \) — это отношение почасового облучения пучком на наклонной поверхности к таковому на горизонтальной поверхности 12 .\ (R_ {b} \) отличается для задней поверхности и в нашей методике определяется симметрией пути солнечного излучения относительно течения времени. Второй компонент уравнения. (1) относится к диффузному облучению на наклонной поверхности, где \ (I_ {d} \) — ежечасное диффузное облучение на горизонтальной поверхности, \ (\ beta \) — угол наклона модуля, а \ (\ left ({\ frac {1 + cos \ beta} {2}} \ right) \) — коэффициент обзора от коллектора до неба 13 . Последний компонент — это вклад отраженного от земли, где I — глобальное солнечное излучение на горизонтальной поверхности, \ (\ rho_ {g} \) — коэффициент отражения земли (альбедо), а третий множитель — это коэффициент обзора от коллектора до земля.
Описание модели
В этой работе мы модифицировали изотропную диффузную модель Лю и Джордана для оценки излучения тыльной стороны. Первая модификация модели — угол наклона, вместо β в качестве угла наклона берется дополнительный β . Причина этой модификации заключается в том, что задняя сторона рассматривается как передняя, поэтому угол наклона задней стороны является дополнением β (π– β ). Эта поправка вносит вклад в компонент излучения, отраженного от земли (третий компонент в уравнении.1) выше, чем в исходной версии, как и ожидалось. На рисунке 3 представлены компоненты солнечного излучения, падающего на двусторонний фотоэлектрический модуль.
Рисунок 3Компоненты солнечного излучения, падающего на двусторонний фотоэлектрический модуль.
Вторая модификация — это изменение коэффициента излучения пучка на тыльной стороне двустороннего фотоэлектрического модуля. Угол падения и коэффициент излучения пучка на лицевую поверхность рассчитывались согласно [5]. 9 , который включает такие параметры, как широта, склонение, угол наклона, часовой угол и азимутальный угол поверхности.Для часов, когда угол падения больше 90 °, что означает, что Солнце находится на задней поверхности, следующие значения R b, front принимаются в качестве отношения излучения луча на задней поверхности R б, задний . Вклад луча на тыльную поверхность обусловлен симметрией пути Солнца. На задней поверхности присутствует только луч света для часов восхода и заката. Примерный набор расчета R b, назад для произвольного дня приведен ниже в таблице 3.Первые и последние два числа соответствуют часам, когда Солнце светит на тыльную сторону. Для этих часов числа в последнем столбце — это числа, которые мы используем для R b, back , которые размещены с учетом вышеупомянутого соображения симметрии.
Таблица 3 R b, назад расчет между восходом и заходом солнца для произвольного дня.В этом исследовании все расчеты производятся для часов между восходом и заходом солнца.Отрицательные значения R b , передний были приняты за ноль.
Последнее изменение связано с соотношением между отраженным излучением от земли и высотой различных частей задней стороны модуля 14 . Поскольку разные части получают разное количество отраженного от земли излучения, можно использовать поправочный коэффициент для заднего освещения.
$$ I_ {t, назад} = I_ {b} R_ {b, back} + I_ {d} \ left ({\ frac {1 — cos \ beta} {2}} \ right) + I \ rho f \ left (h \ right) \ left ({\ frac {1 + cos \ beta} {2}} \ right).$$
(2)
Чтобы учесть разницу между этими значениями облучения, можно использовать функцию распределения высоты \ (f \ left (h \ right), \), из которой можно вывести среднее значение поправочного коэффициента. Эта функция должна быть интегрирована в интервале 0,5–1,16 м (минимальная и максимальная высота модуля от земли соответственно). Можно использовать различные функции распределения для нахождения среднего поправочного коэффициента при условии, что параметр функции определяется с использованием имеющихся параметров системы.{l / 1.21}} \ right) dl, $$
(5)
, что дает:
$$ F \ left (l \ right) = 0,33. $$
Здесь мы предположили, что средний поправочный коэффициент нормализован из максимально возможного поправочного значения 1. Таким образом, для двустороннего солнечного модуль, мы обнаружили, что средний поправочный коэффициент \ (f \ left (h \ right) = 0,33 \). Используя это значение в формуле. (2), мы достигли модельного расчета солнечного излучения, падающего на заднюю поверхность, как:
$$ I_ {t, back} = I_ {b} R_ {b, back} + I_ {d} \ left ({\ frac {1 — cos \ beta} {2}} \ right) + 0.33I \ rho \ left ({\ frac {1 + cos \ beta} {2}} \ right). $$
(6)
Расчет доходности фотоэлектрических модулей на двух сторонах
Для проведения технико-экономического обоснования крайне важно оценить доходность фотоэлектрического модуля или массива. Многие инструменты позволяют нам рассчитать выход энергии коммерческого (однофасциального) фотоэлектрического модуля. В этом исследовании мы использовали модифицированную версию PVForm 15,16 . {5}, $$
(8)
$$ I_ {tr} = I_ {poa} — \ left ({1 — f} \ right) I_ {b} {\ cos} \ left (\ theta \ right), $$
(9)
где \ (b_ {0}, b_ {1}, b_ {2}, b_ {3}, b_ {4}, b_ {5} \) — коэффициенты полинома покрытия модуля и равны 1.0, — 2.438E − 3, 3.103E − 4, 1.246E − 5, 2.112E − 7, — 1.359E − 9 соответственно. \ (I_ {tr} \) — передаваемая освещенность, \ (I_ {b} \) — составляющая луча, а \ (\ theta {} \) — угол падения.
Мы интегрировали тепловую модель, разработанную Fuentes 19 , в представленную модель, чтобы определить температуру ячейки. Для расчета рабочей температуры ячейки в соответствии с моделью использовались общая освещенность в плоскости решетки, скорость ветра и температура по сухому термометру (или окружающей среде). Модель рассчитывает выходную мощность постоянного тока, регулируя эффективность массива для значений излучения менее 125 Вт / м 2 .\ circ {\ text {C}} \) и \ (P_ {dc0} \) — номинальный ток постоянного тока на паспортной табличке.
Есть несколько модификаций, которые мы сделали для оценки двусторонней PV доходности. Во-первых, значения склонения и угла падения вычисляются с использованием более точных формул. (2) и (4) соответственно. Во-вторых, мы вычислили \ (I_ {poa} \) для передней и задней поверхностей (а именно, \ (I_ {t} \) и \ (I_ {t, back} \) в нашем контексте), используя уравнение. (1) и полученное уравнение. (6) настоящей работы, а затем вычисляются \ (I_ {tr} \) и \ (I_ {tr, back} \).Для расчета \ (I_ {tr, back} \) вместо фильтрации данных для углов падения мы применили поправку AOI для часов, когда на заднюю поверхность падает пучок излучения, что означает, что \ (R_ {b , back} \) больше нуля. Найдя выходную мощность постоянного тока для обеих поверхностей, мы сложили их, чтобы найти общую выходную мощность постоянного тока.
$$ P_ {dc, total} = P_ {dc, front} + P_ {dc, back}. $$
(12)
PV Совместное моделирование производительности | Perez Sky Diffuse Модель
В то время как модель диффузного неба, представленная до этого момента, явно разделяла изотропную, околосолнечную и горизонтальную составляющие, Перес разработал более сложную модель, которая опирается на набор эмпирических коэффициентов для каждого члена.
Базовая форма модели:
,
, где и — сложные эмпирически подобранные функции, описывающие околосолнечную яркость и яркость горизонта соответственно.
, и.
,
Коэффициенты определены для конкретных ячеек четкости (), которая определяется как:
,
где — прямая нормальная освещенность и постоянная величина, равная для углов в радианах или для углов в градусах.
где — абсолютная масса воздуха, а — внеземное излучение.
Perez опубликовал ряд различных версий коэффициентов, приспособленных к различным наборам данных [2, 3, 4]. В таблице 1 приведены значения коэффициента освещенности, опубликованные в [3]. Бункер относится к ячейкам с прозрачностью, определенной в Таблице 2.
Таблица 1. Коэффициенты модели Переса для освещенности (из Таблицы 6 в [3])
| бункер | f11 | f12 | f13 | f21 | f22 | f23 |
| 1 | -0.008 | 0,588 | -0,062 | -0,06 | 0,072 | -0,022 |
| 2 | 0,13 | 0,683 | -0,151 | -0,019 | 0,066 | -0,029 |
| 3 | 0,33 | 0,487 | -0,221 | 0,055 | -0,064 | -0,026 |
| 4 | 0,568 | 0.187 | -0,295 | 0,109 | -0,152 | -0,014 |
| 5 | 0,873 | -0,392 | -0,362 | 0,226 | -0,462 | 0,001 |
| 6 | 1,132 | -1,237 | -0,412 | 0,288 | -0,823 | 0,056 |
| 7 | 1,06 | -1.6 | -0,359 | 0,264 | -1,127 | 0,131 |
| 8 | 0,678 | -0,327 | -0,25 | 0,156 | -1,377 | 0,251 |
Таблица 2. Границы четкости неба (из Таблицы 1 в [3])
| бункер | Нижняя граница | Верхняя граница |
| 1 Пасмурно | 1 | 1.065 |
| 2 | 1.065 | 1,230 |
| 3 | 1,230 | 1,500 |
| 4 | 1,500 | 1,950 |
| 5 | 1,950 | 2,800 |
| 6 | 2,800 | 4.500 |
| 7 | 4.500 | 6.200 |
| 8 Прозрачный | 6.200 | – |
Список литературы
- [1] Loutzenhiser P.G. et. al. «Эмпирическая проверка моделей для расчета солнечного излучения на наклонных поверхностях для моделирования энергии зданий» 2007, Solar Energy vol. 81. pp. 254-267 .
- [2] Перес, Р., Силс, Р., Инейхен, П., Стюарт, Р., Меникуччи, Д., 1987. Новая упрощенная версия модели диффузной освещенности Переса для наклонных поверхностей.Солнечная энергия 39 (3), 221–232.
- [3] Перес, Р., Инейхен, П., Силс, Р., Михальский, Дж., Стюарт, Р., 1990. Моделирование доступности дневного света и компонентов освещенности от прямого и глобального излучения. Солнечная энергия 44 (5), 271–289.
- [4] Perez, R. et. al 1988. «Разработка и проверка модели диффузного излучения Переса». SAND88-7030
Материалы предоставлены Sandia National Laboratories
Расчет диффузной доли глобального горизонтального солнечного излучения: сравнение моделей
Sol Energy.2012 июн; 86 (6): 1796–1802.
Кафедра строительной физики и экологии зданий, Венский технологический университет, Вена, Австрия
Поступила в редакцию 3 августа 2011 г .; Пересмотрено 11 марта 2012 г .; Принято к печати 12 марта 2012 г.
Эта статья цитируется в других статьях в PMC.Основные моменты
► Сравнение восьми различных моделей для оценки диффузной доли излучения. ► Для более подробного анализа выбраны три более эффективные модели. ► Коэффициенты моделей модифицированы с учетом данных Вены.► Некоторые модели обеспечивают относительно надежные оценки диффузных фракций. ► Процедура калибровки лишь незначительно улучшает характеристики моделей.
Ключевые слова: Диффузное излучение, Солнечное излучение, Модели диффузной фракции, Измерения
Реферат
Для прогнозирования использования энергии зданиями или ожидаемой выгоды от интегрированных в здания систем солнечной энергии информация как о прямой, так и о рассеянной составляющей солнечного излучения необходимо.Однако доступные измеренные данные обычно ограничиваются глобальной горизонтальной освещенностью. Таким образом, в прошлом было много попыток разработать алгоритмы для определения диффузной доли солнечного излучения. В этом контексте в настоящей статье сравниваются восемь моделей для оценки диффузной доли излучения на основе базы данных измеренной освещенности из Вены, Австрия. Эти модели обычно включают математические формулировки с несколькими коэффициентами, значения которых обычно действительны для конкретного местоположения.После первого сравнения этих восьми моделей для более подробного анализа были выбраны три более эффективные модели. Таким образом, коэффициенты моделей были изменены с учетом данных Вены. Результаты показывают, что некоторые модели могут обеспечить относительно надежные оценки диффузных фракций глобальной освещенности. Процедура калибровки могла лишь незначительно улучшить характеристики моделей.
Номенклатура
- I
- общая горизонтальная освещенность (Вт · м −2 )
- I d
- диффузная горизонтальная освещенность (Вт · м −2 I 904 904)
- внеземное солнечное излучение (Вт · м −2 )
- I sc
- внеземное постоянное солнечное излучение (1367 Вт · м −2 )
- I
04 прямое излучение4 горизонтальная поверхность (Вт м −2 ) - k t
- индекс прозрачности (безразмерный)
- k d
- диффузная фракция (безразмерный)
высота- солнце (°)
- T a
- температура наружного воздуха (° C)
- ϕ
- относительная влажность (%)
- 9 1059 G t
- среднемесячная глобальная радиация на горизонтальной поверхности (Вт · м −2 )
- ζ
- угол наклона поверхности, измеренный от горизонтали (°)
- м a
- воздушная масса (безразмерная) при фактическом давлении
- м r
- воздушная масса (безразмерная) при стандартном давлении (1013.25 мбар)
- p
- местное давление воздуха (мбар)
- N
- номер дня в году (No.)
- n
- количество данных
- θ z
- зенитный угол (°)
1. Введение
Важнейшим исходным моментом, необходимым для моделирования энергетических характеристик зданий, является доступность подробной информации о величинах данных диффузной и прямой освещенности. Кроме того, конфигурация и размер солнечных энергетических систем (например,грамм. фотоэлектрические элементы, солнечно-тепловые коллекторы) требует надежных измерений солнечной радиации.
Однако одновременные измерения общей и диффузной освещенности на горизонтальной поверхности или прямой нормальной освещенности доступны только для ограниченного числа местоположений. Измерение глобальной горизонтальной освещенности довольно просто и рентабельно. Возможно, он может быть неотъемлемой частью сенсорного оборудования каждого здания. Учитывая глобальные измерения солнечного излучения на горизонтальной поверхности (как наиболее широко доступные данные), прямые и рассеянные компоненты солнечного излучения могут быть получены с помощью различных корреляций.
Начиная с начала 1960-х годов, в литературе появились многочисленные модели для оценки диффузной составляющей, основанные на новаторской работе Лю и Джордана (1960), например, Orgill and Hollands, 1977, Erbs et al., 1982, Reindl et al. ., 1990, Lam and Li, 1996, Perez et al., 1990. Эти модели обычно выражаются в терминах полиномиальных функций от первой до четвертой степени, связывающих диффузную фракцию k d (отношение диффузного к глобальному солнечное излучение) с индексом четкости k t (отношение глобального солнечного излучения к внеземному на горизонтальной поверхности), а также с другими переменными, такими как высота Солнца, температура воздуха, относительная влажность.Хотя эти модели обычно создаются с использованием разумных подходов, их эффективность, по-видимому, снижается, когда они применяются к регионам, отличным от тех, которые предоставили исходные данные для разработки модели (Soler, 1990, LeBaron and Dirmhirn, 1983, Tuller, 1976). Таким образом, необходимы дальнейшие исследования, чтобы лучше учесть влияние местных климатических факторов на характеристики модели (Wong and Chow, 2001, Boland et al., 2001, Jacovides et al., 2006).
В этом исследовании изучается применимость различных стандартных моделей, коррелирующих почасовую диффузную фракцию для Вены, Австрия, на основе их предыдущих заявленных характеристик и наличия необходимых данных измерений для сравнения моделей.
2. Подход
Для целей настоящего исследования было рассмотрено восемь моделей для оценки диффузной доли излучения, как описано в Erbs et al., 1982, Orgill and Hollands, 1977, Reindl et al., 1990, Lam and Ли, 1996 г., Скартвейт и Олсет, 1987 г., Лоуч и др., 1991 г., Максвелл, 1987 г., Виньола и МакДэниелс, 1984 г. Сравнение было основано на данных измерения освещенности в Вене, Австрия. На выбор моделей повлияла их предыдущая заявленная производительность, а также наличие необходимых данных измерений для сравнения моделей.Модели обычно включают математические формулировки с несколькими коэффициентами, значения которых обычно действительны для конкретного местоположения. После первого сравнения восьми моделей для дальнейшего анализа были выбраны три более эффективные. Таким образом, исходные версии модели сравнивались с модифицированными версиями с коэффициентами, скорректированными для лучшего соответствия данным Вены. С этой целью были применены функции аппроксимации полиномиальных кривых с использованием стандартного набора инструментов аппроксимации кривых в MATLAB (2010).Ниже приводится краткое описание выбранных моделей.
2.1. Модели
2.1.1. Модель Эрбса (ER)
Erbs et al. (1982) использовали прямые данные нормальной и глобальной освещенности на горизонтальной поверхности с 5 станций в США. Диффузная фракция k d определяется как
Интервал: k t ⩽ 0,22; k d = 1 — 0,09 k t
(1)
Интервал: 0.22⩽kt⩽0.8kd = 0.9511-0.1604kt + 4.39kt2-16.64kt3 + 12.34kt4
(2)
Интервал: k t > 0,8; k d = 0,165
(3)
kt = ItIo · sin (α) kd = IdIt
(4)
, где
Io = Isc · 1 + 0.33cos360n365 · cosθ2 (5)
2.1.2. Модель Reindl (RE)
Reindl et al. (1990) оценили диффузную фракцию k d на основе данных измерений глобальной и диффузной горизонтальной освещенности в 5 местах в США и Европе.Алгоритм рассматривает три характерных интервала с использованием следующих параметров: индекс ясности ( k t ), высота солнца ( α ), температура наружного воздуха ( T a ) и относительная влажность φ . В зависимости от значения индекса прозрачности диффузные фракции ( I d / I t ) рассчитываются по формулам. (6), (7), (8).
Интервал: 0 ⩽ k t ⩽ 0.3 k d = 1,0 — 0,232 k t + 0,0239sin α — 0,000682 T a + + + 0,019
03 03 03 2 Интервал: 0,3 < k t ⩽ 0,78 k d = 1,329 — 1,716 k t + 0,267sin α — 0,00351060 — 0,00351060 T + + 0.106 ϕ (7)
Интервал: k t ⩾ 0,78 k d = 0,426 k t
10 — 0,259 αs 10 + 0,259 T a + + 0,0734 ϕ(8)
2.1.3. Модель Orgill and Holands (OH)
Orgill and Hollands (1977) оценила диффузную фракцию k d , используя индекс прозрачности k t в качестве единственной переменной.Модель была основана на данных измерения глобальной и диффузной освещенности из Торонто. Соотношение между диффузной фракцией на горизонтальной поверхности k d и индексом четкости k t дается согласно уравнениям. (9), (10), (11), (12).
Интервал: k t <0,35 k d = 1 — 0,249 k t
(9)
010 ⩽ 0,35 т ⩽ 0.75 k d = 1,577 — 1,84 k t(10)
Интервал: k t > 0,75; k d = 0,177
(11)
Прямая освещенность I b получается с помощью:
2.1.4. Модель Лам и Ли (LL)
Лам и Ли (1996) вывели диффузную фракцию k d на основе данных измерений прямой и диффузной освещенности для Гонконга в соответствии с уравнениями.(13), (14), (15).
Интервал: k t ⩽ 0,15; k d = 0,977
(13)
Интервал: 0,15 < k t ⩽ 0,7; k d = 1,237 — 1,361 k t
(14)
Интервал: k t > 0,7; к d = 0.273
(15)
2.1.5. Модель Скартвейта и Олсета (SO)
Скартвейт и Олсет (1987) вывели диффузную фракцию k d как функцию индекса ясности k t , солнечной высоты, температуры и относительной влажности. Модель была протестирована на данных 10 станций по всему миру. Прямая освещенность I b получается из общей освещенности G t с использованием следующих уравнений:
Intervalkt
(17)
Интервал c 1 ⩽ k t ⩽ 1,09 c 2
ψ = 1- (1-d1) [d2c31 / 2 -d2) c32]
(18)
, где
c 2 = 0,87 — 0,56 e -0,06 α
(19)
c3 = 0,51d + sin 0,5)
(20)
d 1 = 0,15 + 0,43 e -0,06 α
(22)
Интервал: kt> 1.09c2ψ = 1-1.09c21-ξkt
(25)
, где
ξ = 1- (1-d1) d2c312 + (1-d2) c32
(26)
c3 ′ = 0,151 + sinπc4d3-0,5
(27)
2.1.6. Louche et al. модель (LO)
Louche et al. (1991) использовали индекс четкости k t для оценки прямого излучения k b согласно формуле. (29). Корреляция включает глобальные и прямые данные об освещенности для Аяччо (Корсика, Франция, 44,9 ° северной широты) в период с октября 1983 года по июнь 1985 года.
кб = -10.676kt5 + 15.307kt4-5.205kt3 + 0.99kt2-0.059kt + 0.02
(29)
2.1.7. Модель Максвелла (МА)
Квазифизическая модель для преобразования часовой глобальной горизонтальной инсоляции в прямую нормальную инсоляцию была предложена Максвеллом в 1987 году. Модель представляет собой комбинацию четкой физической модели с экспериментальной подгонкой для других условий. Прямое излучение I b рассчитывается по формулам. (30), (31), (32), (33), (34), (35), (36), (37), (38), (39).
I b = Io { ψ — ( d 4 + d 5 e m
)}(30)
ψ = 0.866-0.122ma + 0.0121ma2-0.000653ma3 + 0.000653ma4 + 0.000014ma5
(31)
где
Масса воздуха при стандартном давлении m r аппроксимируется формулой Кастена (Iqbal, 1978) согласно Уравнение (33).
м r = [cos θ z + 0,15 (93,885 — θ z ) -1,253 ]
-1и d 4 , d 5 и d 6 являются функциями индекса четкости k t , как показано ниже:
d4 = 0.512-1.56kt + 2.286kt2-2.222kt3
(34)
d 5 = 0.37 + 0.962 k t
(35)
d6 = -0.28 + 0.923kt 2.048kt2
(36)
d4 = -5.743 + 21.77kt-27.49kt2 + 11.56k
(37)
d5 = 41.4-118.5kt + 66.05kt2 + 31.9kt3
(38)
d6 = -47.01 + 184.2kt-222kt2 + 73.81kt3
(39)
2.1.8. Модель Виньолы и МакДэниелса (VM)
Виньола и МакДэниелс (1984) была создана на основе измерений на семи участках в Орегоне и Айдахо, США.Рассчитывается диффузная освещенность k d (см. Уравнение (40)) как функция индекса четкости ( k t ) и количества дней ( N ).
k d = 0,162 — 1,451 k t + 0,045sin [2 π ( N -40) / 365]
(40)
2.2. Измерения
Для сравнения моделей диффузной фракции измеренная глобальная и диффузная горизонтальная освещенность была получена с использованием станции микроклиматического мониторинга кафедры строительной физики и экологии зданий Венского технологического университета, Австрия (местоположение: 48 ° 12 ′ с.ш. , 16 ° 22′E).Учитывая высоту установки станции (самая высокая точка кампуса), высота эффективного горизонта из-за препятствий (например, окружающих зданий) незначительна.
Для этого исследования использовались два набора данных измерений. Один набор, который был собран за 17-месячный период (с января 2009 г. по май 2010 г.), использовался для сравнения производительности моделей. Второй набор измерений, который использовался для получения локальной (венской) версии трех более эффективных моделей, содержал измеренные данные глобальной освещенности, собранные за двухлетний период (с января 2007 г. по декабрь 2008 г.).
Чтобы получить значения адаптированных коэффициентов, были применены функции аппроксимации полиномиальной кривой с использованием стандартного набора инструментов аппроксимации кривой в программном обеспечении MATLAB (2010).
Измерения глобальной горизонтальной и диффузной освещенности проводились каждые 5 минут в светлое время суток, охватывая различные условия неба, от солнечного до частично облачного и пасмурного.
После всесторонней проверки качества данных в исследование были включены 32 265 пар измеренных значений энергетической освещенности в первой базе данных и 47 087 пар во второй базе данных.
Глобальные измерения горизонтальной освещенности ниже 50 Вт · м −2 и измерения на высоте солнца менее 5 ° были удалены из наборов данных, учитывая сравнительно менее точные характеристики датчика в этих диапазонах. Обратите внимание, что компоненты датчиков станции мониторинга Департамента строительной физики и экологии зданий регулярно калибруются через сертифицированные агентства.
Технические характеристики применяемого пиранометра и метеорологической метеостанции приведены в.
Таблица 1
Входные параметры для восьми моделей диффузной фракции.
Модели Orgill and Holland Erbs Reindl Lam and Li Skartveit and Olseth Louche Maxwell Vignola и ERDaniels 79 OH
79 Коды моделей
RE LL SO LO MA VM Глобальная освещенность I t x x x x x x Солнечная постоянная I o x x x x x x x x 21 α Солнечная высота x x x x x x x x Относительная влажность Φ x Температура воздуха T a Местное давление воздуха p x Чтобы получить необходимый входной параметр для восьми моделей диффузной фракции (см.) одновременно с радиометрическими измерениями метеостанция в том же месте отслеживала другие внешние параметры окружающей среды, такие как температура воздуха и относительная влажность.
Таблица 2
Обзор технических характеристик КИПиА.
Датчик Информация Глобальная и диффузная освещенность (солнечный пиранометр SPN1) Общая точность: ± 5% суточных интегралов, ± 5% ± 10 Вт · м 2 среднечасовые ± 8% ± 10 Вт · м 2 отдельные показания Разрешение: 0,6 Вт · м 2 = 0,6 мВ, диапазон: от 0 до> 2000 Вт · м 2 , порог состояния солнечного света: 120 Вт · м 2 дюйма прямой луч, диапазон температур: от -20 до +70 ° C, точность: косинусная коррекция ± 2% входящего излучения при зенитном угле 0–90 дюймов, точность: азимутальный угол ± 5% при вращении на 360 °, время отклика <200 мс Метеостанция мониторинга Наружная температура: Абсолютная ошибка: <0.3 К; Диапазон температур: от −30 до +70 ° C; Время отклика <20 с (≥1,5 мс −1 ) Относительная влажность вне помещения: Абсолютная погрешность: <± 2%; Диапазон влажности: 0–100%; Время отклика <10 с (≥1,5 мс −1 ) Скорость ветра: Абсолютная ошибка: <1%; Диапазон скорости ветра 0–75 м с −1 2.3. Сравнение моделей
Для сравнения производительности моделей использовались три общих статистических показателя, а именно относительное среднее отклонение смещения MBD (уравнение.(41)), относительной погрешности (уравнение (42)) и среднеквадратичного отклонения RMSD (уравнение (43)).
MBD = ∑i = 1nIdm (i) -Idc (i) Idm (i) n × 100 (%)
(41)
REi = Idm (i) -Idc (i) Idm (i) × 100 (%)
(42)
RMSD = ∑i = 1n [(Idm (i) -Idc (i)) / Idm (i)] 2n (Wm-2)
(43)
В этих уравнениях , I dm ( i ) означает измеренную диффузную освещенность, I dc ( i ) общее количество пар измеренных и вычисленных значений.
3. Результаты
Для сравнения производительности восьми моделей диффузных фракций (версий с исходными коэффициентами) показана кумулятивная функция распределения (CDF) относительных ошибок (в ±%) для восьми моделей с исходными коэффициентами. перечисляет эту информацию в числовом виде для дискретных значений относительной погрешности (от ± 5% до ± 40%). сравнивает восемь вариантов с точки зрения RMSD и MBD.
Кумулятивная функция распределения (CDF) относительных ошибок (в ±%) для восьми моделей с исходными коэффициентами.
Таблица 3
Процент результатов с соответствующей максимальной относительной ошибкой (в ±%) для исходных версий восьми моделей по сравнению с данными Вены.


 ш. 50° 10′ в.д.
ш. 50° 10′ в.д.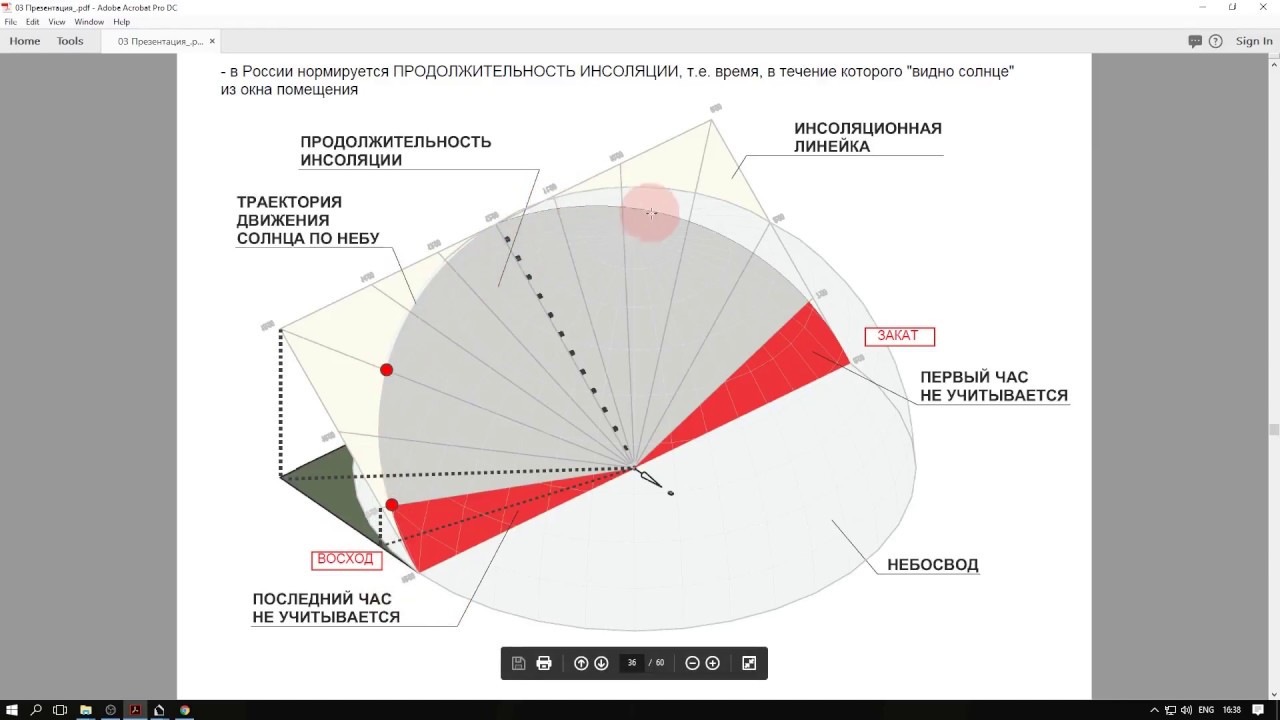 93° 4′ в.д.
93° 4′ в.д. ш. 104° 14′ в.д.
ш. 104° 14′ в.д. ш. 37° 36′ в.д.
ш. 37° 36′ в.д.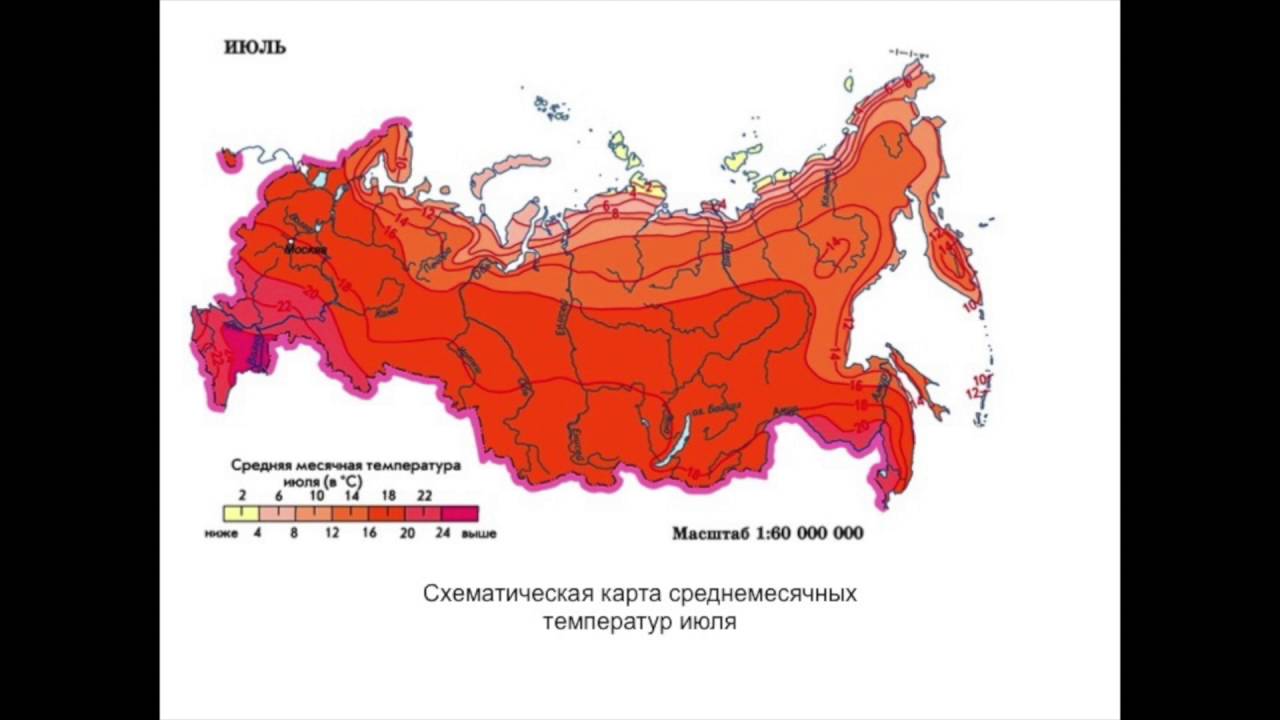 д.
д.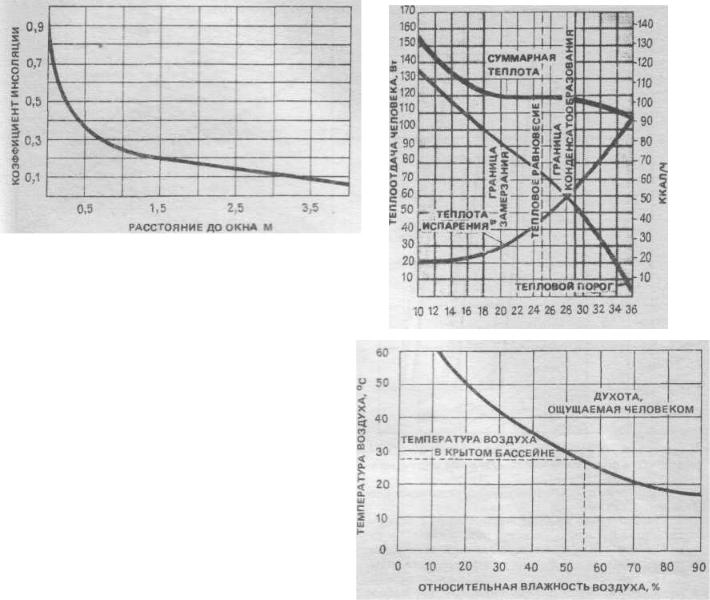 ш. 32° 3′ в.д.
ш. 32° 3′ в.д. ш. 45° 10′ в.д.
ш. 45° 10′ в.д. ш. 101° 43′ в.д.
ш. 101° 43′ в.д. ш. 76° 32′ в.д.
ш. 76° 32′ в.д. ш. 37° 17′ в.д.
ш. 37° 17′ в.д. ш. 61° 56′ в.д.
ш. 61° 56′ в.д. ш. 41° 8′ в.д.
ш. 41° 8′ в.д. ш. 38° 47′ в.д.
ш. 38° 47′ в.д. ш. 43° 4′ в.д.
ш. 43° 4′ в.д.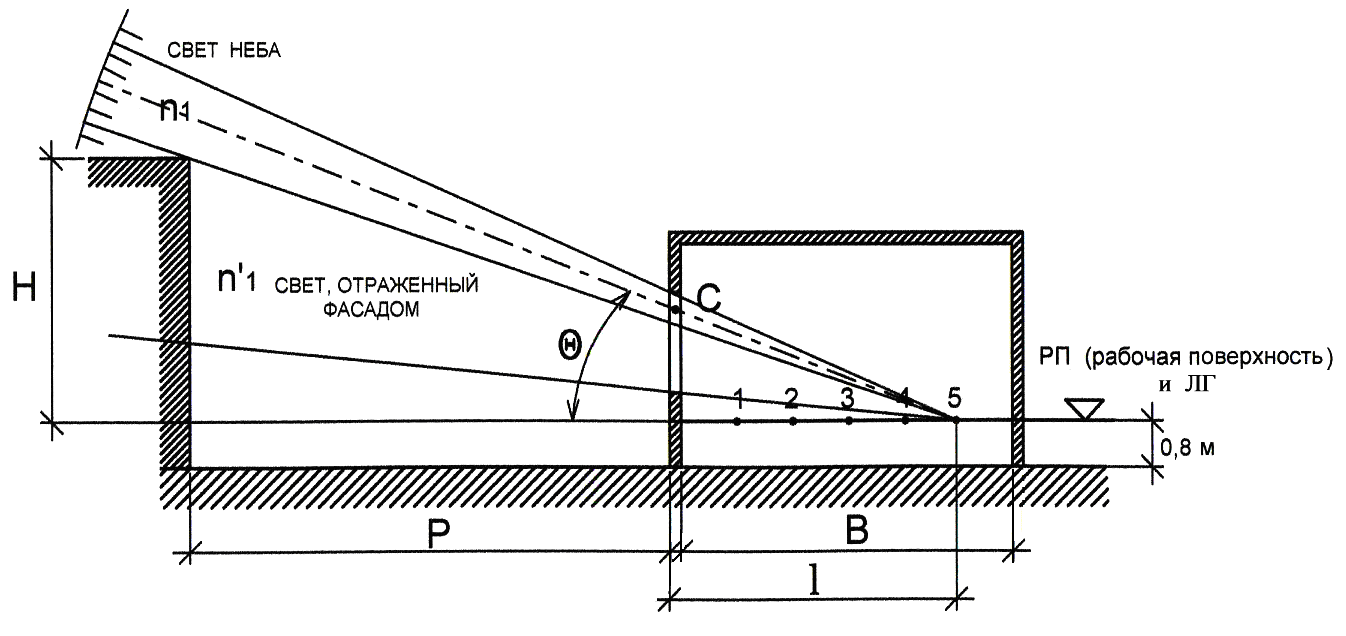 ш. 45° 24′ в.д.
ш. 45° 24′ в.д. ш. 38° 29′ в.д.
ш. 38° 29′ в.д.