В 1 кубе сколько пеноблоков: расчеты и инструкция
Любой стеновой материал измеряется в трех единицах: штуках, кубических и квадратных метрах.
При покупке пенобетонных блоков стоимость зачастую указывается за 1 куб. м, что не совсем понятно для обычного человека, который столкнулся с этим впервые.
В результате возникает вопрос: как определить, сколько в 1 кубе пеноблоков?
Расчет достаточно простой, ведь для того чтобы узнать объем одного камня достаточно измерить его стороны: длину, высоту, ширину. Исходя из этих данных, можно будет получить необходимые результаты. Узнать что лучше: пеноблок или газоблок можно тут.
Как вычислить, сколько пеноблоков в 1 кубе?
Объем блока полностью зависит от собственных параметров, так как стеновой материал изготавливается в разных типоразмерах. Будет более понятным, если рассматривать на примерах:
- Пенобетон 600 х 300 х 200 мм весит 22 кг. Для того чтобы выполнить расчет необходимо миллиметры перевести в метры и все стороны перемножить: 0,6 х 0,3 х 0,2=0,036 куб.
- Стеновой материал 600 х 300 х 100 мм весит в два раза меньше 11 кг, это значит, его объем на половину меньше, а количество в 2 раза больше: 0,6 х 0,3 х 0,1=0,018 куб. м. или 1/0,018=55,56≈56 единиц.
- Камень размерами 600 х 300 х 240 мм весит 28 кг, имеет объем 0,0432 куб. м (0,6 х 0,3 х 0,24) и количество в 1 куб. м составляет 23 единицы (1/0,432).
- Пенобетон 600 х 400 х 200 мм имеет объем 0,048 куб. м и 21 единицу в 1 куб. м.
Зная, сколько в 1 кубе пеноблоков штук, проще будет определиться, какие размеры лучше всего подойдут для строительства дома, дачи, гаража. Количество материала зависит от высоты и толщины несущей стены. Какая плотность пенобетона и характеристики пенобетонных блоков смотрите в соответствующих статьях.
Что еще необходимо учитывать при расчете стенового материала?
Сделав предварительные подсчеты и узнав в 1 кубе, сколько пеноблоков, можно смело покупать стеновой материал в том количестве, которое получилось в конечном результате.
Но, если учитывая то, что за один искусственный камень нужно будет заплатить немалую сумму, приходится задумываться о жесткой экономии.
Кладка камня осуществляется при помощи раствора, от выбора которого зависит толщина слоя:
- раствор цементно-песчаный – 1-2 см;
- клеевой состав – 2-3 мм.
Поэтому резонно произвести более тщательные расчеты, чтобы узнать, сколько в 1 кубе пеноблоков с раствором цементно-песчаным, так как применяя клеевой состав малая толщина слоя не сможет особо повлиять на количество стенового материала. Рекомендуем просмотреть статью и узнать что такое монолитный пенобетон.
Важно! Также при строительстве дома необходимо знать, сколько метров площади в 1 кубе пеноблоков.
Для того чтобы рассчитать площадь камня нужно высоту умножить на длину и получится цифра кв. м:
- Пенобетон размером 600 х 300 х 200 мм имеет площадь 0,18 кв.м.
- Если одна стена дома составляет 27 кв. м (3 х 9), тогда можно рассчитать количество камня, применив формулу: 27/0,18=150 единиц, соответственно в кубических метрах цифра будет 150х0,036=5,4 куб. м.
м.Зная все варианты расчетов стенового материала, можно выбирать наиболее удобный способ или использовать несколько, чтобы удостовериться в правильности полученного результата. Важными показателями являются толщина стены и слоя раствора. Как перевезти ЖБИ читайте здесь.
Советы как быстро перевести брус в кубометры
На самом деле перевод доски или бруса из штук в кубы и наоборот совсем не сложный. Для этого нужно определить объем одной доски, учитывая ее ширину, толщину и длину.
Определение объема одной доски
Возьмем в качестве примера самую популярную доску 50х150, т.е. доску толщиной 5 см, шириной 15 см. Стандартная длина нестроганой доски — 6 м (6000 мм). Чтобы получить объем в кубических метрах, нужно умножить все размеры доски, выраженные в метрах, в данном случае:
0,05 х 0,15 х 6,0 = 0,045
Таким образом, объем одной доски равен 0,045 куб.
Определение объема одного бруса
Брус это такая же доска, только толстая. Самый популярный брус 150х150, т.е толщина и высота по 15см, стандартная длина — 6 метров. Переводим все размеры в метры, умножаем и получаем 0,135 куб.метра:
0,15 х 0,15 х 6,0 = 0,135
Сколько досок в одном кубе
Казалось бы тут все просто. Делим 1 куб на объем одной доски и получаем количество досок. Например, для нашей доски 50х150: 1 / 0,045 = 22,22…
А для бруса 150х150: 1 / 0,135 = 7,40740…
Все было бы хорошо, но в одном кубе не целое количество досок и брусьев.
Не все так просто
Вот тут-то нас и ловят ушлые розничные продавцы леса. Один куб доски — пожалуйста — 22 штуки, один куб бруса — получите 7 брусов. Например, для маленького домика 6х6 нужно 52 бруса — если вам считают 52/7= 7,43 кубов, то вас обманывают уже на 3 бруса.
Как правильно считать
Самое правильное — заранее посчитать не количество кубов, а количество единиц пиломатериала.
Рассмотрим тот же пример — 52 бруса длиной 6 метров сечением 150х150.
Считаем общий объем:
0,15 х 0,15 х 6,0 х 52 = 7, 02 куб.метра.
Вот за эти 7,02 куба вы и должны заплатить, получив ровно 52 бруса, причем и объем в куб.метрах, и количество бруса должны быть указаны в накладной.
Другие хитрости пиломатериала
На практике существует понятие «калиброванные» и «некалиброванные» пиломатериалы. Они имеют разные допустимые отклонения от заданных размеров, но и стоят по-разному. Вы должны заранее определить, какие допуски важны, а какие нет. Если вы используете брус 100х150 для соединения СИП-панелей, то калиброванный пиломатериал просто необходим, тут даже электрорубанок не поможет, т.к. некалиброванный материал обычно имеет меньшие размеры.
Еще одна особенность — длина, превышающая 6 метров. Обычно средний размер доски или бруса не 6 метров, а 6,05. Это связано с тем, что торцы не обработаны в процессе распила, могут быть грязными или идти под разными углами.
Сколько мешков смесей пескобетона в одном кубометре
Перед покупкой сухих цементно-песчаных смесей для стяжки пола необходимо определить, сколько упаковок следует приобрести для заливки пола данной площади. При расчете затрат следует учитывать несколько факторов. Расход материала зависит от цели использования, типа поверхности, толщины стяжки, плотности и марки раствора. Рассмотрим подробнее, сколько весит куб сухой смеси, как рассчитать требуемое количество мешков и перевести значение в кубометры.
Особенности расчета пескобетона
Бетон на основе пескобетона используется на различных стадиях строительства и ремонта. Расход зависит от марки сырья и его плотности. Раствор включает такие компоненты:
- песок с размером фракций до 3 мм;
- портландцемент 1 сорта;
- добавки, улучшающие прочность;
- пластификаторы, повышающие устойчивость к влаге;
- гранитный порошок или мой упаковке весом 25, 30, 40 или 50 кг в зависимости от производителя.
При расчете затрат на каждый квадратный метр учитывается состояние основания, толщина стяжки и пропорции замеса. В среднем при заливании слоя 1 см на 1 м2 понадобится 20 кг марки М300. Полы с дефектами невозможно исправить более тонким слоем.
Определение затрат раствора на площадь пола в квартире выполняют по формуле. Рассмотрим расчет необходимого количества пескобетона на примере квартиры площадью 90 м2. Стяжку выполняют слоем 1-10 см. Пусть в нашем примере слой заливки будет составлять 5 см.
На каждый квадратный метр стяжки толщиной 1 см понадобится 20 кг сухой смеси, его умножаем на высоту стяжки 5 см и получаем 100 кг пескобетона. Полученный результат умножаем на площадь 90 м2. Для ремонта поверхности всего пола необходимо предусмотреть 9 тысяч кг материала. В пересчете на мешки получим: 180 пакетов по 50 кг или 360 пакетов по 25 кг.
Важно! Чтобы вычислить требуемое число упаковок, общий вес сухой смеси, требующейся для всей площади пола, делим на количество килограмм в одном пакете.
В нашем примере 9000 кг делим на 50 кг или 25 кг соответственно.Как вычислить затраты на один куб раствора?
Материал относят к тяжелым бетонам, плотность 1 м3 его составляет 500-2500 кг/м3 в зависимости от марки смеси. Для вычислений затрат на один куб чаще всего используют параметр 2400 кг/м3 для марки М300. Данную марку чаще всего используют для строительных работ. Другими словами каждый куб весит 2,4 тонны.
Чтобы высчитать количество пескобетона на 1 м3, массу делят на вес одного мешка. В нашем случае при заливке 2400 кг понадобится 48 упаковок по 50 кг. Для других марок удельный вес одного куба смеси следует посмотреть в технической документации. Производители строительных материалов на упаковке указывают только расход на квадратный метр площади. Пересчет в кубометрах применяют при определении затрат в процессе обустройства фундамента и возведения монолитных конструкций.
Количество пескобетона для выравнивания основания
При классическом расчете расхода сухой смеси на квадратный метр не учитываются особенности основания.
Заливка в большинстве случаев применяется для выравнивания старого пола и исправления погрешностей перед укладкой финишных покрытий. Для исправления выпуклостей, впадин, перепадов по высоте необходимо правильно рассчитать толщину стяжки.
Сколько кубов пескобетона входит в один мешок, определяют по формуле. Вес упаковки следует разделить на массу одного куба смеси. Например, 50 кг делим на 2400 кг. В данном случае в упаковку весом 50 кг входит 0,02 м3 сухого порошка. Сокращает расход материала добавка в бетон заполнителей в виде щебня и гранитной крошки.
Таблица расхода пескобетона
Площадь помещения в м2 следует разделить на соответствующий коэффициент в таблице:
| Толщина слоя | 1 см | 1,5 см | 2 см | 2,5 см | 3 см | 3,5 см | 4 см | 4,5 см | 5 см | 6 см | 7 см | 8 см | 9 см | 10 см |
| Вес мешка | ||||||||||||||
| 40 кг | 2,6 | 2,4 | 1,8 | 1,3 | 0,9 | 0,75 | 0,6 | 0,52 | 0,45 | 0,4 | 0,36 | 0,3 | 0,25 | 0,22 |
| 50 кг | 3,1 | 2,75 | 2,25 | 1,67 | 1,12 | 0,93 | 0,75 | 0,65 | 0,56 | 0,5 | 0,45 | 0,37 | 0,32 | 0,28 |
Для штукатурных работ учитывают только площадь стены и параметры слоя.
На кирпичных поверхностях и полах со швами предусматривают затраты на проникновение жидкости в щели, полости и пустоты. Для выравнивания пола раствор заливают толщиной 7-10 см в зависимости от размера перепадов, более тонкая стяжка для этой цели непригодна.
Чтобы рассчитать правильно толщину слоя, составляют «карту перепадов». По всему помещению на каждый квадратный метр площади на стенах наносят метки в соответствии с требуемыми параметрами заливки. Горизонтальность предварительно выставляют с помощью лазерного уровня. Все значения суммируют и делят на количество меток. Итоговый параметр используется в качестве средней величины.
Почему следует заказать пескобетон в компании «АльфаЦем»
Мы предлагаем большой ассортимент сухих смесей от крупнейших производителей по оптовым ценам. Доставка товаров осуществляется круглосуточно в соответствии с потребностями вашего производства. К достоинству наших услуг относят:
- бесплатные консультации по вопросам выбора продукции и оформления заказа;
- отсутствие регистрации на сайте, возможность отследить товар в пути следования к вам;
- возможность самовывоза со складов в Московской области;
- наличие сертификатов, подтверждающих качество всех материалов.
По Москве осуществляем транспортировку силами нашего автотранспорта грузоподъемностью 5-25 тонн. Позвоните в «АльфаЦем» сейчас и мы просчитаем стоимость кубометра с учетом доставки и выгрузки на объекте с привлечением манипулятора.
Перевести единицы площади и объема
Цель урока — преобразовать единицы измерения между измерениями, включая область а также объем .
Область:
Площадь измеряется в квадратных единицах (ед. 2 ).
Пример 1:
Преобразуйте один квадратный ярд в квадратные футы.
Квадратный ярд — это квадрат со стороной в один ярд.
Мы знаем это, 1 двор = 3 ноги.
Так, 1 квадратный ярд — это квадрат со стороной 3 ноги.
Вы можете использовать формулу площади квадрата,
А
знак равно
s
2
, чтобы преобразовать квадратные единицы.
С 1 двор = 3 ноги, заменить s от 3 .
А знак равно ( 3 ) 2 знак равно 9
Так, 1 квадратный ярд равен 9 квадратный фут.
Обычные преобразования для квадратных единиц
В таблице приведены несколько распространенных преобразований единиц измерения квадратных.
| Обычные единицы | Метрические единицы |
| 1 ярд 2 знак равно 9 футов 2 | 1 м 2 знак равно 10 , 000 см 2 |
| 1 футов 2 знак равно 144 в 2 | 1 см 2 знак равно 100 мм 2 |
Объем
Объем измеряется в кубических единицах (ед.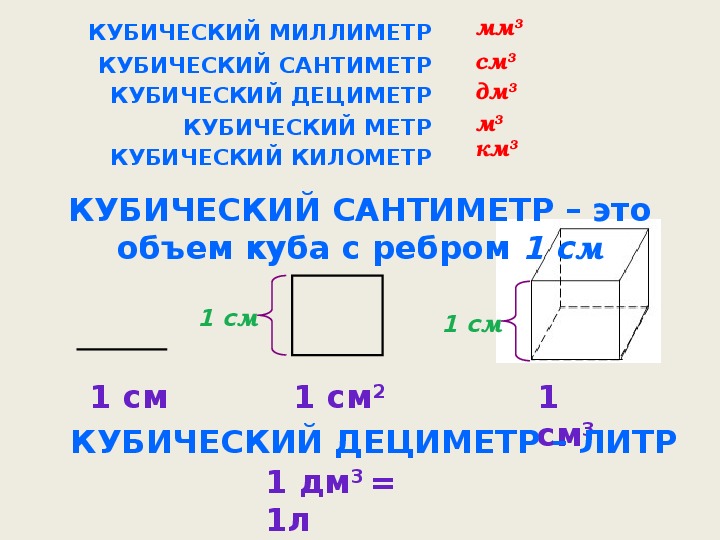
3 ).
Пример 2:
Перевести один кубический фут в кубические дюймы.
Кубический фут — это куб со стороной в один фут.
Мы знаем это, 1 фут = 12 дюймы.
Так, 1 кубический фут — это куб с длиной стороны 12 дюймы.
Вы можете использовать формулу объема призмы, V знак равно б ш час , чтобы преобразовать кубические единицы.
С 1 фут = 12 дюймы, заменить б , ш , а также час с участием 12 .
V знак равно ( 12 ) ( 12 ) ( 12 ) знак равно 1 , 728
Так,
1
кубический фут равен
1,728
кубические дюймы.
Обычные преобразования для кубических единиц
В таблице приведены несколько распространенных преобразований единиц измерения в кубические единицы.
| Обычные единицы | Метрические единицы |
| 1 ярд 3 знак равно 27 футов 3 | 1 м 3 знак равно 1 , 000 , 000 см 3 |
| 1 футов 3 знак равно 1 , 728 в 3 | 1 см 3 знак равно 1 , 000 мм 3 |
В
метрическая система
также связаны длина, масса и вместимость.
1 миллилитр имеет тот же объем, что и 1 кубический сантиметр. ( 1 мл = 1 cc)
1 миллилитр воды примерно 1 грамм. ( 1 мл ≈ 1 грамм )
Примечание:
А длина измеряется в единицы измерения , область измеряется в квадратные единицы ( Ед. изм × Ед. изм знак равно Ед. изм 2 ) , а также объем измеряется в кубические единицы ( Ед. изм × Ед. изм × Ед. изм знак равно Ед. изм 3 ) .
открытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
Класс 7A
Марка 7Б
7 класс (A и B вместе)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 8A
Сорт 8Б
8 класс (A и B вместе)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
9 класс (A и B вместе)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 4A
Класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5A
Марка 5Б
Оценка 5 (вместе A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 6А
Марка 6Б
6 класс (A и B вместе)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.
Вы можете делать ксерокопии, распечатывать и распространять их сколь угодно часто. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без марочного знака)
Эти небрендовые версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Определение объема и площади поверхности куба
Результаты обучения
- Найдите объем и площадь поверхности куба
Куб — это твердое тело прямоугольной формы, длина, ширина и высота которого равны.{2} [/ латекс].
Объем и площадь куба
Для любого куба со сторонами длиной [латекс] с [/ латекс],
пример
Куб [латекс] 2,5 [/ латекс] дюйма с каждой стороны. Найдите его 1. объем и 2. площадь поверхности.
Решение
Шаг 1 одинаков для 1. и 2., поэтому мы покажем его только один раз.
| Шаг 1. Прочтите о проблеме. Нарисуйте фигуру и пометьте его данной информацией.{3} [/ латекс] [латекс] V = 15,625 [/ латекс] | |
Шаг 6. Проверка: Проверьте свою работу. | |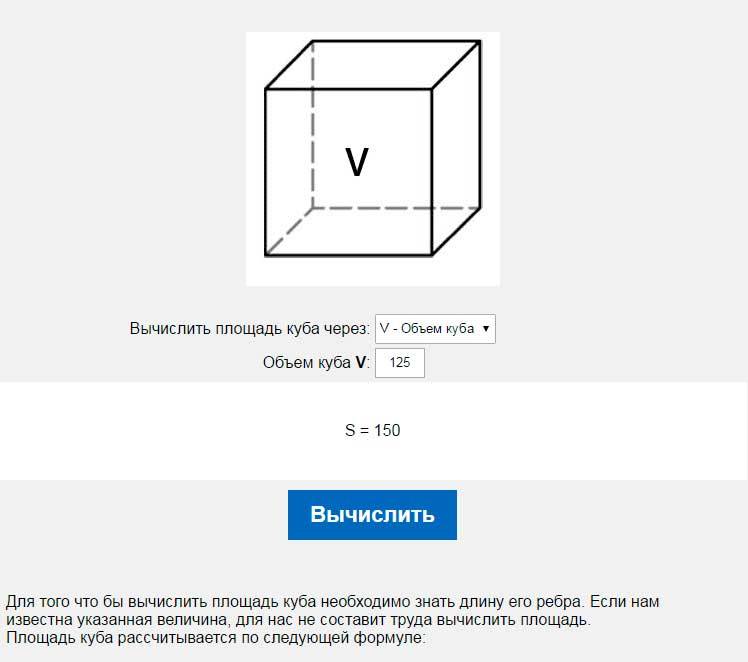
| Шаг 7. Ответьте на вопрос. | Объем [латекс] 15,625 [/ латекс] кубических дюймов. |
| 2. | |
| Шаг 2. Определите , что вы ищете. | Площадь поверхности куба |
| Шаг 3. Имя.{2} [/ латекс] [латекс] S = 37,5 [/ латекс] | |
| Шаг 6. Чек: Чек остается на ваше усмотрение. | |
| Шаг 7. Ответьте на вопрос. | Площадь поверхности [латекс] 37,5 [/ латекс] квадратных дюймов. |
пример
Кубик для блокнота размером [латекс] 2 [/ латекс] дюйма с каждой стороны. Найдите его 1. объем и 2. площадь поверхности.
Показать решениеРешение
Шаг 1. Прочтите проблему. Нарисуйте фигуру ипометьте его данной информацией. |
| 1. | |
| Шаг 2. Определите , что вы ищете. | объем куба |
| Шаг 3. Имя. Выберите переменную для ее представления. | let V = объем |
| Шаг 4. Перевести. Напишите соответствующую формулу.{3} [/ латекс] [латекс] V = 8 [/ латекс] | |
| Шаг 6. Проверка: Убедитесь, что вы выполнили расчеты правильно. | |
| Шаг 7. Ответьте на вопрос. | Объем [латекс] 8 [/ латекс] кубических дюймов. |
| 2. | |
| Шаг 2. Определите , что вы ищете. | Площадь поверхности куба |
Шаг 3.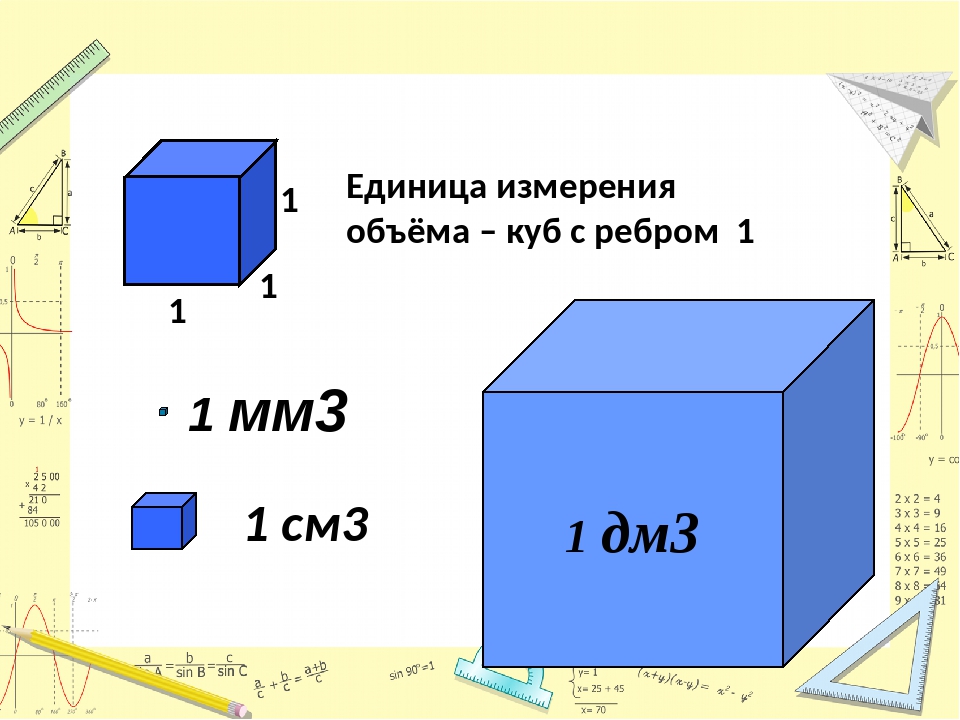 {2} [/ латекс][латекс] S = 24 [/ латекс] | |
| Шаг 6. Чек: Чек остается на ваше усмотрение. | |
| Шаг 7. Ответьте на вопрос. | Площадь поверхности [латекс] 24 [/ латекс] квадратных дюймов. |
Площадь поверхности куба
Компании упаковывают предметы в коробки по площади поверхности, чтобы определить, сколько картона потребуется для изготовления коробки.Это важно для определения суммы, необходимой для изготовления коробок, и для определения стоимости.Чтобы вычислить площадь поверхности, нам нужно включить площадь каждой стороны коробки. Каждая сторона куба представляет собой квадрат, такой же, как и все остальные квадраты, использованные для создания куба.
Это упрощает расчет площади поверхности. Определите площадь одного из квадратов по формуле A = s 2 . Затем умножьте на 6, потому что есть 6 равных сторон.
Давайте попробуем!
Площадь синего куба составляет 150 квадратных сантиметров.
Пример:
Определите площадь поверхности куба.
Решение:
Если вам сложно работать с дробью, переводите в десятичную!
Площадь поверхности этого куба составляет 37,5 квадратных дюймов.
Если вам известна площадь поверхности, вы также можете работать в обратном направлении, чтобы определить длину сторон.
Пример: Площадь поверхности куба составляет 86,64 квадратных метра. Определите длину стороны куба.
Решение: Поскольку нам уже известна площадь поверхности, мы можем работать в обратном порядке по шагам, чтобы определить длину стороны.
Длина стороны была возведена в квадрат, а затем умножена на 6. Итак, мы разделим на 6, чтобы отменить умножение. Затем мы извлечем квадратный корень, чтобы отменить возведение в квадрат.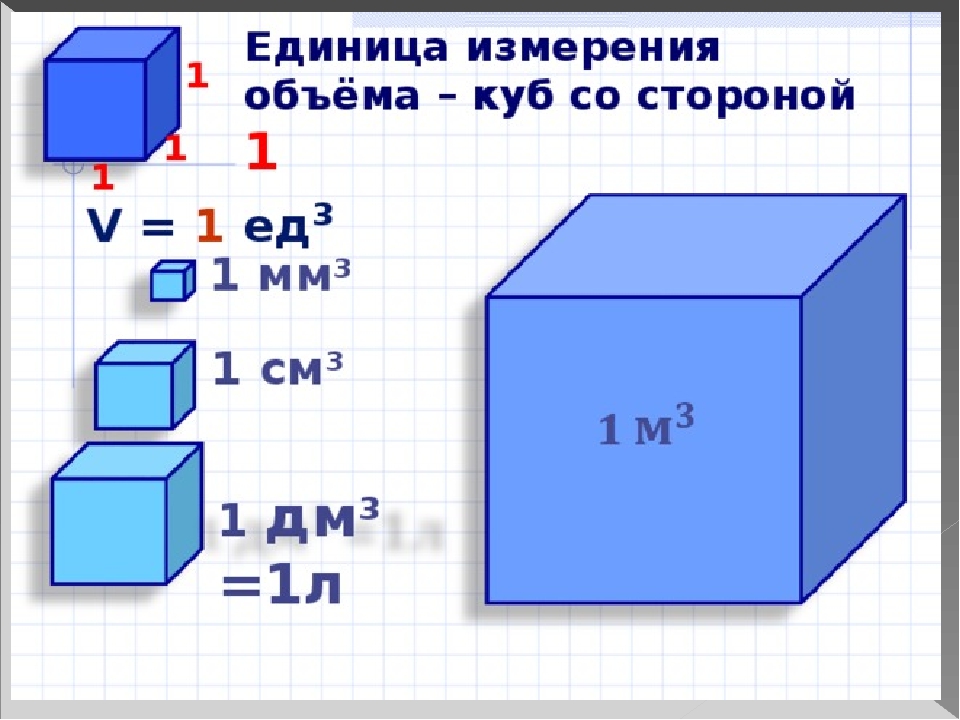
Следовательно, сторон куба по три.8 метров в длину.
Пример: Площадь поверхности куба составляет 384 м 2 . Определите объем куба. Решение: нам нужно знать длину стороны, чтобы определить объем. Итак, первый шаг — работать в обратном направлении от поверхности стороны длины.
Длина стороны куба 8 метров.
Теперь используйте это значение для определения объема по формуле V = s 3 .
Объем куба — 512 кубометров.
Давайте рассмотрим
Чтобы определить площадь поверхности куба, вычислите площадь одной из сторон квадрата, а затем умножьте его на 6, потому что у него 6 сторон. Это то же самое, что и решение по формуле SA = 6s 2 . Если вам дана площадь поверхности, вы можете определить длину стороны, работая в обратном направлении. Возьмите площадь поверхности и работайте в обратном направлении, разделив на 6, а затем извлеките квадратный корень.
Площадь поверхности куба
Чтобы вывести формулу площади поверхности куба, вам нужно будет начать с куба, как показано ниже, и назвать длину одной стороны a.
Для того, чтобы сделать куб, подобный показанному выше, вам в основном необходимо использовать следующий шаблон куба:
Глядя на шаблон куба, легко увидеть, что куб имеет шесть сторон, и каждая сторона представляет собой квадрат.
Поскольку длина ребра равна a, площадь одного квадрата равна a × a = a 2
Поскольку имеется шесть сторон, общая площадь поверхности, назовем ее SA, может быть найдена, как показано ниже:
SA = a 2 + a 2 + a 2 + a 2 + a 2 + a 2
SA = 6 × a 2
Несколько примеров, показывающих, как найти площадь поверхности куба
Пример № 1:
Найдите площадь поверхности, если длина одной стороны составляет 3 см.
Площадь поверхности = 6 × a 2
Площадь поверхности = 6 × 3 2
Площадь поверхности = 6 × 3 × 3
Площадь поверхности = 6 × 9
Площадь поверхности = 54 см 2
Пример № 2:
Найдите площадь поверхности, если длина одной стороны составляет 5 см.
Площадь поверхности = 6 × a 2
Площадь поверхности = 6 × 5 2
Площадь поверхности = 6 × 5 × 5
Площадь поверхности = 6 × 25
Площадь поверхности = 150 см 2
Пример № 3:Найдите площадь поверхности, если длина одной стороны составляет 1/2 см.
Площадь поверхности = 6 × a 2
Площадь поверхности = 6 × (1/2) 2
Площадь поверхности = 6 × 1/2 × 1/2
Площадь поверхности = 6 × 1/4
Площадь поверхности = 6/4 см 2
Площадь поверхности = 3/2 см 2
Площадь поверхности = 1,5 см 2
Пример 4:
Найдите площадь поверхности, если длина одной стороны 2 1/3 см.
Сначала преобразуйте 2 1/3 в правильную дробь.
2 1/3 = (2 × 3 + 1) / 3 = (6 + 1) / 3 = 7/3
Площадь поверхности = 6 × a 2
Площадь поверхности = 6 × (7/2 ) 2
Площадь поверхности = 6 × 7/2 × 7/2
Площадь поверхности = 6 × 49/4
Площадь поверхности = 294/4 см 2
Площадь поверхности = 73,5 см 2
Метрическая система: кубические единицы
Метрическая система: кубические единицыМетрические кубические единицы: преобразование одной кубической единицы в другую
Десять примеров
Проб 1-10
Вернуться в меню метрической системы
Процесс решения во многом такой же, как и при решении задач с квадратными единицами, за исключением того, что вам нужно возвести в куб абсолютное экспоненциальное расстояние между двумя префиксами.
Я буду использовать те же примеры, что и в учебнике по квадратным единицам, за исключением кубических задач.
Помните, что кубические задачи имеют дело с объемом.
Пример № 1: Преобразование 1,00 м 3 в кубические сантиметры.
Решение:
1) Вот настройки для преобразования:
??? см 3 1,00 м 3 x ––––––– = ответ 1 м 3 Обратите внимание, что m 3 отменяет, оставляя cm 3 в качестве единицы в ответе.
2) Некоторое обсуждение:
Абсолютное экспоненциальное расстояние между базовой единицей и сантиметрами составляет 10 2 . Иногда учитель может сказать, что экспоненциальное расстояние равно 2. Имейте в виду, что 2 — это показатель степени, а НЕ то, что вы будете умножать что-то на 2. В кубической ситуации мы должны превратить это в куб, чтобы получить 10 6 . Причина, по которой мы это делаем, заключается в том, что есть три измерения сантиметра, по одному для каждой из трех сторон куба.
3) Позвольте мне предвидеть проблему:
Вы читаете вышесказанное и говорите: «Подождите, куб 2 равен 8, не так ли?» Вы правы, потому что (2) 3 = 2 x 2 x 2 = 8, но мы имеем дело с экспоненциальным значением 2, а не с числом 2.В кубе получается 10 2 , а не 2. Мы бы написали (10 2 ) 3 = 10 2 x 3 = 10 6 .
4) Теперь, чтобы закончить пример:
10 6 см 3 1,00 м 3 x ––––––– = 1,00 x 10 6 см 3 1 м 3 Вы также можете увидеть это так:
(1.00 м 3 ) (10 6 см 3 / м 3 ) = 1,00 x 10 6 см 3
Пример № 2: Преобразование 1,00 км 3 в кубические микрометры.
Решение:
1) Проблема заключается в преобразовании:
??? мкм 3 1.00 км 3 x ––––––– = ответ 1 км 3 Обратите внимание, что km 3 отменяется, оставляя μm 3 в качестве единицы в ответе.
2) Некоторое обсуждение:
Между кило- и микро- это абсолютное расстояние 10 9 . Наша методика требует куба экспоненциальной величины, поэтому (10 9 ) 3 = 10 27 . Направление изменения идет от большего префикса к меньшему, поэтому знак экспоненты в ответе будет положительным.
3) Завершите пример:
10 27 мкм 3 1.00 км 3 x ––––––– = 1,00 x 10 27 мкм 3 1 км 3
В двух приведенных выше примерах переход от большего префикса к меньшему. Это означало, что в одном большом префиксе было много меньшего префикса. Примеры ниже пойдут в противоположном направлении. Спросите себя: сколько префиксов большего размера содержится в одном маленьком префиксе? Ответ = меньше единицы, поэтому знак экспоненты будет отрицательным.
Сказав это, остерегайтесь проблемы, в которой показатель степени уже присутствует в задаче, а изменение отрицательной экспоненты не может подавить показатель степени из задачи. В этом случае в ответе будет положительный показатель степени.
Пример № 3: Преобразование 4310 кубических сантиметров в м 3 .
Решение:
1 3 м 3 4310 см 3 x ––––––– = 4.31 x 10 ¯ 3 м 3 (10 2 ) 3 см 3 Обратите внимание, как 1 в факте преобразования связана с большей (m 3 ) из двух единиц. Больше здесь означает, что 1 м 3 больше 1 см 3 .
Пример № 4: Преобразование 86,3 кубических сантиметра в 3 мм.
Решение:
86,3 см 3 x (10 3 мм 3 /1 3 см 3 ) = 8,63 x 10 4 мм 3В одном см 10 мм, поэтому 10 x 10 x 10 дает 10 3 мм 3 .
Пример 5: 5,94 x 10 10 мм 3 . Перевести в дм 3 . Затем переведите в литры.
Решение:
1 дм 3 5.94 x 10 10 мм 3 x ––––––– = 5,94 x 10 4 дм 3 (100 мм) 3 Обратите внимание на то, как 3 мм входит в знаменатель коэффициента преобразования, чтобы отменить 3 мм на преобразовываемом значении.
1 дм равен 100 мм, поэтому 1 дм 3 = (100 мм) 3 = 10 6 мм 3
Обратите внимание, как 1 соответствует дм 3 , большему из единиц, когда по сравнению с 1 мм 3 .
5,94 x 10 4 дм 3 = 5,94 x 10 4 л, потому что 1 дм 3 равен 1 л
Пример № 6: Металлический куб со стороной 2,50 см. Рассчитайте объем в м 3 .
Решение:
1) Преобразовать 2,50 см в метры:
(2,50 см) (1 м / 100 см) = 0,0250 м
2) Умножьте, чтобы получить объем куба:
(0,0250 м) (0.0250 м) (0,0250 м) = 1,56 x 10 ¯ 5 м 3 (до трех сигнатур)
3) Вот альтернативный путь решения:
(2,50 см) (2,50 см) (2,50 см) = 15,625 см 3(15,625 см 3 ) (1 м / 100 см) 3 = 15,625 x 10 ¯ 6 м 3
15,625 x 10 ¯ 6 м 3 = 1,56 x 10 ¯ 5 м 3 (до трех сигнатур)
Пример 7: Преобразовать 10.6 кг / м 3 г / см 3
Раствор:
1) Сначала выполните некубическое преобразование, преобразуйте кг в г:
10 3 г 10,6 кг / м 3 x ––––– = 1,06 x 10 4 г / м 3 1 кг Обратите внимание на использование в ответе экспоненциальной записи.
2) Далее выполните преобразование кубов, преобразуйте кубические метры в кубические сантиметры:
(1 м) 3 1,06 x 10 4 г / м 3 x ––––––– = 1,06 x 10 ¯ 2 г / см 3 (100 см) 3 Обратите внимание, что 100 в кубе равно 10 6 .Вы можете записать 100 кубов в преобразовании как (10 2 ) 3
Вы также можете записать ответ как 0,0106 г / см 3 .
3) Убедитесь, что у вас все в нужном месте. Когда я отформатировал эту задачу, я сделал это около 7:30 утра в дождливую субботу. У меня был обратный коэффициент преобразования для кубического преобразования. Нужен МОАР КОФЕ !!
Пример 8: Преобразование плотности алюминия (2.70 г / см 3 ) до кг / м 3 .
Решение:
1) Вот план:
(a) преобразовать г / см 3 в г / м 3 (первый коэффициент преобразования на шаге чуть ниже)(b) преобразовать г / м 3 в кг / м 3 (второй коэффициент преобразования в шаге чуть ниже)
2) Небольшой анализ размеров:
(10 2 см) 3 1 кг 2.70 г / см 3 x ––––––– х ––––––– = 2,70 x 10 3 кг / м 3 (1 м) 3 1000 г
Пример № 9: Преобразование 409 кубических дюймов в литры с помощью анализа размеров.
Решение:
1) Вот план:
(а) преобразовать в 3 в см 3(б) преобразовать в см 3 в мл
(c) преобразовать мл в л
2) Вот настройка:
(2.54 см) 3 1 мл 1 л 409 дюймов 3 x –––––––––– х ––––– х ––––––– = 6,70 л (1 дюйм) 3 1 см 3 1000 мл
3) Комментарии:
(a) представьте, что 1 из 3 представляет собой куб размером один дюйм на дюйм на один дюйм.Поскольку 1 дюйм равен 2,54 см, один кубический дюйм равен кубу 2,54 см на 2,54 см на 2,54 см.(б) 1 см 3 = 1 мл — очень удобное преобразование, которое нужно запомнить.
(c) У Брайана Уилсона есть комментарий относительно числа 409.
Пример № 10: Если у куба со стороной 25,2 мм, каков его объем в литрах?
Решение:
1) Преобразовать 25,2 мм в см:
(25,2 мм) (1 см / 10 мм) = 2,52 см
2) Определите объем куба:
(2.52 см) (2,52 см) (2,52 см) = 16,003 см 3
3) Преобразовать в см 3 в мл:
(16,003 см 3 ) (1 мл / 1 см 3 ) = 16,003 мл
4) Перевести мл в л:
(16,003 мл) (1 л / 1000 мл) = 0,0160 л
Бонусный пример №1: Моль любого идеального газа в STP занимает 22,414 л. Сколько молекул газообразного водорода содержится в 22,414 мм 3 ?
Решение:
1) Я собираюсь построить решение для размерного анализа, по одному фактору за раз.Сначала сформулируем информацию о проблеме:
1 моль ––––––– х 22,414 л Я намеренно поставил это значение таким образом, потому что знаю, что окончательный ответ будет некоторым количеством молекул на кубический миллиметр. Объем должен быть в знаменателе.
2) Надо избавиться от литров и перейти к какому-то кубическому измерению:
1 моль 1 л ––––––– х ––––– х 22.414 л 1 дм 3 Зная 1 L = 1 дм 3 — удобное преобразование, которое нужно запомнить.
3) Теперь конвертируем из кубических дециметров в кубические миллиметры:
1 моль 1 л 1 дм 3 ––––––– х ––––– х –––––––– х 22.414 л 1 дм 3 100 3 мм 3 для этого:
100 3 мм 3Помните, что в 1 дм 100 мм, поэтому есть:
100 мм x 100 мм x 100 мм в одном дм 3
4) Последнее преобразование из молей в молекулы:
1 моль 1 л 1 дм 3 6.022 x 10 23 молекул ––––––– х ––––– х –––––––– х –––––––––––––––––––– = 2,687 x 10 16 молекул (до 4 сигн.) 22,414 л 1 дм 3 100 3 мм 3 1 моль
Пример бонуса 2: Металлический куб имеет следующие размеры: ширина 5.20 дюймов, длина 6,00 см и высота 1,00 фарлонг. Какой объем куба в кубометрах? В кубических ярдах?
Решение:
1) Преобразуем каждое измерение в метры. Все, что нам нужно сделать, это умножить вместе, чтобы получить кубические метры:
(5,20 дюйма) (1 м / 39,3701 дюйма) = 0,13208 м
(6,00 см) (1 м / 100 см) = 0,0600 м
2) Ферлонг более активен:
220 ярд 3 футов 12 дюймов 2.54 см 1 метр 1,00 фарлонг х ––––––– х ––––––– х ––––––– х ––––––– х ––––––– = 201,168 м 1 фарлонг 1 ярд 1 фут 1 дюйм 100 см
3) Напоминаем, что нужно быть осторожным.Когда я настраивал преобразование фарлонга в метры, я поменял местами 2,54 и 1. Я знаю это достаточно хорошо и все еще становлюсь жертвой случайной ошибки. Проверьте свою работу! Вот объем в кубометрах:
(0,13208 м) (0,0600 м) (201,168 м) = 1,59 м 3 (до трех сигнатур)
4) Преобразуйте кубические метры в кубические футы:
(1,594216 м 3 ) (39,3701 дюйм / м) 3 (1 фут / 12 дюймов) 3 = 56,3 футов 3 (до трех сигнатур)Обратите внимание, что я использовал значение кубического метра с несколькими дополнительными цифрами, а не округленное значение 1.59.
Проб 1-10
Вернуться в меню метрической системы
Квадратных футов в кубические футы Калькулятор
Как перевести квадратные футы в кубические футы?
Прежде чем мы обсудим, как выполнить этот расчет, важно отметить, что квадратный фут — это единица площади (два измерения), а кубический фут — это единица объема (три измерения). Итак, это не преобразование как таковое, поскольку мы не сравниваем как для подобного.
Стоит знать, что у нас есть отдельный калькулятор для расчета кубических ярдов из квадратных футов.А если вам это нужно, у нас есть статья о том, как рассчитать квадратные метры от стандартные измерения длины и ширины.
Чтобы рассчитать кубические футы на основе числа квадратных футов, нам необходимо знать дополнительное измерение: высоту / глубину. Теоретически вы могли бы вместить множество квадратных футов в кубический фут. Представьте себе бассейн — он может быть очень длинным, широким и мелким. Или он мог быть короче по длине и ширине и быть очень глубоким. Оба этих бассейна могли, теоретически имеют такой же объем в кубических футах.Но их площадь поверхности была бы совсем другой. Вот пример двух коробок, каждая размером 6 кубических футов.
Причины, по которым вы хотите рассчитать кубические футы из числа в квадратных футах, могут быть разными. Одна из частых причин — ландшафтный дизайн. Возможно, вы захотите купить мульчу или верхний слой почвы для своего сада — обычно эти материалы продается в кубических футах. Предположим, вы знаете, сколько квадратных футов занимает ваш сад, теперь вам нужно определить, сколько кубических футов верхнего слоя почвы вам понадобится.Вот что нам нужно знать:
Примечание: в этих формулах предполагается, что все измерения находятся в футах .
Формула для кубических футов
Кубические футы = ширина × длина × высота (или глубина)
Квадратные футы в кубические футы
Кубические футы = квадратные футы × высота (или глубина)
Пример
Допустим, у вас есть сад площадью 20 квадратных футов, и вы хотите покрыть его 3-дюймовым слоем верхнего слоя почвы.Требуемый верхний слой почвы продается в кубических футах, поэтому нам необходимо произвести пересчет и расчет.
- Преобразуйте нашу глубину из дюймов в футы (чтобы единицы были одинаковыми). В футе 12 дюймов. 3 ÷ 12 = 0,25 фута
Глубина нашего верхнего слоя почвы составляет 0,25 фута - Кубические футы = квадратные футы × глубина.
Итак: 20 × 0,25 = 5. - У нас общее количество: 5 кубических футов .
Как перевести кубические футы в квадратные?
Как мы обсуждали выше, важно отметить, что это не преобразование, поскольку кубический фут — это единица объема (трех измерений), а квадратный фут — это единица площади (двух измерений).Итак, вы не сравниваете как для подобного. Чтобы вычислить, сколько квадратных футов площади в ваших кубических футах объема, вам нужно знать одно из измерений. В нашем калькуляторе выше мы указали это как «рост», но в равной степени это может быть длина или ширина, в зависимости от того, с какой стороны объекта вы пытаетесь измерить. Как только у вас будет одно из измерений, ваши расчеты могут быть выполнены по формулам, приведенным ниже.
Примечание: в этих формулах предполагается, что все измерения находятся в футах .